仍以图形D为例，从表1.1知，图形D的原观测向量和再生观测向量分别是:

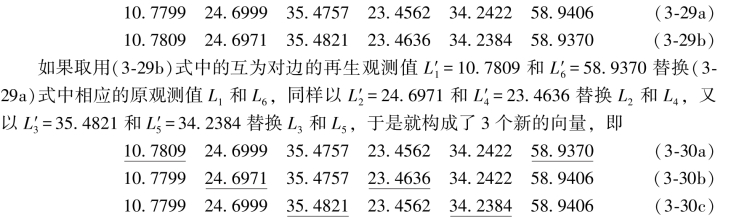
在以上各向量中都是具有2个再生观测值和4个原观测值，以后就称这样的观测向量为“混合观测向量”。除此之外，还可从(3-29a)式中取用互为对边的原观测值替换(3-29b)式中相应的再生观测值，于是又构成了3个新的向量如下:

在以上各向量中都是具有2个原观测值和4个再生观测值，其中是以再生观测值为主，故称之为“混合再生观测向量”，或简称为“混合再生向量”，相应地，将(3-30)式各式简称为“混合向量”。

以上两种情况可以概括地表达为:

由(3-33a)式和(3-33b)式分别列出它们的单环条件方程如下:

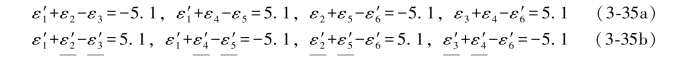
同样地，由(3-31a)式即(L1，L6)的混合再生向量以及由它计算出来的再生向量分别是:

将(3-36b)式中的再生向量和(3-29b)式中的再生向量相对比即可看出，由(L1，L6)的混合再生向量(3-36a)所求得的再生向量，其中每个再生观测值都互不相等，所以(3-36b)和(3-29b)中各相应再生观测值的真误差也就互不相同了。

考虑到(3-36a)式是(L1，L6)的混合再生向量，(3-36b)式是(L1，L6)的二次再生向量，就可以写出该两式的矩阵表达式，以及它们所对应的真误差矩阵式应如下式所示:

1.误差距的真误差置换法

于是，由(3-39a)和(3-39b)两式得:

于是，由(3-41a)和(3-41b)两式得:

(3-42)式就是由(L1，L6)的混合再生向量((3-36a)式)列出的第1、3两个单环条件(见(3-38a)式)。(3-35b)式是由(3-33b)式列出的单环条件，因为(3-33b)式是由(3-33a)式计算出来的再生条件，所以由该式列出的条件，其闭合差总是和由(3-33a)式列出的数值相等，正负相反。同样地，(3-38b)中的条件方程，其闭合差和(3-38a)中的数值相等，正负相反，这是因为(3-38b)是由(3-36b)式列出的条件，而该式则是由(3-36a)式求得的再生向量。

2.综合误差展开法

(3-43b)式括号中的(-ε2+ε3+ε4-ε5)，由表1.1知实际上就是图形D中无1、6的双环条件，其闭合差等于10.2，因此，由(3-43b)式得

类似地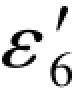，＝-0.5(6)＝-0.5(-ε2-ε5-ε3-ε4)＝0.5(ε2+ε5)+0.5(ε3+ε4)(3-44a)

将(3-44a)式代入ε3+ε4-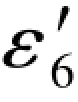＝5.1中，则有

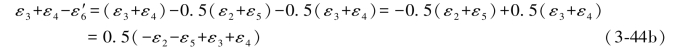
(3-44b)式括号中的数值仍然是图形D中无1、6的双环条件，其闭合差等于10.2(表1.1)，于是得

(3-45a)式和(3-45b)式以及它们真误差的矩阵式应为:

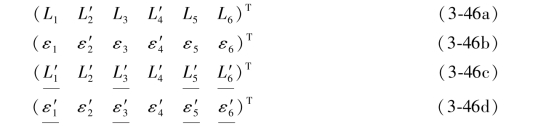
由(3-45a)式中的混合向量以及由(3-45b)式中的一次再生向量分别列出的单环条件应为:(www.daowen.com)

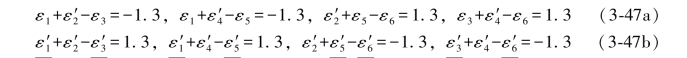
上述(3-47a)式中的闭合差都是等于1.3或-1.3，同样可以采用误差距的真误差置换法或综合误差展开法对此加以证明。为了节省篇幅，现在采用误差距的真误差置换法对(3-47a)式中的第2个条件加以证明。在(3-45a)式中如果不用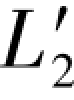和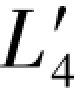而是换成原观测值L2和L4。那么，它实际上就是(3-29a)式中的原观测向量，由该向量列出的第2个单环条件应为:ε1+ε4-ε5＝6.1，由表1.1知误差距Δε4＝-7.4，若利用Δε4进行真误差置换，则可写出:

于是，得

上式就是(3-47a)式中第2个单环条件。

因为(3-45b)式是由(3-45a)式计算而得的再生向量，所以由(3-45b)式列出的条件，即(3-47b)式，其闭合差必然与由(3-45a)式列出的数值相等，正负相反。

(3-31b)式是(L2，L4)的混合再生向量，由它计算出来的再生向量也就是(L2，L4)的二次再生向量，它们分别是:

(3-49a)式和(3-49b)式以及它们真误差的矩阵表达式应为:

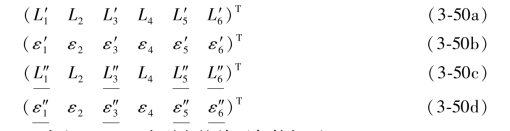
于是，就可以写出由(3-49a)式和(3-49b)式列出的单环条件如下:

于是，有

(3-51b)式是由(L2，L4)的二次再生向量列出的条件，该式是由(L2，L4)的混合再生向量即(3-49a)式计算出来的再生向量，所以(3-51b)式与(3-51a)式中的条件方程，其闭合差数值相等，正负相反。

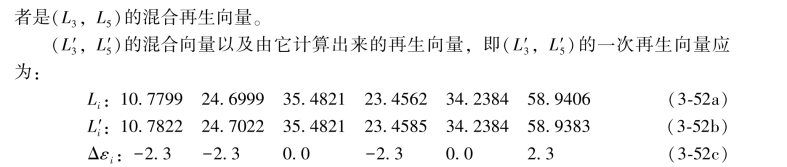
(3-52a)式、(3-52b)式以及它们的真误差矩阵表达式应为:

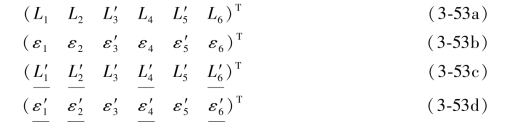
由(3-52a)式以及由(3-52b)式列出的单环条件分别为:

由(3-31c)式，即(L3，L5)的混合再生向量以及由该向量计算出来的再生向量，即(L3，L5)的二次再生向量，应如下所示:

(3-55a)式是(L3，L5)的混合再生向量，(3-55b)式是(L3，L5)的二次再生向量。这两个向量以及它们真误差的矩阵表达式应为:

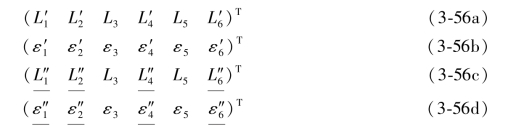
对照上述符号，即可写出(3-55a)以及(3-55b)两式的单环条件分别为:

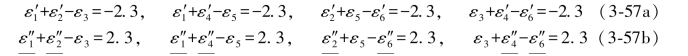
(3-55b)式是由(3-55a)式计算出来的再生向量，所以由该式列出的条件方程(3-57b)式和由(3-55a)式列出的，其闭合差应数值相等，正负相反，以上所有条件闭合差均等于2.3或-2.3。现在采用误差距的真误差置换法证明(3-57a)式中的第1、3两个条件。

从表1.1可以查到Δε1＝-1.0，Δε2＝2.8，Δε6＝3.6，于是有

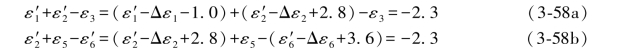
式中，

由表1.1知，由图形D的原观测向量列出的第1、3两个单环条件，应为ε1+ε2-ε3＝-4.1和ε2+ε5-ε6＝-1.5。这说明(3-59a)和(3-59b)两式的推导是正确的。

从以上所有推导可以得到如下几点结论:

前面所提出的一次再生向量和二次再生向量，将在第6章中得到应用，这里就不再多加叙述了。