由表1.1知，图形D的再生双差和方程为:

由(2-15)式可知，

将(2-15)式中的第1个式子代入(2-23)式中的第1个式子，则有

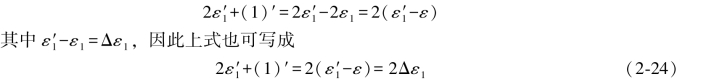
同理，可以由(2-23)式得到如下6个等式:

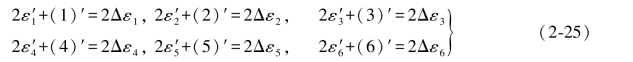
由此可以得出结论，即再生双差和方程等于其两倍的误差距。由于原双差和方程与再生双差和方程常数项相等，而正负相反，所以原双差和方程应等于误差距负的两倍。于是可以写出以下两个式子:

同样，还可以算出以下数值:

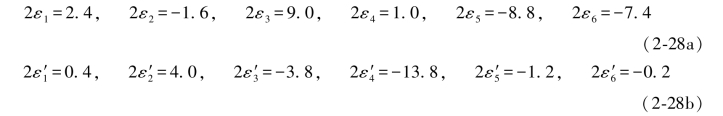(www.daowen.com)

将以上数值代入双差和方程，则得

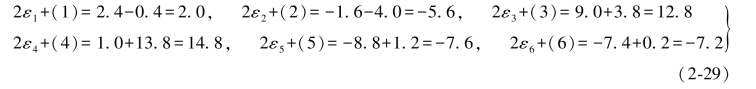
以上6个结果实际上就是表1.1中6个双差和方程，只不过表1.1中的结果是通过两个单环条件方程相加而得的，而上述结果则是通过实际的εi和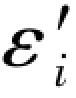按综合误差公式计算以及2εi或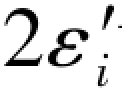计算而得。

再将(2-27b)式和(2-28b)式中数值代入再生双差和方程，又可得到:

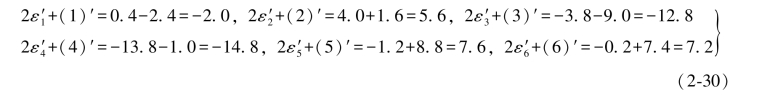
以上6个结果也和表1.1中6个再生双差和方程相一致。

也就是说，在交叉线的两端，其数值相等而正负相反。因此，任何一个双差和方程和它的再生双差和方程都是具如图2.1所示的图解关系。

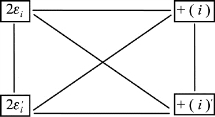
图2.1

实际上，上述图解也就是(2-14)式和(2-15)式的另一种表达形式，因为这一图形类似于一个“大地四边形”，因此称它为双差和方程与再生双差和方程之间的“大地四边形规律”。