以上两式还可写成:

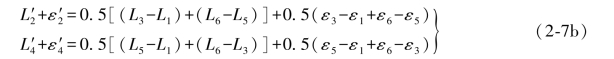
由(2-7b)式减去(2-5)式，则有

将(2-8a)式等号右边与表1.2中综合误差公式相比较，即知(-ε1+ε3-ε5+ε6)＝-(2)和(-ε1+ε5-ε3+ε6)＝-(4)，于是得

因此，无需更多推证即可写出如下6个公式:

根据原观测向量与再生观测向量的可交换性，又可由(2-9)式直接写出如下6个公式:

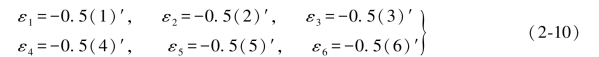
由(2-10)式可以得到结论:任何一个再生观测值的综合误差乘以-0.5就等于其原观测值的真误差εi(i＝1，2…，6)；也可以说，任何一个原观测值的真误差εi等于其再生观测值综合误差(i)＇的二分之一并反号。

以上两组公式(2-9)和(2-10)可以简写成:

(2-9)和(2-10)两式中的公式，统称为“真误差与综合误差的换算公式”。这两组公式很有实用价值，在以后将常常会用到。为了往后查阅方便起见，现将图形D的有关公式列入表2.1，同时将综合误差公式(表1.2)同时也写入表2.1中，主要是为了应用起来比较方便。

表2.1　图形D真误差与综合误差换算公式

(www.daowen.com)

由以上数据即可求得:

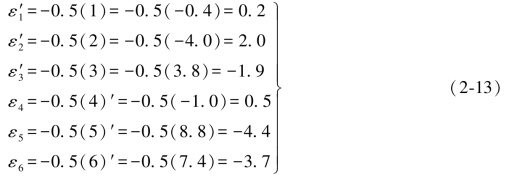
这里需要指出的是，上述计算结果只是表明前面导出的真误差与综合误差的换算公式是正确的，但是表1.1中的εi和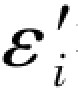都是根据高差真值和观测值计算出来的，在高差真值还没有求出之前，这些真误差事实上都是未知的，而求真法的最终目的就是要求得各高差的真值或真误差。

由(2-9)式和(2-10)式，又可写出如下两组公式:

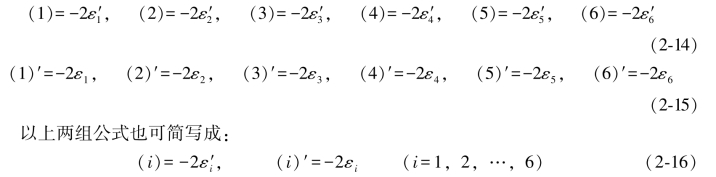
下面将分别对图形F和图形H的数据进行计算，以便进一步证实前面所导公式的正确性和可靠性。

[例题1续1]　现将适用于图形F的真误差与综合误差换算公式列在表2.2内，为了往后查阅和应用方便起见，并将表1.4中的综合误差公式也一并列入表2.2内。

表2.2　图形F真误差与综合误差换算公式

将以上数据代入换算公式得:

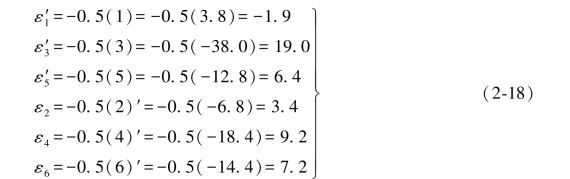
以上所有结果与表1.4中的数据完全一致。

将以上数据代入换算公式，得:

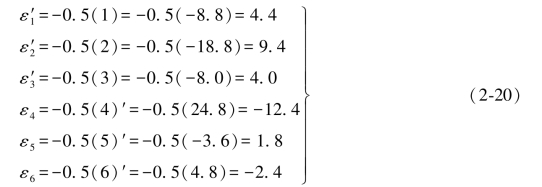
上述结果与表1.7中的数值完全一致。