在典型图形D中可以列出4个单环条件(见(1-7)式)，前文已指出，同一个真误差εi(i＝1，2，…，6)在这4个条件中都是先后出现两次。现在如果将同一个误差所在的两个条件相加，即可得到另一个新的方程。需要指出的是，有的真误差在两个条件中的前置符号不同，例如，ε3在第1条件中其符号为负，而在第4条件中其符号为正，如果将这两个条件直接相加，将使ε3正负抵消，在这种情况下，必须将第1条件等号两边同时改变正负号，然后再与第4条件相加。按照这一做法，于是得到6个相加的结果为:

如果令:

则(1-17)式即可写成如下形式:

这里需要指出两点:

①在互为对边的两个综合误差中，如在(1)和(6)中，它们都不包含ε1和ε6；在(2)和(4)中都不包含ε2和ε4，在(3)和(5)中都不包含ε3和ε5，也就是说，在互为对边的两个综合误差中，它们既没有它本身的真误差，也没有它对边的真误差。

②综合误差公式(1-18)是随典型图形的图形结构而定。(1-18)式是根据图形D(见图1.2)导出的，只要图形未变(指6个箭头方向未变)，则综合误差公式保持不变。图形F(见图1.1)则另有适合于它的综合误差公式，这些公式将在后面的例题1中给出，同样，适合于图形H的综合误差公式将在后面的例题2中给出。(www.daowen.com)

综合误差公式(1-18)式也可以按对边分组的形式书写，即

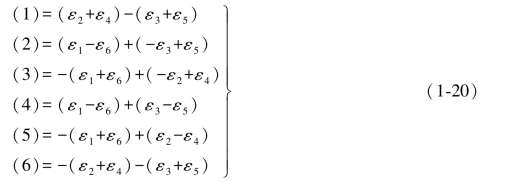
在(1-14)式中已经写出了图形D的4个再生单环条件方程。前面已经提过，用再生观测值所列出的条件方程，其闭合差和由原观测值列出的是数值相等，仅仅正负相反。因此，如果现在用(1-14)式中的再生单环条件仿照(1-17)式中的做法，则同样可以得到6个再生双差和方程如下:

很显然，它和(1-19)式中的双差和方程相比，只是常数项的正负相反，而数值相等。式中，(i)＇称为“再生综合误差”，它们的具体形式则可对照(1-18)式直接写出:

其对边分组形式则可对照(1-20)式直接写出: