通过模拟已经有了图形D(图1.2)的6个高差观测值为:

对照图1.2，可以列出1个外环条件(ABC)和3个内环条件(ABD、BCD、ACD)如下:

在以上4个条件中的第一项分别是ε1、ε1、ε2、ε3，它们的前置符号均要求为正，也就是说，在列这4个条件时，前3个条件是以ε1、ε2和ε3的箭头指向，即按顺时针方向列出的，而在列第4个条件时则是沿着ε3的箭头指向即逆时针方向列出的。这样，就可以保证这4个条件的第1项前置符号都是正号，而不会出现负号。以后将(1-7)式中的4个条件依次称为第一条件、第二条件、第三条件和第四条件。在这些条件中都是包含了三个真误差，以后称这种条件方程为“单环条件方程”。对于任何一个典型图形，这4个单环条件都要求按相同顺序排列，即外环条件作为第一条件，然后是3个内环条件，其第一项分别是ε1、ε2、ε3，且要求它们的前置符号均为正。

在4个单环条件中，每个真误差εi(i＝1，2，…，6)都先后出现两次，例如，ε1出现在第一、二两个条件中，ε2出现在第一、三两个条件中……ε6出现在第三、四条件中，等等。在第一条件中，除了ε1还有ε2和ε3，因此称(ε2，ε3)为ε1的“第一伴随误差对”，同样，在第二条件中，除了ε1还有ε4和ε5，因此称(ε4，ε5)为ε1的“第二伴随误差对”。由于每个误差在4个条件中都出现了两次，所以每个误差都有两个伴随误差对。根据这一定义并对照(1-7)式即可写出6个误差的伴随误差对为:

与伴随误差相对应的观测值称为伴随观测值。例如，L2、L3、L4、L5是L1和L6的伴随观测值，L1、L3、L5、L6是L2和L4的伴随观测值，L1、L2、L4、L6是L3和L5的伴随观测值。在图1.2中除了可以列出4个单环条件之外，还可以列出如下3个条件方程(图1.3)，即

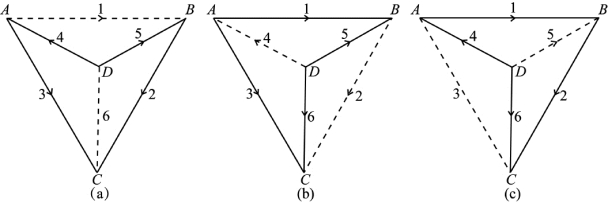
图1.3

以上3个条件的特点是，每个条件都含有4个真误差，从图1.3可以看出，每个条件都跨过两个水准环，所以称这3个条件为“双环条件方程”。

在一个典型图形中有6条水准路线，这6条路线可以分成3组，即线路1和6，2和4，3和5。线路1和线路6互称为对边，即1是6的对边，6是1的对边。同样，2和4，3和5都是互为对边，所以在一个典型图形中总是有3组对边。从(1-9)式可以看出，其中第一个条件中没有ε1和ε6，在第二个条件中没有ε2和ε4，在第三个条件中没有ε3和ε5，换言之，在每个双环条件中只包含两组对边，所以这3个条件也可以按对边分组的形式写出，即

用对边分组的形式书写双环条件方程，就可以很容易看出该条件中缺少了哪一组对边。因为在上述第一个条件中没有ε1和ε6，所以称该条件为“无1、6的双环条件”，同样，称第二和第三条件为“无2、4的双环条件”和“无3、5的双环条件”。

这里需要指出的是，对于双环条件并不要求第一项的前置符号一定为正，所以每个双环条件既可以顺时针列立，也可以逆时针列立，因此对于每个双环条件，总是有两个数值相等而正负相反的闭合差。这两个闭合差在以后都可能用到。

此外需要指出的是，在最小二乘平差中，对于图1.2中的水准网而言，只能选用3个线性无关的条件方程或者说彼此独立的条件方程，而在上面已经列出了4个单环条件和3个双环条件，显然是不能同时采用的。但是在求真法中情况完全不同，在求真法中是要利用有限的6个观测值构成不同形式的观测向量和尽可能多的函数，从而利用这些向量和函数值来求解我们所需要的真误差和真值。因此，在求真法中无需考虑条件是否独立的问题。(www.daowen.com)

在每个典型图形中，除了6个是通过水准测量在野外获取的高差观测值之外，从图1.2中不难看出，每个高差还可以通过两条不同路线推算出它的高差值。例如，第1条线路，除了直接测得的高差观测值L1＝10.7799m之外(见(1-5a)式)，还可以经过线路3和2推算出它的高差值，即L3-L2＝35.4757-24.6999＝10.7758m，另外，还可以经过线路4、5又推出它的另一个高差值为L5-L4＝34.2422-23.4562＝10.7860m，取平均后得到线路1的另一高差值为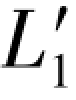＝0.5[(L3-L2)+(L5-L4)]＝0.5(10.7758+10.7860)＝10.7809m。同样，对于其余5个线路也都可以仿此进行推算。对照图1.2即可写出6个推算公式为:

(i＝1，2，…，6)称为第i条线路的再生观测值，它的真误差则用符号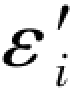来表示。为了避免混淆，以后将每条线路上的直接观测值Li称为“原观测值”，它的误差εi则称为“原误差”。有时在不致混淆的情况下，也可以不加“原”字。

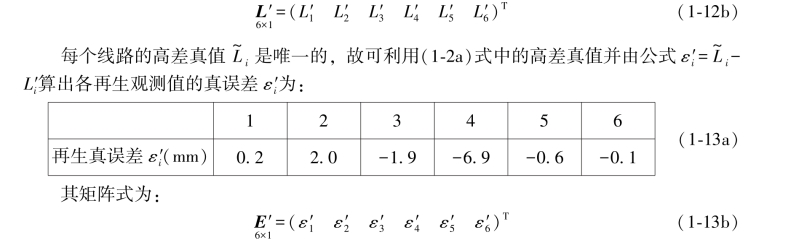
将(1-6)式的原观测值分别代入(1-11)式，即可算出6个再生观测值为:

它的矩阵式为:

到现在对于每条水准线路来说已经有了两个高差观测值，即一个是原观测值Li，另一个是再生观测值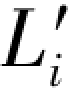。现将两套观测值分别标注在图1.4(a)、(b)上。

利用再生观测值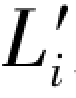又可以列出4个再生单环条件方程:

以及3个再生双环条件方程:

以上3个条件也可按对边分组的形式书写，即

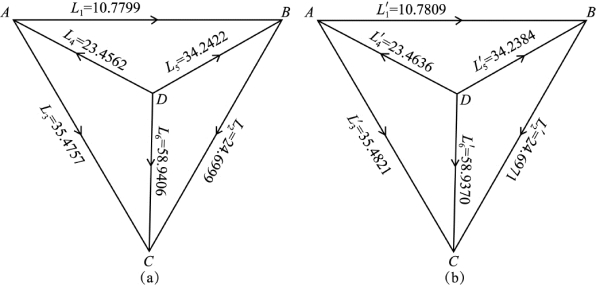
图1.4

这里顺便指出，用原观测值和再生观测值列出的所有条件方程，它们的闭合差都是数值相等，而正负相反。这是一种必然的结果，并非巧合，其原因将在下章予以证明。另外还要指出的是，每一个典型图形的3个双环条件，其闭合差只与观测值有关，观测值确定以后，3个闭合差的数值也就固定不变了，例如，对于图形D而言，3个闭合差分别是-10.2、-2.6和4.6并各有正有负。图形F和图形H则另有不同的3个闭合差值。