在求真法中是采用中点三边形的水准网作为建网的基本图形，由一系列基本图形相邻接或部分重叠，从而形成一个整体的网形，覆盖整个测区，在图1.1中是表示以F、D、H为中心的3个基本图形相邻接而成的一个水准网。

图1.1

为了阐述求真法的原理和推导公式，必须先模拟一套数据，通过这些数据来说明求真法的思路，并在导出一系列公式和算法之后，再用这些数据来验证求真法的立论是否正确，所导出的公式和算法是否可靠，因此，在对求真法进行研究时，模拟数据是不可或缺的。模拟数据应包括:基本图形中4个水准点的高程值，6条水准路线的高差真值，高差的真误差，高差的观测值等。在图1.1的下方是网中8个水准点模拟的高程真值，这些数值可以任意给定，没有任何限制。

在本书中将图1.1中以D为中心的基本图形作为一个范例，自始至终都是围绕这一范例来阐述求真法的原理并推导其公式。为了验证求真法的原理和公式是否正确可靠，又取图1.1中以F、H为中心的两个基本图形作为例题，随着书中所给出的计算公式和方法进行实际运算。

为了使所导出的公式和方法能够普遍适用于所有的基本图形，于是对基本图形的某些方面提出了统一的规定。

①线路的编号。图1.2是取自图1.1以D为中心的基本图形。在以A、B、C三点连成的外环线的编号为1、2、3(顺时针方向)，其次在1、3线路之间编号为4，然后按顺时针依次编号为5、6。图1.1的3个基本图形编号都是符合这一规定的。

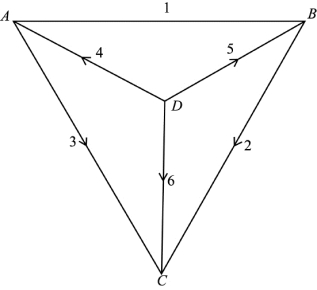
图1.2

②两个基本图形的公共边，其编号可以相同，也可以不同。例如，图1.1中的BC边编号均为2，而AC边的编号，在图形D中编号为3，而在图形F中编号则为1。为了便于区分，在图形F中，编号是写在方括号内，在图形H中是写在圆括号内(图1.1)。

由于对所有基本图形的编号都作了统一规定，所以在图形外围三条线路的编号都是1、2、3，而处于内部三个水准环的编号则分别是1、4、5，2、5、6和3、4、6。

③在列条件方程时，条件方程的先后顺序以及每个条件方程的书写形式也都提出了统一的要求，有关这方面的具体内容，将在后面再作详细的说明。

由于对线路的编号、条件方程的顺序以及条件方程的书写形式也都作了统一的规定，这样就可以使得某一个基本图形所导出的公式和结论具有普遍的适用性，因此，以后将符合上述规定的基本图形称为“典型图形”。

下面将以图1.2中图形D为例，说明设立模拟数据较为简便易行的方法和步骤。

第一步　在图1.1中已经给出了8个水准点的(假定的)高程真值，其中A、B、C、D四点的高程值分别为:(www.daowen.com)

第二步　根据点的高程，在图上标出箭头指向，箭头指向必须是由低点指向高点。之所以要作如此规定，主要是要保证6个高差值都是正值。这一点和最小二乘平差是有所不同的。在最小二乘平差中，箭头指向可以由低到高，也可以由高到低。如果是由高到低，则该线路上的高差值将为负值，而在求真法中是不允许出现负高差值的。

第三步　由给定的高程真值算出6个线路上的高差真值，并用符号i(i＝1，2，…，6)表示，计算结果如下:

高差真值的矩阵式为:

第四步　对每个高差真值设定一个真误差，一般以毫米(mm)为单位。假设的真误差可正可负，数值可大可小，不必要作任何刻意的安排，可以随意假定。真误差将以符号εi(i＝1，2，…，6)表示。例如，现在设定如下6个真误差值:

其矩阵式为:

第五步　根据高差真值和真误差计算各线路模拟的高差观测值，高差观测值用符号Li(i＝1，2，…，6)表示。在以后的叙述中，将始终采用以下的符号定义:

当然，实际的情况是，除了通过水准测量获取的6个高差观测值之外，其余的数据，如高差真值、真误差等，尽管是客观存在的，但都还是未知的。而求真法的理论和计算方法正是解决通过有限个数的观测值求出其真误差和高差真值的这一难题。

按照上述步骤模拟出一套数据，这种做法难免使人怀疑，这是不是在自己出题自己求解。为此，建议读者现在也按上述步骤模拟出一套数据，然后随着本书所介绍的计算方法逐步进行计算，以便验证最后解得的结果是否与模拟的数值相一致。