一、模型原理和计算方法

(一)窗概率配对方法

1.原理

考虑到降雨的随机变化,我们不妨假设雨强(R)及反射率(Z)为随机变量,若假设雨量计在降雨区的分布是随机的,通过观测,我们得到这些点的雷达反射率及雨量计的配对。由概率论的基本原理我们知道这样的事实:若雨强与反射率之间存在一定的关系,则只要已知雨强或反射率的分布函数,相应的反射率或雨强的分布就能确定；然而,这里我们要讨论的是上述问题的反问题,即已知雨强和反射率的概率分布函数,求这两个随机变量之间的关系。这样的问题一般不可得,但若知道所需要确定的函数类,则可以确定函数关系。事实上,由雷达气象方程,已知Z—R 关系:

因此,可以利用Z 与R 的概率分布来确定函数关系式中的系数A 与指数b。

2.算法

第一步:资料,给出一定时间,同一空间的雨强及反射率对R(i),Z(i),i=1,2,3,…,m(m 足够大)。

第二步:R(i)从大到小排序,并将R 的值分成若干区间,确定其在这些区间上的频率,即对于任一区间R0,Rr(R0＜Rr),其累积频率:

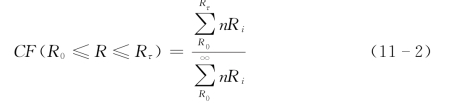
第三步:将Z(i)从大到小排序,即

第四步:考虑到系数A 和指数b 的变化范围,给出一组取值A0、b0假定:

第五步:利用A0、b0 及关系式(11-1)确定与R 划分的区间相对应的Z 的区间,根据第三步关于Z 的排序情况确定在不同区间上的频率,即相对于R0、Rr 区间的Z 的区间Z0,Zτ(Z0＜Zτ),其累积频率:

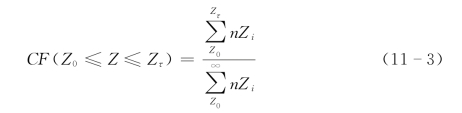
第六步:选择不同的参数A 和b,通过上述两种方法,即对观测值Z 的排序,和由雨强R 通过关系式(11-2)的转化得到的Z 的频率排序,使它们所得到的概率分布之偏差达到极小,即

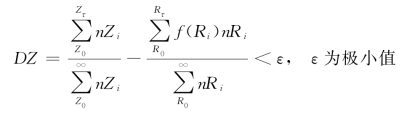
3.特点

算法通过分布来确定函数关系,对观测的误差不敏感,有别于简单地将Z 与R 分别排序后建立一一对应关系的最小二乘方法。最小二乘法要根据误差[Z-ARb]2 的大小来确定函数关系,它对于雨强大的点的观测误差极其敏感。事实上,该概率配对方法突出的是在整个降水区域的Z—R 关系。

4.缺点

该方法的缺点是,在计算Z—R 关系的过程中需要大量的历史资料进行配对得到一个经验的Z—R 关系,这对瞬时性降雨和特殊降雨过程可能会有一些偏差。事实上,如果我们能够对每一次降雨过程求得一个Z—R 关系则是最佳选择,但是由于每次雨量计资料的有限和该方法需要大量资料之间的矛盾,使得这种假设是不可能的,因此我们只有通过改进方法来解决。

(二)一种改进的最佳窗概率配对方法

1.原理

考虑到降雨的随机变化,我们不妨假设雨强及反射率为随机变量,若假设雨量计在降雨区的分布是随机的,通过观测,我们得到这些点的雷达反射率及雨量计的配对。事实上,由雷达方程,已知Z—R 关系类为:Z=ARb,从公式中我们能够看出,由于Z 与R 成指数关系,因此大的雨强对应大的dBz值,考虑到降水分布的随机性,我们考虑整个降水区Z、R 的分布也是随机的,因此可以将整个降水区观测到的Z、R 分别按大小排序,并以滑动窗的形式进行配对,然后通过最小二乘的拟合,由牛顿截弦法解出A 和b。

2.算法

第一步:利用每1h的实测资料配对(雷达和雨量计资料),运用概率论的方法进行运算得到一个实时的Z—R 关系。首先将观测到的雷达和雨量计资料配对分别按大小顺序排列起来:

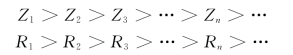
从左到右取滑动窗(滑动窗长为L),将 [Zmin,Zmax]划分为多个小窗[Z1,Zl],[Z2,Z1+l],…,[Zn-l+1,Zn]。同样对应的R 的窗为 [R1,Rl],[R2,R1+l],…,[Rn-l+1,Rn],分别求对应窗的滑动平均值Zk、Rk,得到一组对应的配对值。利用最优法可以得到一组配对的A 和b。

第二步:用上面求得的A 和b,通过Z—R 用已知的R 求出一组Z′k,将Z′k 按落在第一步中Zn 的各个滑动窗中进行分组并取出每一窗口内Z′k的最大值和最小值,用来和对应窗口Rn 的滑动窗中的最大最小值相对应,这将得到的一组新的Z、R 配对,再重复第一步的过程,通过最小二乘法算出一组更为精确的A 和b。

3.特点

由于Z—R 关系随降水类型在时空上不断变化,所以,用固定不变的Z—R 关系计算降雨量是不恰当的,因此最好根据实测得到的雨量资料,运用计算时随时建立的Z—R 关系式。该法不同于传统雨滴谱法建立的Z—R关系式,它是用雷达测得的雷达反射率因子Z 和雨量计实时测到的降雨量G,通过计算机直接进行快速计算和比较,最终建立最优化的Z—R 关系。该方法不同于传统的最优化方法,在传统的最优化方法中,仅仅是确定一个初始的Z—R 关系值,以及一个判定函数,通过逐步迭代的方法确定一个Z—R 关系使得判定函数达到最小值。这样计算出来的Z—R 关系对观测的误差非常敏感,特别是它对于雨强大的观测点的观测误差极其敏感,因此该方法在克服随机误差和系统误差方面比较差,因而得到的Z—R 关系往往和实际的Z—R 关系有较大的偏差。此外,传统的最优化方法在区域降水量测定中的精度与选取的区域大小有关,例如,选定一个大区域建立的Z—R 关系,对这个大区域来说是最优的,但是对于各个小区域来说就不一定是最优的,因此,该方法也有其空间的局限性。而对于窗概率配对方法,由于其需要大量的历史资料,因此传统的窗概率配对方法的实时性并不是太好。因此,我们在传统的最优化方法和概率配对法的基础上,充分利用两种方法的优缺点,作出了改进的最优窗概率配对法。如果对层状云和对流性降水分别计算Z—R 关系,对一小时的降水估测将会起到更好的作用。

4.缺点

由于每次实时计算都需要计算A、b参数,因此对观测资料的需要比较高,要求每次配对的资料达到一定的数目。另外在样本量较小的情况下,很容易受歧异数据影响。

(三)变分校正法

已知雷达降水场R(i,j)和雨量计观测场为存在雨量计的格点,订正因子

1.原理

在进行变分分析时,我们要求分析场R 必须满足:

(1)在每个网格点上订正因子之分析值CR(i,j)与观测场订正因子之间的偏差为最小,即CR(i,j)-~C~R(i,j)→min。

于是形成泛函极小问题

式中:α,ε为权重系数。

(2)其相应的Euler方程

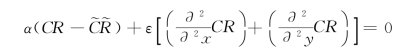
(3)迭代求解。

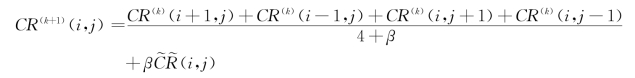
其中

(4)订正降雨场。在求得订正因子场后,便可以得到订正降雨场

2.特点

变分法考虑了降水的时空变化,从极值的观点使实际订正量与理论量更加接近一致。由于降水是随机变化的、非均匀的,校准量是时空的函数,变分校准法充分考虑了降水的这种特点,从时空意义上对雷达观测值进行校正,从而得到比较精确的结果。

3.缺点

用变分法校正时,要求雨量计分布达到一定的密度,并且要求雨量计的分布比较均匀,否则,得到的校正结果与实际相差较大。另外变分方法主要解决降水结构,因此最后能得到雨量计附近的梯度结构,这就决定了变分法的影响范围是有限的。

4.说明

在该方法中我们并没有用距离权重插值方法将测站的雨量计插入到网格上,这是因为取的网格比较细(2km×2km),在这样的分辨率下插值对计算精度的提高没有多大贡献。此外,由于雨量站比较稀疏(站与站之间的距离大于40km),如果插值也不会精确,所以,这里没有用到插值方法。

(四)卡尔曼滤波算法

1.原理

Kalman滤波的优点:在导出平均偏差场时,考虑了测量过程的噪声,同时避免了在计算Rg/Rr 比值时,因R 小造成的不稳定,提供了一个在计算偏差时估计误差的方法,以及由前一时刻的偏差估计和它的误差方差、现在的测量和测量误差方差的估计得到当前的偏差估计,预测下一个时刻的偏差。

2.算法

第一步:已知雷达测得的降雨场的时间序列以及相应时间,由雨量计得到降雨强度Rg(l,k,t),其(l,k)为空间坐标,t是时间。

第二步:计算观测偏差。

第三步:卡尔曼滤波方法的状态转移矩阵。

式中:k为离散时刻对应时间tk；ξk、ηk 为随机扰动项,可以假设为高斯白噪声序列。

第四步:卡尔曼滤波计算。

状态预测估计值公式:

预测估计值误差的方差公式:

其中

最佳增益公式:

状态估计值公式:

滤波误差的方差阵公式:

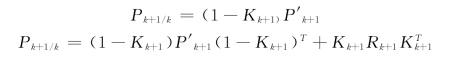
式中:Q、R 为常数(分别为Gauss白噪声ξk 和ηk 的方差)；Z∧k/k-1为由k-1时刻的平均偏差去估计k时刻的平均偏差所得的值。

第五步:订正降雨场。订正降雨场为

3.特点

因为雷达接收资料的误差是随机的,而Kalman滤波法得到的正是这个误差的校准因子,故在整个雷达的观察网上可以用来校准雷达值。但是Kalman滤波法又比平均校准法优越,因为它避免了求G/R 时,因R 过小而产生的不稳定(因为如果R 过小,如R＜0.1mm,则即使G 不太大,有可能使G/R 比较大,超过G/R 实际应该的大小,在这里,我们做了一些处理,即只处理降雨量R＞1mm,并且R/G＜5的资料配对),另外Kalman滤波法导致了测量过程中的噪声,滤除了有色噪声,因此效果较好。相反因为雨量计点是随机地散布在区域内效果才较好,否则将会产生噪声。

(五)平均校正法

1.原理

平均校正法的基本思想是认为雨量计观测降水是客观的,能代表一个区域的平均降水,可以利用雨量计的观测值来校正没有雨量计观测的区域。校正的方法是取某一个区域所有的雨量计观测降水的平均值Rg,以及由雷达回波得到的整个区域的降水初估场所计算得到的区域面平均降水量R0,计算两者的偏差然后利用这个偏差因子来校正每一网格的降水。

2.缺点

因为这种方法所求的是平均校准因子,所以会平滑掉降水分布场,从而平滑掉强弱回波中心,因此改变了降雨场的实际结构,不能真实的反映降水场结构。

(六)卡尔曼——变分联合校正(变分法确定卡尔曼滤波系数)

1.原理

Kalman滤波的优点:在导出平均偏差场时,考虑了测量过程中的噪声,同时避免了在计算Rg/Rr 比值时,因R 小造成的不稳定,提供了一个在计算偏差时估计误差的方法,以及由前一时刻的偏差估计和它的误差方差,及由现在的测量和测量误差方差的估计得到当前的偏差估计,预测下一个时刻的偏差。而变分校正的优点在于能够保持校正雨量计周围的降水结构,突出雨量场的分布。考虑到卡尔曼校正和变分校正的优缺点,我们可以先用卡尔曼滤波对整个范围的回波做校正,将得到的结果再进行一次变分校正从而得到最终结果。

2.算法

第一步:同卡尔曼滤波,计算出平均偏差场,校正后得到降雨场分布R(I,J)。

第二步:将第一步得到的结果再通过一次变分法校正,得到最终的降雨场(I,J)。

3.特点

既利用了卡尔曼滤波的优点,滤除了测量过程的噪声同时避免了在计算Rg/Rr 比值时,因R 小造成的不稳定,对整个范围的回波做了订正,又利用变分校准法充分考虑了降水随时空随机分布的特点,从时空意义上对雷达观测值进行再次校正,突出降水的结构,从而得到更为精确的结果。

4.缺点

由于变分法影响的范围同雨量计分布的密度和位置有关,特别是对离雨量计较远的地方变分法就显得无能为力了,因此卡尔曼变分联合校正在降水校正精度总体上有提高,但是在对离校正雨量计较远的位置,还是会使降水回波强弱中心平滑,不能真实的反映降水场结构。

(七)降雨量预报(交叉相关方法确定降雨量)

1.原理

把整幅图像上的回波作为一个整体来处理,并且假设全体回波形状和强度不变,并且具有一致的移动方向。方法是通过线性外推将第一时刻取得的回波图像的重心向任一方向移动一定的距离,然后计算此图像与第二时刻图像之间的交叉相关系数γ,然后再向另外一个方向移动一定距离,这样对不同的移动位置,会得到不同的相关系数,直到找到极大值γmax为止,该极大值的位置就是最优的回波中心位置。

2.算法

第一步:选择两幅资料(时间分别为t0 和t1),数据分别投影到m×n个网格点上 [表示为F(I,J,t0)和F(I,J,t1)],分别计算出各自的中心(It0,Jt0)、(It1,Jt1)。

第二步:给出ΔI、ΔJ,计算

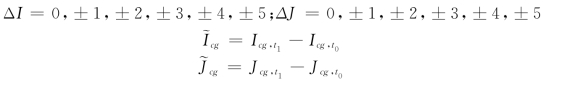
第三步:计算出F1(I,J,t0)与F2(I+~Icg+ΔI,J+~Jcg+ΔJ；t1)的hit矩阵。

第四步:求相应于F1 和F2 模式的有关统计量的值。

均值

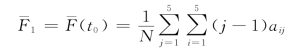
其中

方差

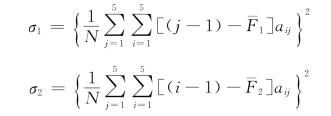
第五步:求交叉相关系数。计算交叉相关系数的分子。

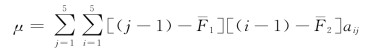
求交叉相关系数

从而形成交叉相关系数矩阵,从矩阵中取出最大值记为

第六步:计算雨量移动速度。

速度

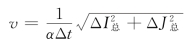
二、系统结构

1.系统逻辑结构

系统逻辑结构如图11-2、图11-3所示。

2.系统功能介绍

黄河三花间部分地区雷达信息面雨量估算和短时定量降水预报系统具备下述功能。

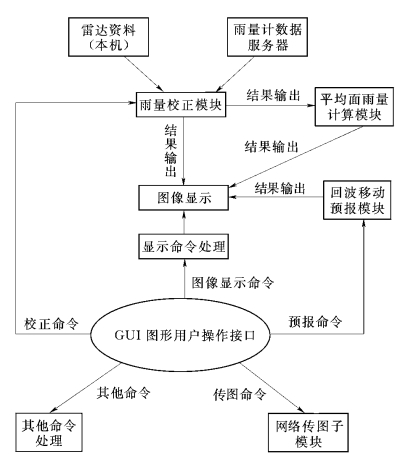
图11-2　降水处理系统结构图

(1)逐小时降水反演。按目前对三花间的分块情况,依据郑州714CD多普勒天气雷达1次/h的观测资料,制作黄河三花间部分地区过去1h分单元面雨量分布。

(2)时段降水量累积。依据上述分析成果,分单元进行过去3h、6h、12h累积降水量计算。

(3)1～3h临近降水预报。制作黄河三花间部分地区未来1～3h的定量降水预报。

本软件系统在以前的基础上作了算法和系统框架的改进,并增加了一些新功能:

(1)系统支持多平台(WindowsNT/2000等),系统稳定性更强。

(2)界面简洁、直观,便于用户操作和维护。如图11-4所示。

(3)可配置地图、调色板,可显示分类的地图信息和设置调色板。如图11-5所示。

(4)算法改进,新增加了卡尔曼滤波法、变分方法、平均校正法和窗概率配对方法的校正结果的显示和输出,预报人员可以根据实际观测情况选择相应的校正雨量作出洪水预报。

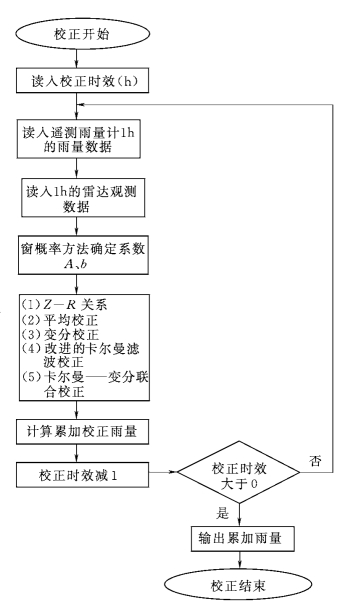
图11-3　校正计算运行流程图

(5)平均面降雨量显示功能。如图11-6所示。(www.daowen.com)

(6)增加了降水类型的选择,用户可以根据降水类型选择相应的雨量转换公式进行雨量估测,进一步提高校正精度。如图11-7所示。

(7)动画功能,使动画操作更直接、简便,可控制的参数也更多(如快进、快退、暂停、每秒动画帧数的设置)。如图11 8所示。

(8)局部放大功能,用户可以按任意倍数放大图像。如图11-9所示。

(9)增加了回波客观外推功能(即由交叉相关方法预报回波的移项移速)。如图11-10所示。

(10)增加了回波等值线功能。如图11-11所示。

(11)回波数字显示的功能,可以显示相应回波的选择区的数字信息。

(12)支持数据库的功能,支持多种数据库(Sybase、Access等),可以实时的通过数据库得到雨量计和雷达资料,提高了校正的实时性。

(13)增强了网络功能,用户可以直接通过软件进行实时图像传输。

(14)操作更加简便,增强了帮助功能,增加了帮助快捷方式,用户可以直接通过软件提供的帮助功能查找相应的操作说明。如图11-12所示。

三、关键技术和创新点

图11-4　系统界面

图11-5　调色板

早先人们提出的校正方法包括平均校准法、变分法和改进的变分法,但就我们所知这些方法都有不足之处,并且校正结果也不太理想。进入20 世纪80 年代,随着数理统计向应用性发展,人们进而认识到雷达测量所产生的误差本质——随机性,从而将卡尔曼滤波方法运用到降水分布场的测定上。另外,毫无疑问雷达观测存在系统误差,卡尔曼滤波不仅能够克服随机误差,也可以校正系统误差。但传统的卡尔曼滤波方法中的两个参数即雷达系统方差和观测方差是人为假定的两个常数,而实际观测中,这两个常数是随时间变化的,对不同的雷达—雨量计系统都是不同的。虽然国内外一些科学家对卡尔曼滤波作出了一些改进,但是到目前为止,这两个参数还是假定的。在工作中,对卡尔曼滤波方法进行更进一步的研究,主要是用数理方法利用观测到的资料直接解出了卡尔曼滤波的两个自适应系数,从而提高卡尔曼滤波的校正精度。

1.方法关键技术介绍

首先为了建立卡尔曼滤波器,必须建立数学模型,这个模型包含了两个部分,即:①平均场偏差模型；②雷达和雨量计的观察模型。

定义雷达——雨量计场的平均偏差为:

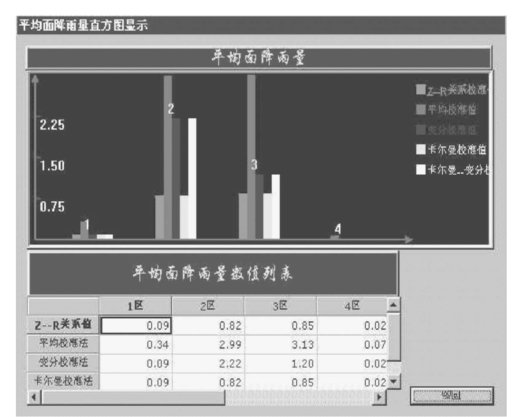
图11-6　各种校正方法得到的校正结果比较

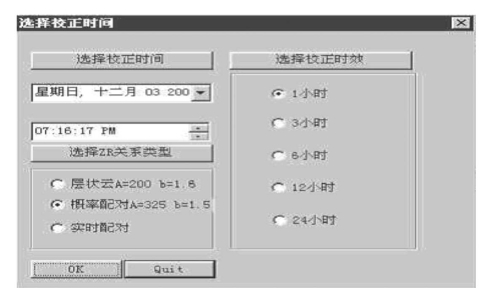
图11-7　校正时间

式中:GT 为真实的降雨场；|A|为雷达所能覆盖的降水区域面积；NR 为区域内非零雷达观测数目；Ri 为非零雷达观测值。

图11-8　设置动画

图11-9　放大图像

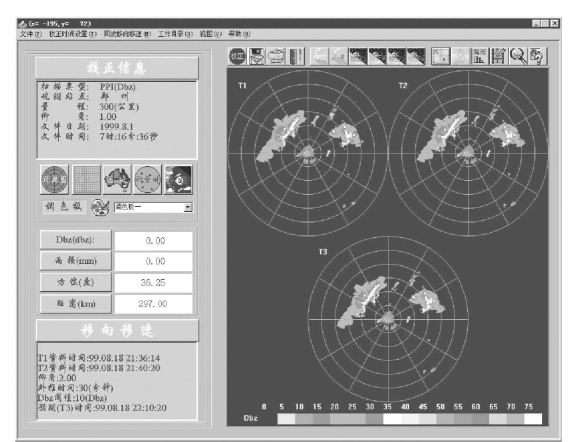
图1110　回波客观外推功能

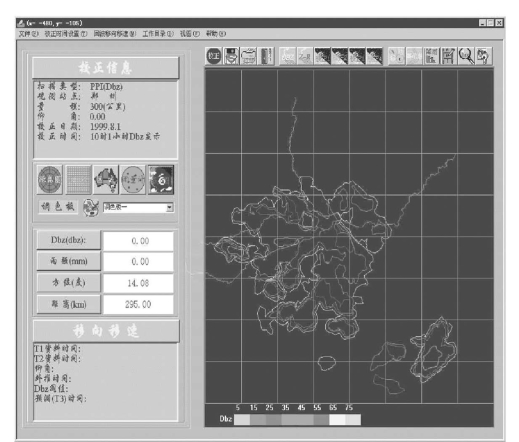
图11-11　回波等值线功能

图11-12　帮助对话框

因为从一个时刻到下一个时刻偏差的变化是随机的,即偏差的增大或减小是等可能的,所以我们假设偏差遵循下面的随机过程。

式中:{Bk}为k时刻雷达——雨量计场的平均偏差序列；{ωk}为一个均值为零,方差等于Q 的Gauss白噪声序列。

观测方程应该依赖于偏差、雷达和雨量计数据,三者之间有如下关系:

式中:{Zk}为观测偏差序列,定义为雨量计观察值之和比上相应的雷达值之和,即∑Gi(x,y)/∑Ri(x,y)[Ri(x,y)＞0]；{γk}为一个均值为零,方差等于R 的Gauss白噪声序列,并且假设{γk}和{ωk}相互独立。

由式(11-4)和式(11-5)构成卡尔曼滤波器所需要的数学模型。现在我们的目标是利用观测量Z0,Z1,…,Zk 去估计βk 的值。但是为了卡尔曼滤波器的运行,必须事先知道方差Q 和R 的值。为此,引进卡尔曼滤波理论中的“新息”序列:

在文献[15]中作者给出了一种计算参数的自适应方法,然而据我们所知,由于Pk/k-1 在计算R 时是未知的,所以并没有克服文献 [14]中的不足。这里我们在卡尔曼理论分析的基础上,提供了一个不需要人为假定的参数,而通过自身的计算来确定Q 和R。

式中: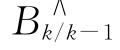是由k-1时刻的平均偏差去估计k 时刻的平均偏差所得的值；ek 为预测误差,等于Bk 减去。

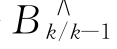由卡尔曼滤波模型,我们知道:

所以

利用关系式(11-5),得

假设我们知道{ωk}与{vk}是独立的,另外随机变量vk 与vk+1也是独立的,因此有

式中:D 为方差。

参数Q、R 为事先估计值,卡尔曼滤波方法通常假设

所以,以k-1时刻的偏差估计k时刻的偏差值为:

预测估计方差:

定义在卡尔曼滤波过程中所生成的新息序列:

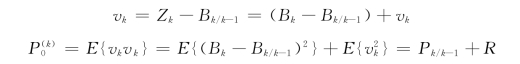
故有

同时,从卡尔曼滤波的理论分析,不难得到

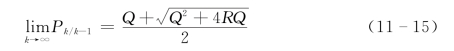
即有

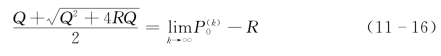
由式(11-7)得

联立式(11-10)、式(11-17)不难求得Q、R。

至此,我们求得了在卡尔曼滤波过程中所需的两个参数Q、R,下面我们给出卡尔曼滤波方程组。

状态预测估计值公式:

预测估计值误差的方差公式:

其中

最佳增益公式:

状态估计值公式:

滤波误差的方差阵公式:

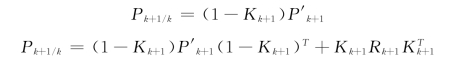
由卡尔曼滤波我们得到了k时刻雷达—雨量计的平均场偏差Bk 的估计值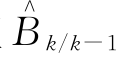,此时我们可以得到雷达观察的一次校正资料:

2.方法特点和创新

用这种改进了的卡尔曼滤波方法,不需要事先给定任何参数。计算过程中所需要的参数,均可以通过资料的累积给出,而且资料越多参数越精确。而且,采样的数据随时间的增长而增多,因此所求的统计量—偏差越趋向于分析值。

因为雷达接收资料的误差是随机的,而改进的卡尔曼滤波法得到的正是这个误差的校准因子,在整个雷达的观察网上可以用来校准雷达值。改进的卡尔曼滤波法又比卡尔曼滤波优越,因为它不需要人为的假定就可以计算每时刻卡尔曼滤波所需要的两个参数Q、R。同时它比平均校准法优越,因为它刚开始校正时需要的样本较多,但是一旦系统误差确定了,以后的样本就可以减少,可以适合小样本的情况。另外,改进的卡尔曼滤波法考虑了测量过程中的噪声,滤除了高斯白噪声(我们在以后的工作中将考虑滤除有色噪声的情况,对我们的算法作进一步改进),因此效果较好。相反,如果是用变分法的话则需要雨量计密度比较大,而且均匀分布,效果才会较好。

四、应用情况

1.集水区及遥测雨量计分布

将郑州714CD 多普勒天气雷达测量范围内的黄河流域水系划分为4个集水区,并将雨量计的经纬度位置转化成直角坐标的位置。

表11-2为4个集水区和雨量计密度个数。在本次实验中降水量比较集中在第一区和第二区。在今年的实验中遥测雨量计10min发出一个测量记录,但我们在定量测量降水中还是以1h为单位进行雨量校正,并以此作为雷达定量测量降水偏差调整的依据和实验标准。图11-13为黄河流域集水区和遥测雨量计位置。

表11-2　各集水区面积和遥测雨量计个数

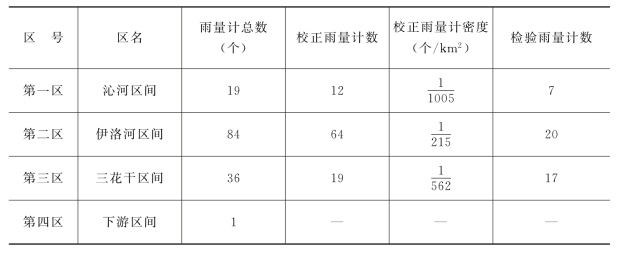
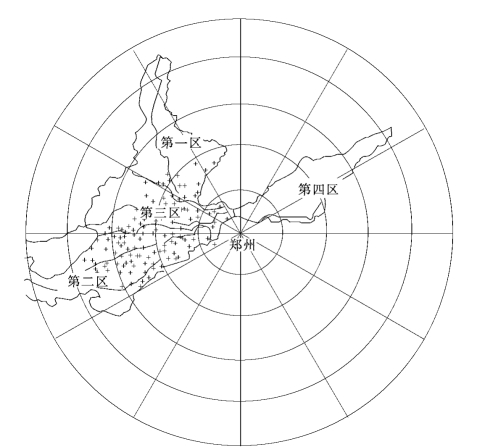
图11-13　黄河流域集水区和遥测雨量计位置

2.实验结果

2000年汛期,郑州雷达采集到大量(10min一个周期)的体积扫描资料,6～8月期间几次暴雨过程的采样大小见表11-3。

表11-32000　年6～8月暴雨过程采样

这里选择2000年8月17日21时至18日16时的暴雨过程为例,说明雷达定量估测降水经雨量计校正后误差的大小,其他暴雨过程计算的情况类同。

表11-4～表119分别为用改进的卡尔曼滤波计校正后得到的1h、2h和3h雨量计和雷达测量集水区面累积平均降雨量的大小,以及雷达降雨和雨量计相比较的相对误差,表中Rg 为雨量计数值,Rr 为校正后的雷达估测值。图11-14～图11-20 分别为用改进的卡尔曼滤波方法校正后的1h、2h、3h、6h的累积降雨量图。

表11-4　2000年8月18日3时～9时雷达估测集水区每1h累积平均降水量的相对误差

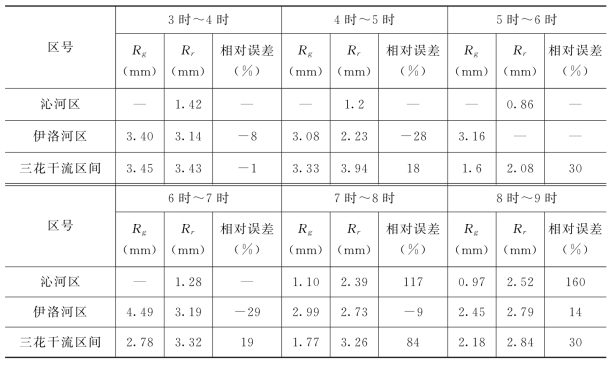
表11-5　2000年8月18日3时～5时雷达估测集水区每2h累积平均降水量的相对误差

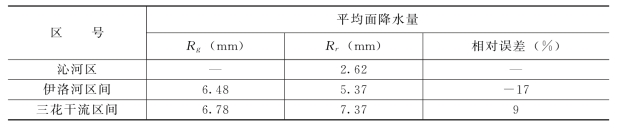
表11-6　2000年8月18日7时～9时雷达估测集水区每2h累积平均降水量的相对误差

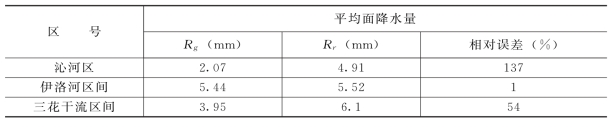
表11-7　2000年8月18日3时～6时雷达估测集水区每3h累积平均降水量相对误差

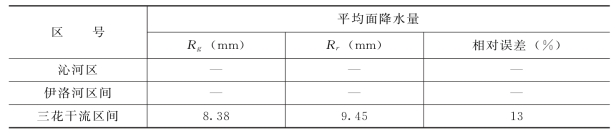
表11-8　2000年8月18日6时～9时雷达估测集水区每3h累积平均降水量的相对误差

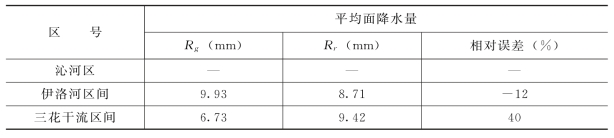
表11-9　2000年8月18日3时～9时雷达估测集水区每6h累积平均降水量的相对误差

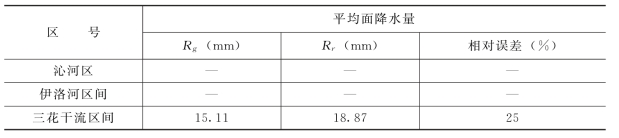
图11-14　2000年8月18日3时～4时1h累积降水量

图11-15　2000年8月18日4时～5时1h累积降水量

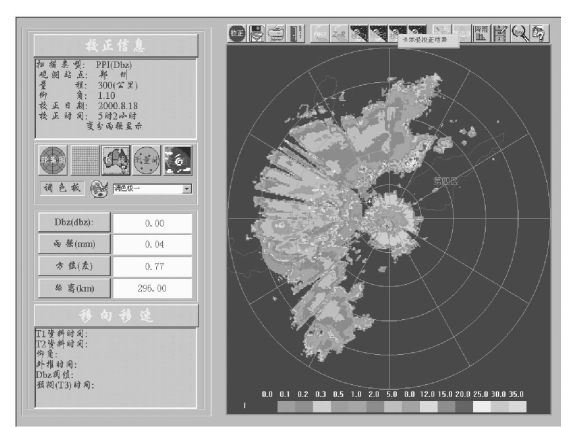
图11-16　2000年8月18日3时～5时2h累积降水量

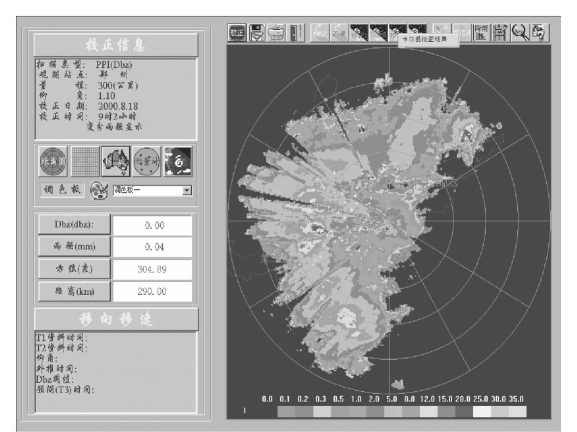
图11-17　2000年8月18日7时～9时2h累积降水量

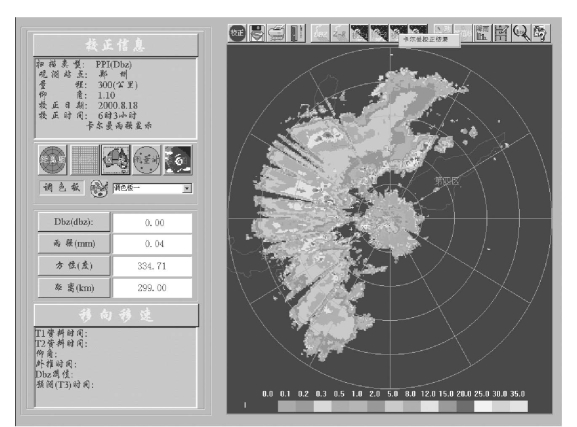
图11-18　2000年8月18日3时～6时3h 累积降水量

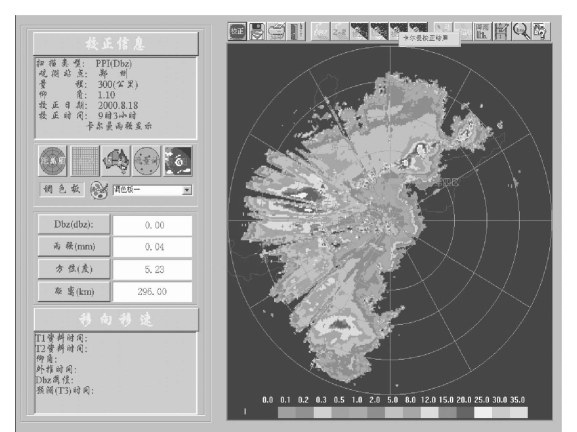
图11-19　2000年8月18日6时～9时3h累积降水量

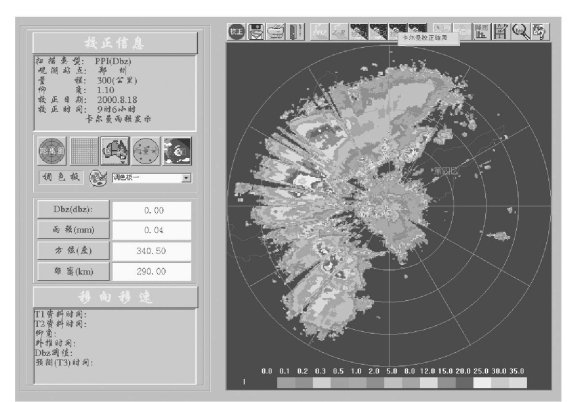
图11-20　2000年8月18日3时～9时6h累积降水量

雨量计平均面降雨量的计算(算术平均):

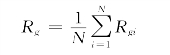
式中:Rgi为集水区中第i 个雨量计(这里的雨量计是指检验雨量计)的累积降雨量。

雷达估测平均面降雨量的计算

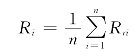
式中:Rri为集水区第i个像素点上雷达估测的累积降雨量。

从上面的列表计算结果中可以看出,用研究的新算法定量测量降水系统,在实际工作中能够有效的提高雷达测雨精度。对于1h、2h、3h和6h的降水,雷达测量降水量的精度都有较大幅度的提高。雨量计记录比较多,降雨比较集中的三花干流、伊洛河区间,校正后雷达估测的3h面累积降雨量的相对误差为13%、12%、40%,平均相对误差为22%。1h的雷达估测累积降水量的误差一般小于30%(当然当雨量计观测误差比较大,雨量记录比较少时,1h的误差可能大于100,如三花干流区7时～8时雷达估测的1h面降雨量),2h的误差一般小于20%,个别情况下(雨量记录比较少时)大于50%,而6h的累积面降雨量的误差小于25%。当雨量记录比较少时(有时只有一个或几个雨量计记录到降雨量),雷达估测的相对误差可达到面累积的50%以上,如沁河区。

以上说明当面累积降雨量大于5mm 时,雷达估测面降雨量的相对误差小于20%。此外,不难看出雷达估测面降雨量的精度随累积时间的增加而提高,即6h的累积面降雨量估测精度最高,1h的估测精度最低。

在这里,我们没有计算12h和24h的雷达估测面降雨量,主要原因是资料缺乏,在实验区内的连续降水不到24h并且有效配对的资料(即雨量计资料和雷达资料匹配)不到12h,另外2000年大多数降水不是在我们的研究区内,因此没有相应的雨量计资料。此外,由于资料的缺乏,样本不够,我们无法通过窗概率配对的方法获得校准区的Z—I 关系,我们用到的关系是经典的层状云Z—I关系:Z=200I1.6。

五、存在的问题及展望

1.存在的问题

在本次实验中,2000年大多数强降水不是在我们的研究区内,因此没有相应的雨量计资料,即使在实验区中的降水持续时间也不到24h,并且有效配对的资料(即雨量计资料和雷达资料匹配)不到12h,因此无法计算出12h和24h的雷达估测面降雨量。此外,由于资料的缺乏,样本不够,我们无法通过窗概率配对的方法获得校准区的Z—I 关系,希望今后能收集到足够的资料进行计算。另外,在2000年的实验中,由于某些时次雨量计和雷达观测的误差以及雷达雨量计的不匹配,给实际计算带来了很大的误差。比如两个站相距不超过10km,一个站1h降水量高达30mm,而另一个站仅为0.1mm,从雷达回波图上看来两个站位于同一降水区内,而且相差不应该超过1mm。另外,雷达回波接收质量不太好,一是受到较多的阻挡,另外就是发生遗失径向数据的问题,从而造成回波不连续,也容易造成雷达雨量计观测的不匹配,希望在以后的观测中尽量提高观测质量,减少这种误差。还有一个问题是雷达生产厂家提供的资料是原始的dB数码资料不是dBz资料,而雷达生产厂家并没有给出雷达标定后的参数以及其dB转化成dBz的公式,因此我们的系统在实际应用中采用的计算是根据其出厂的714CD 统一的参数计算得来的,这也可能在校正过程中产生误差。最后一个问题是,目前我们改进的卡尔曼滤波法考虑了测量过程中的噪声是高斯白噪声,在以后的工作中将考虑滤除有色噪声的情况,对算法做进一步的改进。

2.展望

在雷达估测降雨量中,雷达反射因子Z—R 之间的关系已经应用了几十年,虽然反射因子的高值与高的降雨强度相对应,但是这两者之间不存在唯一的关系。降雨强度和雨滴大小分布有关系,通常雨滴大小的分布可以用一个多参数的函数来描述,而在Z—R 关系中常常把雨滴大小的分布定为一个单参数。当然雨滴谱的变化只是影响雷达测雨精度的许多因子中的一个,而且未必是最重要的影响因子。

在雷达测雨中,双线偏振多普勒雷达具有其优越的性能,它改进了对降水类型的识别和提高了定量测雨的精度。大多数天气雷达在增加偏振性能时都要采用双线偏振波,雷达交替地发射水平偏振和垂直偏振脉冲,从而可以得到水平偏振的雷达反射因子ZH 和垂直偏振因子ZV。在增加一个可以接收S发射偏振波相垂直的偏振波接收机以后,就可以接收正交的偏振信号ZVH,即发射垂直偏振波,接收返回信号的水平偏振分量。对于多普勒雷达还可以估测水平和垂直偏振波返回的相位差:ΦDP=ΦV-ΦH,ΦDP 也称为差分传播相位差,它还可以用另一种形式即比差分传播相位移KDP 来表示。KDP 近似的为ΔΦDP/2Δr,这里ΦDP 是差分传播相位差在Δr的径向距离上的变化率,它是一种向前传播效应,和雨强R 成比例。已经证明KDP 对雨滴大小分布不敏感,而且克服了其他许多限制测量精度的因素,如雷达的标校误差；由于湿天线罩和电磁波传播路径中的雨的衰减；部分波束的截断；确定雨和冰雹分界的反射因子阈值的偏差,这种偏差引起对极端降雨量估计过低；以及地杂波对消的偏差等,从而提高了估测降雨量的精度。