近些年来,数值模式有了长足的进展。1997～1999年黄委应用中国科学院大气物理研究所宇如聪博士开发的η坐标模式(LASGREM),表明该模式作为黄河中游数值预报模式,其基本框架是合理的,对黄河中游的气候特点模拟较好,考虑了变地形的影响、行星边界层(PBL)和整个自由大气之间的相互作用过程等,如低层的地面风、地面对太阳辐射的吸收放射、地面温度、湿度及其通量等微物理过程,中、高、低云系的性质及其对大气过程的影响,大尺度、小尺度降水的湿对流过程,以及能量和对流的调整等。为了适应黄河防洪的需要,在低分辨率的模式(75km,REM)基础上,改进为高分辨率(34km,AREM)模式。

一、数值模式的简况及AREM 的特点

暴雨是影响我国的主要灾害性天气,暴雨引起的洪涝灾害常给我国国民经济建设和人民生命财产带来巨大损失。据有关部门统计,近几年,我国因暴雨洪涝灾害所造成的经济损失年平均已达上千亿元,约占国民生产总值的3%～6%。1991 年经济损失为1215 亿元。1994 年损失高达1876 亿元。1995年6～7月,两个月损失超过600亿元。1998年则发生了1954年以来最大的洪涝灾害。因此,暴雨的研究和预报受到各部门的广泛关注,它是预防洪涝灾害的极为重要的问题。暴雨的发生有很强的局地性,其一个显著的特征是与地形有密切的关系,暴雨预报也是国际上公认的难题。黄河流域处于东亚季风区,地域辽阔,地势西高东低,形成三级阶梯地形,降水中心受地形影响很大,如秦岭、太行山、吕梁山等对降雨的形成起明显作用,独特的地形地貌和多变的气候环境,增加了暴雨数值预报的复杂性和困难性,暴雨数值预报也是预报黄河暴雨的关键技术。

地形对天气和气候的影响是很复杂的。在大气数值模式中,如何恰当地描述地形作用,一直是国际上的研究难点。目前许多的大气数值预报模式在考虑地形方面都是采用一种气象上称为σ坐标的垂直坐标系。σ坐标的表达式为:σ=(p-pt)/(ps-pt)。对于这种坐标系,等σ面是随地形起伏而起伏,在大气底部,等σ面与地形下垫面重合,这样,在数值模式中,可给出一个简单下边界条件。但是,当地形比较复杂时,这种坐标模式也存在着一些问题。归结起来,其主要问题有:

(1)当地形比较陡峭时,σ等坐标面将非常倾斜。沿着这样的σ面,计算气压梯度力的误差比较大,从而,模式不能合理地反映出山脉对气流的阻挡作用。

(2)实际,大气具有准水平的层流特性,以陡峭的σ面作为分层气流数值模式的平面不太合理。

(3)沿陡峭的σ面,计算物质平流和水平扩散等误差都较大。

以上问题,在陡坡地形上空尤为严重,这就使得σ坐标模式在考虑地形时只好取比实际地形平缓、光滑的格点平均地形,但地形作用是与它的坡度和形状密切相关的,如何解决这些问题,一直是国际上广泛讨论的难点。为此,国内外许多科学家想了不少办法,如曾庆存先生1963年提出的标准层结静力扣除法,在国际上现已很著名,并被一些先进国家采用。为解决σ坐标面倾斜的问题,曾先生在1982 年曾提出过一种修正的σ 坐标,与Mesinger在1984年发表η坐标基本一致。η坐标的表达式为:η=σ×ηs,其中,ηs= [pref(Zs)-pt]/[pref(Zb)-pt]。η坐标保留了σ 坐标的优点,下边界条件简单,而克服了σ坐标的缺点,使坐标面为准水平。

中国科学院大气物理研究所(IAP)大气科学和地球流体力学数值模拟国家重点实验室(LASG)自1986年以来设计建立了一个能考虑我国复杂地形的η坐标的有限区域数值预报模式。针对暴雨模式中水汽平流处理的困难,该模式设计了适合我国计算机能力的有很好计算效果的保形正定输送方案,以适合暴雨模式中具有强梯度分布特征的水汽传输,保证了模式中与暴雨直接关联的水汽计算的精度。为了使研究工作不仅仅停留在数值试验和理论研究上,LASG 和有关单位一起为该模式的实际应用和业务化做了大量富有成效的工作。为进行实时预报试验,该模式建立了包括解码、检误、质量控制和客观分析为一体的初始处理系统。

AREM 的特色主要包括:

(1)该模式的动力框架采用了曾庆存先生设计的唯一能构造出完全能量守恒时空差分格式的数学模型,模式具有很好的计算稳定性。

(2)对复杂地形,采用了目前国际上最先进的计算方法和处理技巧,有效地解决了复杂地形所带来的计算问题,使得模式能较好地考虑真实地形的作用(如采用η坐标、静力扣除、协调性等技术应用)。

(3)对水汽平流方程设计了一个适合我国计算机条件的简单而有效的保形正定平流差分方案,并解决了在E 网格中的应用问题,避免了大多数模式中常出现的负水汽现象或平滑耗散过强现象,保证了模式对降水范围、降水强度和暴雨中心位置有更好的预报。

(4)保留了初始场的静力平衡偏差,在静力平衡模式中,同时保留了位势高度和温度场的初值意义,而目前许多静力平衡模式基本上是只考虑位势高度和温度场之一的初值意义。

(5)变量在网格上的分布形式采用了较合理的交错分布方法,并对重力波解在网格上的分离,设计了有效的计算方法。

(6)模式考虑了影响短期天气演变的主要物理过程,设计思想以简单有效为宗旨。主要包括:网格尺度的凝结降水、Betts的积云对流调整方案、整体边界层参数化。

(7)程序结构为分解式,便于吸收新的物理方案。显式分解的时间积分方案,提高了计算速度。

(8)模式范围、位置、分辨率和积分时间等的改变较灵活。

(9)可适合各种计算平台,计算速度快,对硬件的要求低,适应性强。

二、模式的基本方程组

1.p 坐标下的原始方程组

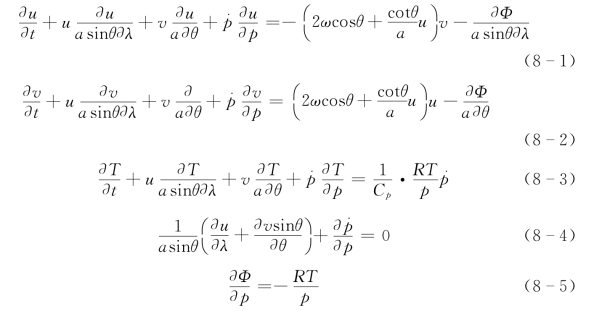
式中:λ和θ 分别为经度和余纬；p 为气压；t为时间坐标；u、v、T 和Φ分别为纬向风分量、经向风分量、大气温度和位势高度；a 和ω 分别为地球半径和地球旋转角速度；R 和Cp 分别为干空气的气体常数和定压比热。

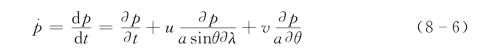
2.相对于标准层结的扰动方程组

引进满足如下条件的标准层结大气:

由式(8-10)可得:

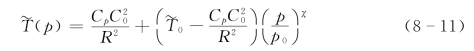
把式(8-11)代入式(8-9)可得:

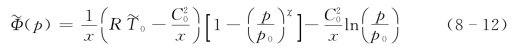
对式(8-12)取p=ps 又得到:

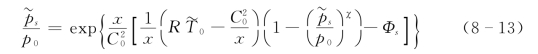
式中:χ=R/Cp；p0 和T0 分别为标准海平面气压和标准海平面气温；C0 为定常重力波速。由式(8-11),我们要求参数p0、T0 和C20 满足:

式(8-11)、式(8-12)、式(8-13)就是标准层结大气的温度,位势和地面气压的表达式。

实际大气的温度和位势可表示为

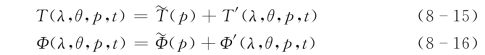
把式(8-15)和式(8-16)代入式(8-1)～式(8-5),整理后得到扰动方程组:

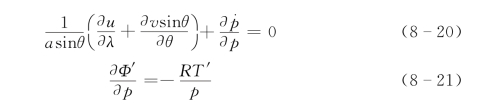
其中,T′和Φ′是相对于标准层结的扰动温度和位势。在得到式(8-19)时用到了如下的推导:

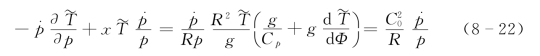
3.η坐标下的扰动方程组

对方程式(8-17)～式(8-21)作η坐标变换:

式中:zs 是模式中的地形高度；zb 是用来构造坐标面的平缓地形；prf(z)是标准层结大气在z高度处的气压；pt 和ps 分别表示模式顶气压和地面气压。

其导数关系为:

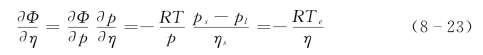
其中

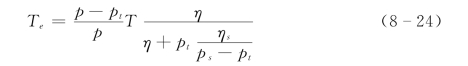
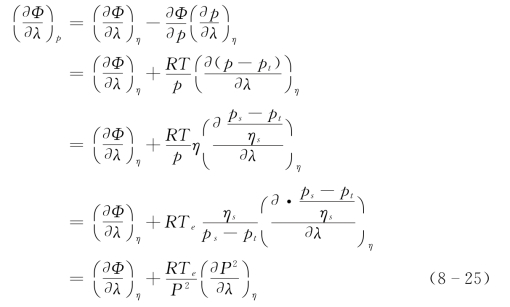
其中

同理

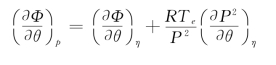
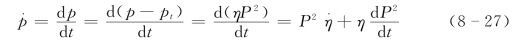
其中

对式(8-17)～式(8-21),利用式(8-23)～式(8-33)可得η坐标下的扰动方程组:

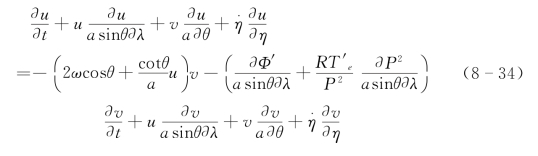
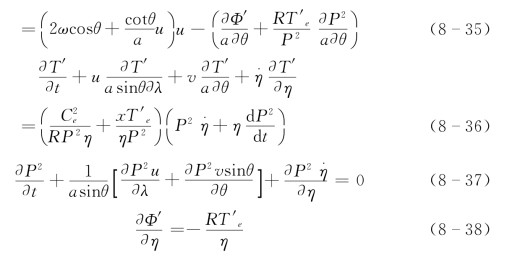
其中

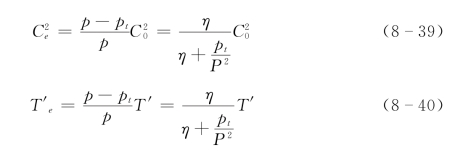
构造差分模式的方程组形式:

对方程式(8-34)～式(8-38)作因变量变换:

并略去扰动位势和温度的上角标′。

设F=Pf,f 表示任一因变量,则存在下列关系式

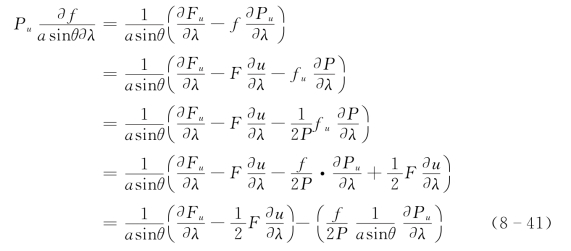(www.daowen.com)

同理

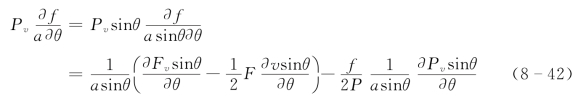
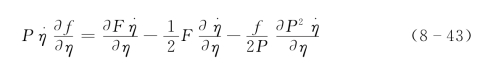
另外

由式(8-37)

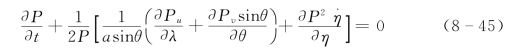
利用边界条件对式(8-45)作0→ηs 积分得

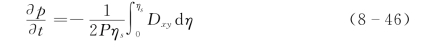
作0→η积分得

利用式(8-41)～式(8-47)整理因变量后可以得到本模式干动力框架的基本方程组:

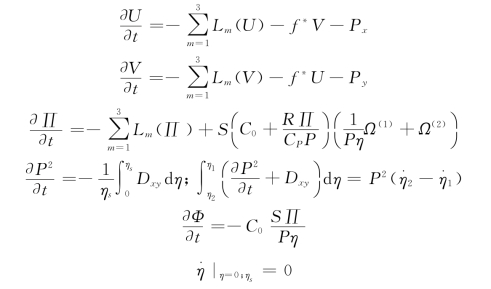
其中

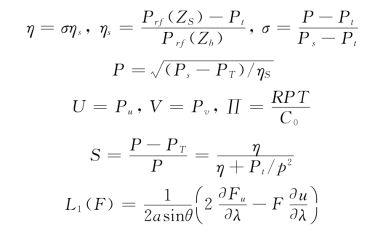
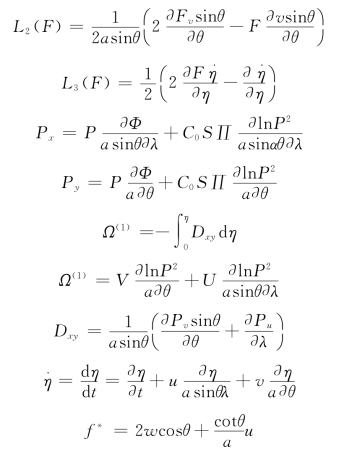
三、网格分布和地形

1.变量在水平网格上的分布形式

变量在水平网格上的分布形式如图8-2所示。

2.变量在垂直方向上的分布形式

变量在垂直方向上的分布形式如图8-3所示。

四、空间差分格式

在以下差分方案中,为讨论方便,将高度场格点和速度场格点混在一起排序,第一格点(1,1),为高度格点,沿纬向方向,第二格点为(3/2,1),沿经向第二格点为(1,3/2),差分计算的格点序号(i,j,k)包括i=1,3/2,…,I+1/2；j=1,3/2,…,J-1；k=1,2,…,K；其中,满足i+j=LL+1/2(LL 为整数)的点为速度场格点,满足i+j=LL 的点为高度场格点。

1.水平平流差分格式

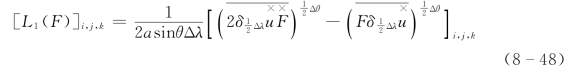
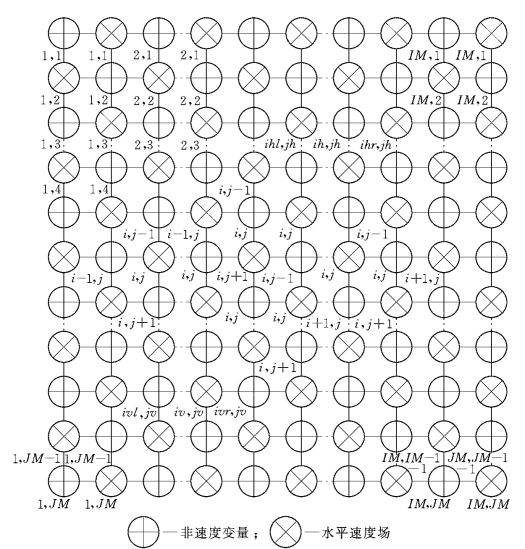
图8-2　变量在水平网格上的分布形式

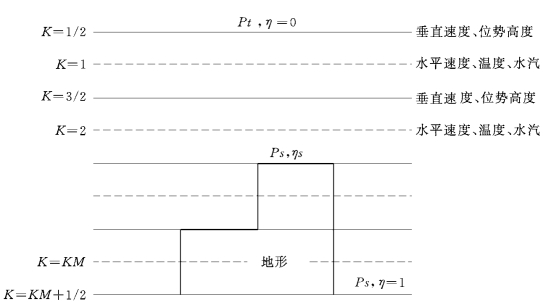
图8-3　变量在垂直方向上的分布形式

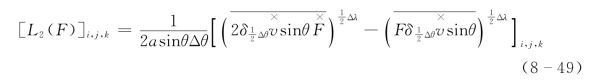
整理后得

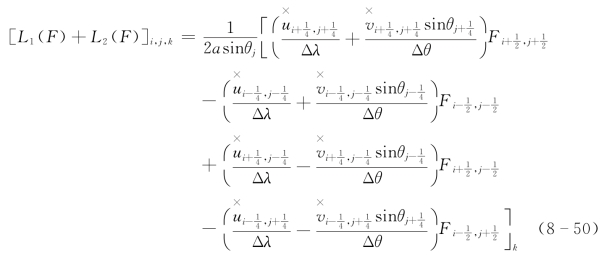
若F 表示U 或V 则

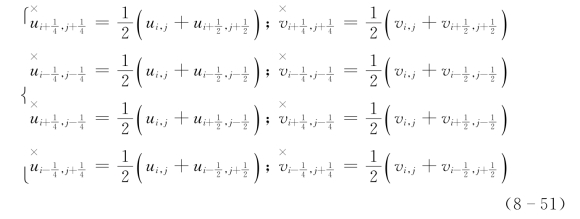
若F 表示∏,则

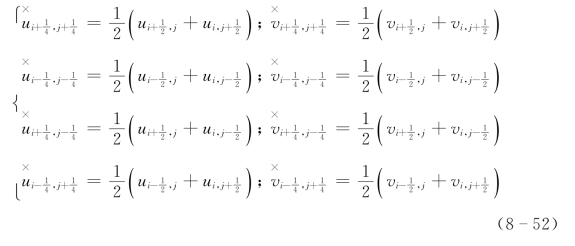
2.垂直平流差分格式

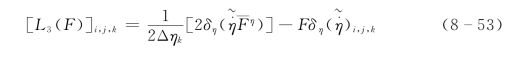
若F 表示U 或V,则若F 表示∏,则其中

3.动能、位能相互转换项的差分

4.质量散度差分格式

E 网格可以理解为两个C 网格对角平移一半对角线的叠加,当纯重力波方程在E 网格变量分布下采用空间中央差分时,这两个子C 网格的解相互独立,从而产生虚假的二位格距波。在本模式中,我们用半格距沿网格线的气压梯度力散度和常规整格距计算的气压梯度力散度之差修正水平质量散度差分解决了这一问题。用下角标“+”和“×”分别表示按正常的整格距差分计算和按半格距差分计算。修正后的水平质量散度差分方案为

其中

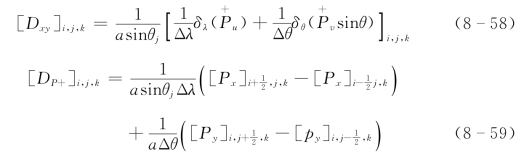
式中的[Px]i,j,k 和[Py]i,j,k 见式(8-55)。

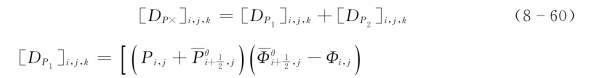
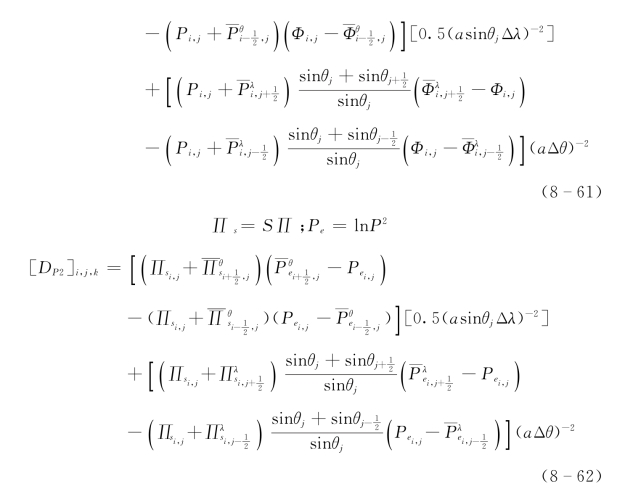
5.诊断量的计算

(1)η.的计算。结合式(8-5)可得

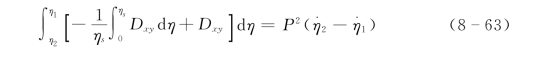
由式(8-63)和式(8-7)得η.的计算格式:

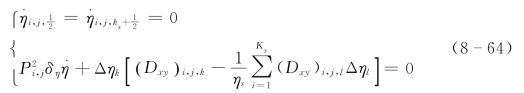
(2)Φ 的计算。考虑到应充分保留初始场信息,保持起始积分与中间积分的一致性,位势高度Φ 的计算格式设计如下。

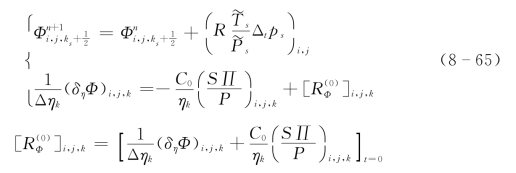
式中: 分别为标准层结大气的地面温度和地面气压；上角标n 为积分的时步；为初始场的差分静力平衡误差。

6.扩散项的差分格式

为了使水平扩散须差分格式涉及到所有周围邻点的不均匀性,类似于前一章中对平流差分格式和质量水平辐合辐散修正差分格式的处理,我们用整格距水平扩散差分和半格距水平扩散差分的加权平均来构造水平扩散的差分格式。

记Δ′F= ∇·(G∇F),下面给出计算Δ′F 的整格距和半格距差分格式Δ′+F 和Δ′×F:

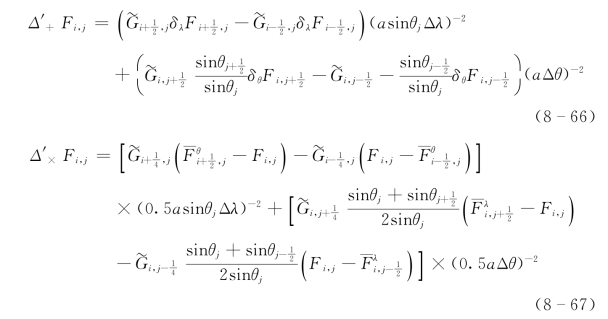
其中,如果F 代表T 或q,则G 在格点上的分布与F 重合,且

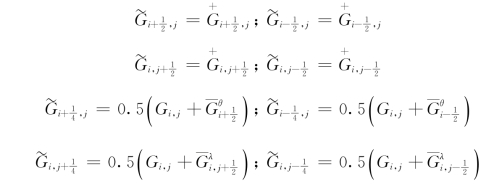
如果F 代表u 或v,则G 在格点上的分布与F 交错,且

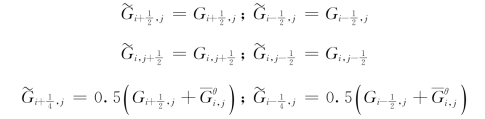
垂直扩散的空间差分格式取中央差。

可以证明,当不考虑源汇项时,上述空间差分格式在一定的边界条件下和时间差分方案下,保留了原微分方程组的下列性质:总质量守恒；非线性平流不破坏能量守恒；科里奥利(Coriolis)力单点不做功:由η 坐标面倾斜所出现的气压梯度力修正项产生的动能与绝热修正项产生的位能相抵消(在原微分方程是单点性质,而这里是整体性质)；总有效能量守恒。