物体在转动时，它的各点都在做圆周运动。物体在做圆周运动时出现向心力和离心力两个力。

1.向心力

如图3-27（a）所示的实验，用绳的一端系一小球，绳的另一端用手拉住，使小球做圆周运动，转动半径为R，小球的线速度为v。小球在做圆周运动时受到绳子的拉力F的作用，这个力的方向总是沿着绳子指向圆心，因此力F称为向心力，它与线速度方向垂直。

在圆周运动中，物体线速度的方向不断地改变，就是由于向心力的作用。如果绳子突然断开，如图3-27（b）所示，小球就会失去向心力，那么小球就会由于惯性而沿切线方向飞去。

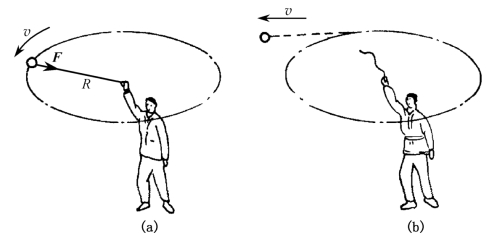
图3-27　使小球做圆周运动

实践证明，物体做圆周运动时，向心力F的大小与线速度v的大小、圆的半径R的大小以及物体的质量m有关，它们的关系可由式（3-31）表示。

2.离心力

当手拉着绳子使小球做圆周运动时，我们会感到小球对绳子也有一个拉力的作用，方向离开圆心，这是向心力的反作用力，叫作离心力。根据作用和反作用定律可知，离心力和向心力总是成对地出现，大小相等、方向相反，分别作用在两个物体上。向心力作用在做圆周运动的物体（小球）上，离心力作用在施力物体（绳子）上，所以物体（小球）在做圆周运动时，具有沿着切线方向离开圆心的趋势，在生产实际中，有些机器和机构是利用这一原理制成的。例如：离心水泵、离心油水分离器以及发动机上常用的离心调速器等。而有些机器和机构却由于离心力作用而产生振动、零件磨损以及影响工作质量等严重的不良后果。

3.力矩、功率和转速三者关系(www.daowen.com)

图3-28表示一轮子在A点受到与半径R相垂直的力F以后，以转速n绕轴心O转动，A点的线速度为v。在这种情况下，功率P可按P＝Fv公式来计算。因为前面式（3-31）可知，，所以

式中　FR——力F对O点的力矩，称为转矩，以MO表示，因此式（3-33）可写成

经换算，有

式中，转矩MO的单位是N·m，转速n的单位是r／min，功率P的单位是kW。

从式（3-34）中可以看出，物体在转动时，转矩MO与功率P成正比而与转速n成反比。机床上电动机的额定功率都是一定的，因此转速越高则转矩越小。如果用割刀切断工件，则这时需要有大的转矩，必须降低转速。汽车爬坡时，需要降低车轮的转速来增大转矩，以适应爬坡的能力。

图3-28　轮子转动情况