上面讨论了两个相对接触的物体在做相对滑动趋势时的滑动摩擦问题。现在来讨论工程实际中常常遇到的另一类摩擦问题，即滚动摩擦问题。

图3-24（a）表示一放在水平面上的滚子，它的质量为Q，半径为r，在滚子中心处作用着一水平力F。由实践可知，当作用力F不太大时，滚子仍能保持静止状态。这时在滚子上除了受到水平力F和重力Q以外，还受到水平面的法向反力FN和静摩擦力F′的作用。我们知道，滚子在力F的作用下，一方面有沿力F方向滑动的趋势，同时也有绕接触点滚动的趋势。摩擦力F′阻止了滚子的滑动，但它不能阻止滚子的滚动。那么，究竟是什么力阻止了滚子的滚动呢？因为滚子压紧在水平面上，接触面处会发生一定的变形，如图3-24（b）所示，此时反力FN的作用线实际上已经向前移动了一段距离δ。力F和F′组成一力偶，它使滚子滚动；而重力Q和FN组成的另一力偶力图阻止滚子的滚动。这种力偶称为滚动摩擦力偶。

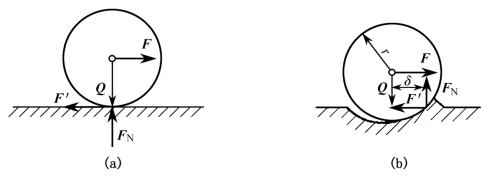
图3-24　滚动受力分析

当力F在一定范围内逐渐增大时，力FN移动的距离δ也随之相应地增大，滚子还能保持静止状态。当力F增大到某一临界值时，滚子处于将要滚动而尚未滚动的临界状态，距离δ增大到最大值。这时使滚子产生滚动的力偶的力偶矩为Fr，滚动摩擦力偶的力偶矩达到最大值，即

式中　δ——法向反力FN移动的最大距离，它具有长度的量纲，称为滚动摩擦系数，其大小与接触物体的材料和接触面的情况有关，而与滚子半径的大小无关，其数值可查有关手册。(www.daowen.com)

根据上面分析可知，使滚子产生滚动的条件是

由此可知，使滚子产生滚动所需的力为

而使滚子产生滑动所需的力为

由于δ／r远小于动摩擦因数f′，因而F′≫Fr，这就是滚动比滑动省力的原因。