1.力坐标的建立

设在物体的某点O作用一力F，并选取坐标轴x与y，如图3-14所示。自力F的两端分别向x、y轴作垂线。Oa称力F在 x轴上的投影，记为FX；Ob称力F在 y轴上的投影，记为FY。

图3-14　力在坐标上的投影

（a）与坐标轴同向；（b）与坐标轴反向

2.力投影的方向

一般规定力的起端到末端的投影方向与坐标轴的正向相同时，投影为正，反之为负。如图3-14（a）、（b）所示。

3.力在坐标轴上的投影的代数量

当力与坐标轴垂直时，力在该轴上的投影为零；当力与坐标轴平行时，力的投影的绝对值等于力本身的大小。

4.合力投影定理

指合力在某一轴上的投影，等于力系中各力在同一轴上的投影的代数和。

例3-4　在三脚架ABC的销B上悬挂一重G＝1000N的物体，如不计杆AB、BC的自重，已知α＝45°，β＝30°，试求杆AB和BC所受的力。

解：为了求出三脚架中杆AB和BC所受的力，可取销B为研究对象。销B受到三个汇交力的作用，如图3-15所示。

（1）已知力G；

图3-15　销B点受力分析(www.daowen.com)

（2）杆AB和BC为二力杆，其反力F1和F2沿着杆的轴线，杆AB受拉，杆BC受压。

取直角坐标系：由平面汇交力系的平衡方程得

根据作用与反作用定律，杆AB和BC所受的力为：杆AB受拉力F1＝513N，杆BC受压力F2＝732N。

例3-5　物体重力 Q＝2×104N，利用绞车和绕过定滑轮B的绳子吊起物体，如图3-16（a）。滑轮由两端铰链的钢杆AB和BC支持，杆和滑轮的重量均可不计。试求钢杆AB和BC所受的力。

图3-16　滑轮B点受力分析

解：（1）求钢杆AB和BC所受的力，取B为研究对象。

（2）滑轮的受力分析：如图3-16（b）所示，滑轮受两边绳子的拉力F和物体重力Q的作用，因不计滑轮的摩擦，F＝Q＝2×104N，杆AB和BC的反力F1和F2的方向都是沿该杆两端铰链中心的连线，假定这两个力都是压力，即假定两杆本身都受压。

（3）取坐标轴，写出滑轮的平衡方程并求解。

所以

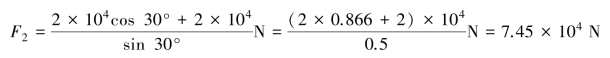
所以

F1＝2×104sin30°-F2cos30°＝-5.45×104N

F1为负值，这表示力F1的实际指向与假定的指向相反，即杆AB实际上受拉力。