公差带是由公差带大小和公差带位置两部分构成的，大小由标准公差决定，而位置则由基本偏差确定。为满足机器中各种不同性质和不同松紧程度的配合，需要有一系列不同的公差带位置以组成各种不同的配合。

1.孔、轴的基本偏差及其代号

基本偏差是指两个极限偏差中靠近零线或位于零线的那个偏差。因此公差带在零线之上的，以下极限偏差为基本偏差；公差带在零线之下的，以上极限偏差为基本偏差。如图2-15所示，孔的基本偏差为下极限偏差（EI），轴的基本偏差为上极限偏差（es）。

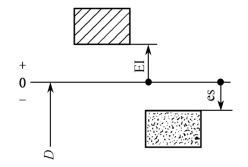
图2-15　基本偏差

为了满足各种不同配合的需要，国家标准对孔和轴分别规定了28种基本偏差，用拉丁字母表示，大写字母表示孔，小写字母表示轴。26个字母中除去5个容易与其他含义混淆的字母（孔去掉 I，L，O，Q，W，轴去掉 i，l，o，q，w），剩下的21个字母加上7个双写的字母（孔加上CD，EF，FG，JS，ZA，ZB，ZC；轴加上 cd，ef，fg，js，za，zb，zc），共 28种，作为基本偏差的代号。这28种基本偏差构成基本偏差系列，如图2-16所示。

从图2-16中可以看出：基本偏差系列中的H（h）其基本偏差为零。

JS（js）与零线对称，上极限偏差 ES（es）＝+IT／2，下极限偏差 EI（ei）＝-IT／2，上、下极限偏差均可作为基本偏差。

在孔的基本偏差系列中，A～H的基本偏差为下极限偏差EI；J～ZC的基本偏差为上极限偏差ES。

在轴的基本偏差系列中，a～h的基本偏差为上极限偏差es，j～zc的基本偏差为下极限偏差ei。

2.基准制

在机械产品中，有各种不同的配合要求，这就需要通过各种不同的孔、轴公差带来实现。为了设计和制造上的经济性，把其中孔公差带位置（或轴公差带位置）固定，而改变轴公差带位置（或孔公差带位置），来实现所需要的各种配合，这种制度称为基准制。其中，前者称为基孔制，后者称为基轴制。

图2-16　孔和轴的基本偏差系列

（1）基孔制：基本偏差为一定的孔的公差带，与不同基本偏差的轴的公差带形成各种配合的一种制度，如图2-17（a）所示。

基孔制的孔称为基准孔，是配合中的基准件，它的公差带在零线的上方，且基本偏差（下极限偏差）为零，即EI＝0，上极限偏差为正值。以H作为基准孔的代号。

（2）基轴制：基本偏差为一定的轴的公差带，与不同基本偏差的孔的公差带形成各种配合的一种制度，如图2-17（b）所示。

基轴制的轴称为基准轴，是配合中的基准件，它的公差带在零线的下方，且基本偏差（上极限偏差）为零，即es＝0，下极限偏差为负值。以h作为基准轴的代号。

基准制确定后，基准孔（或轴）的公差带位置就相应确定，则可用非基准轴（或孔）公差带的不同位置来建立各种配合。

图2-17　基孔制与基轴制公差带

3.各种基本偏差所形成配合的特征

（1）间隙配合：a～h（或A～H）11种基本偏差与基准孔的基本偏差H（或基准轴的基本偏差h）形成间隙配合。其中a与H（或A与h）形成配合的间隙最大。此后，间隙依次减小，基本偏差h与H所形成配合的间隙最小，该配合的最小间隙为零。

（2）过渡配合：js、j、k、m、n（或 JS、J、K、M、N）五种基本偏差与基准孔的基本偏差 H（或基准轴的基本偏差h）形成过渡配合。其中js与H（或JS与h）形成的配合较松，获得间隙的概率较大。此后，配合依次变紧，n与H（或N与h）形成的配合较紧，获得过盈的概率较大。而标准公差等级很高的n与H（或N与h）形成的配合则为过盈配合。

（3）过盈配合：p～zc（或P～ZC）12种基本偏差与基准孔的基本偏差H（或基准轴的基本偏差h）形成过盈配合。其中p与H（或P与h）形成的配合过盈最小。此后，过盈依次增大，基本偏差zc与H（或ZC与h）所形成的配合过盈最大。

4.公差带代号和配合代号

把孔、轴基本偏差代号和公差等级代号组合，就组成它们的公差带代号。例如孔的公差带代号 H7、F5、M6、V5等，轴的公差带代号 h7、f5、m6、v5等。

把孔和轴公差带代号组合，就组成配合代号，用分数形式表示，分子代表孔，分母代表轴，例如 H7／f8、H7／m6、F5／h5、M7／h6等。

5.轴的基本偏差的确定

轴的各种基本偏差的数值应根据与基准孔H不同的配合要求来制定。轴的各种基本偏差的计算公式是经过实验和统计分析得到的，见表2-5。

表2-5　轴的基本偏差计算公式（D≤500mm）

利用轴的基本偏差计算公式，以尺寸分段的几何平均值代入这些公式求得数值后，再经尾数取整，就编制出轴的基本偏差数值表，见表2-6。

轴的基本偏差确定后，在已知公差等级的情况下，可以确定轴的另一个极限偏差。

当轴的基本偏差为上极限偏差es、标准公差为IT时，得出另一极限偏差（下极限偏差）为：ei＝es-IT。

当轴的基本偏差为下极限偏差ei、标准公差为IT时，另一极限偏差上极限偏差为：es＝ei+IT。

例2-4　利用标准公差数值表和轴的基本偏差数值表确定φ30f8的极限偏差。(www.daowen.com)

解：查表2-5得公称尺寸为30mm且基本偏差代号为f的轴的基本偏差为上极限偏差es＝-0.020mm，查表2-3得公称尺寸为30mm的IT8＝0.033mm，所以轴的另一极限偏差为下极限偏差：

ei＝es-IT＝-（0.020-0.033）mm＝-0.053mm

因此，轴的极限偏差分别为es＝-0.020mm，ei＝-0.053mm。

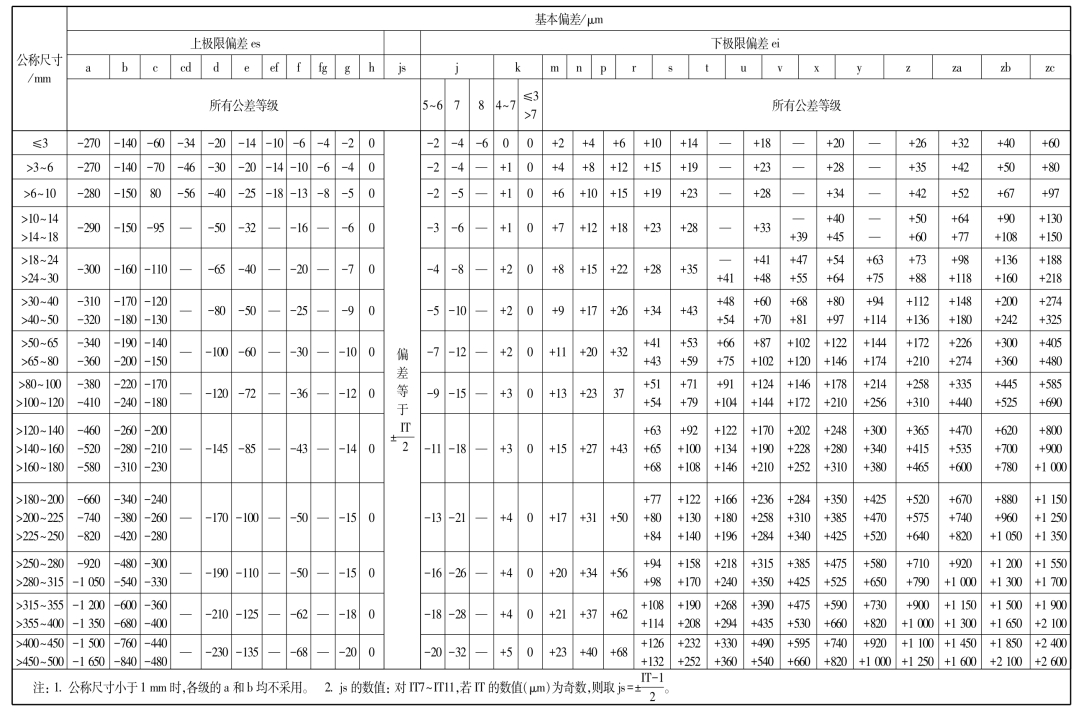
表2-6　尺寸≤500mm的轴的基本偏差数值

6.孔的基本偏差的确定

孔的基本偏差可以由同名的轴的基本偏差换算得到。换算原则为：同名配合，配合性质不变，即基孔制的配合（如φ70H8／f7）变成同名基轴制的配合（φ70F8／h7）时，其配合性质（极限间隙或极限过盈）不变。

根据上述原则，孔的基本偏差按以下两种规则换算：

（1）通用规则，参看图2-18，通用规则为用同一字母表示的孔和轴基本偏差的绝对值相等，而符号相反，即：EI＝-es或 ES＝-ei。

通用规则的应用范围如下：

从A到H［图2-18（a）］，不论孔和轴的公差等级是否相同，均采用通用规则，因为a到h的基本偏差为es，所以A到H的基本偏差为EI＝-es。

从K到ZC［图2-18（b）和图2-18（c）］，当孔和轴公差等级相同时，按通用规则换算，因为k到zc的基本偏差为ei，所以K到ZC的基本偏差为ES＝-ei。

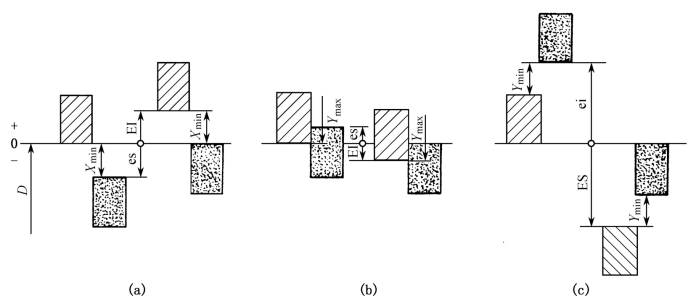
图2-18　通用规则

（a）间隙配合；（b）过渡配合；（c）过盈配合

（2）特殊规则：特殊规则为用同一字母表示的孔和轴基本偏差的符号相反，而它们的绝对值相差一个Δ值。

由图2-19可以看出：

基孔制中：　Ymin＝ES-ei＝ITn-ei

基轴制中：　Ymin＝ES-ei＝ES-［-ITn-1］＝ES+ITn-1

为了满足换算原则，基孔制的Ymin应等于基轴制的Ymin，因此

即

EI＝-es+Δ或ES＝-ei+Δ

Δ＝ITn-ITn-1

式中　ITn——孔的标准公差值；

ITn-1——轴的标准公差值。

图2-19　特殊规则

特殊规则的应用范围如下：

① J、K、M、N的公差等级为8级或高于8级（标准公差≤IT8）时，采用特殊规则；

②P～ZC的公差等级为7级或高于7级（标准公差≤IT7）时，采用特殊规则。

按上述两个规则，可计算并编制出孔的基本偏差数值表，见表2-7。

例2-5　利用标准公差数值表和轴的公称偏差数值表，按 φ45H7／s6确定 φ45s7／h6中孔的基本偏差数值。

解：查标准公差数值表2-3得公称尺寸为45mm的IT7＝0.025mm，IT6＝0.016mm；查表2-5得公称尺寸为45mm且基本偏差代号为s的轴的基本偏差为下极限偏差ei＝+0.043mm。

因S7应按特殊规则换算，S的基本偏差为上极限偏差ES＝-ei+Δ，Δ＝IT7-IT6＝（0.025-0.016）mm＝0.009mm，所以，孔的基本偏差为 ES＝（-0.043+0.009）mm＝-0.034mm。

例2-6　利用标准公差数值表和孔轴的基本偏差数值表，确定φ80H8／r8和φ80R8／h8的极限偏差数值。

解：查标准公差数值表2-3得公称尺寸为80mm的IT8＝0.046mm；查表2-5和表2-7得公称尺寸为80mm、基本偏差代号为r的轴的基本偏差为下极限偏差ei＝+0.043mm，基本偏差代号为R的孔的基本偏差为上极限偏差ES＝-0.043mm。所以，φ80r8轴的另一极限偏差为es＝ei+IT8＝（0.043+0.046）mm＝+0.089mm，φ80R8的另一极限偏差为 EI＝ES-IT8＝（-0.043-0.046）mm＝-0.089mm。在 φ80H8／r8配合中，基准孔的基本偏差 EI＝0，另一极限偏差ES＝+0.046mm，es＝+0.089mm，ei＝+0.043mm，即 φ80H8（）／r8（）。在φ80R8／h8配合中，基准轴的基本偏差 es＝0，另一极限偏差 ei＝-0.046mm，ES＝-0.043mm，EI＝-0.089mm，即 φ80R8（）／h8（）。