立体的表面交线分为两种：一种是平面截割形体而产生的交线，称为截交线，这个平面称为截平面；另一种是由两个基本体表面相交而产生的表面交线，称为相贯线。

求截交线与相贯线的实质，就是求出形体表面一系列共有点的集合。

（一）平面立体截交线

平面立体的表面是由若干平面图形围合而成的，因此截交线是一个封闭的平面折线。折线的顶点往往是棱线与截平面的交点，每条折线是棱面与截平面的交线，如图1-45所示。

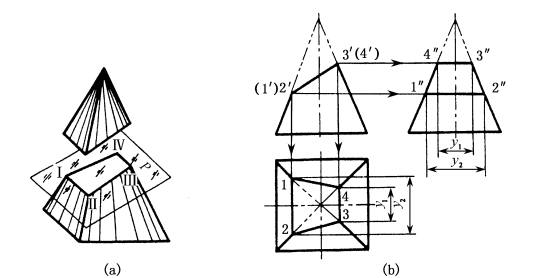
图1-45　切四棱锥

平面立体截交线的基本作图方法是：求出平面立体上参与相交的各棱线与截平面的交点，然后依次连接各点；也可直接求出平面立体上参与相交的各棱面与截平面的交线。

例1-1　如图1-45所示，求作斜切四棱锥的截交线。

作图步骤见图1-45（b）：

（1）因截平面的正面投影积聚成直线，故可直接求出截交线各点的正面投影（1′），2′，3′，（4′）；

（2）求出各顶点的 H面投影 1，2，3，4和 W面投影 1″，2″，3″，4″；

（3）依次连接各顶点的同面投影，即得截交线的投影；

（4）判别可见性，正确处理虚、实线。

例1-2　求作切槽四棱台的截交线。

分析：如图1-46所示，该槽由两个侧平面和一个水平面截割四棱台而成。两个侧平面在V面和H面上的投影都具有积聚性，水平面在V面和W面上具有积聚性。这样，该槽在V面上的投影具有积聚性。其侧面投影不可见，水平投影可见。

作图时，先画出四棱台三视图，然后作出切槽有积聚性的V面投影，然后再作出槽的W面投影，最后完成H面投影。

（二）圆柱的截割

因截平面与圆柱轴线的相对位置不同，圆柱的截交线有三种情况，见表1-10。

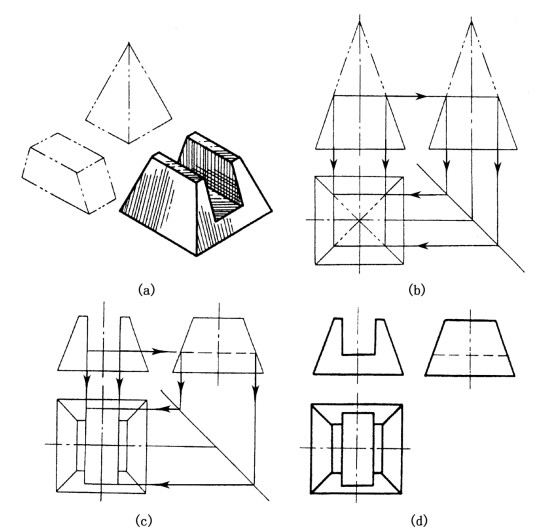
图1-46　切槽四棱台

表1-10　圆柱的截交线

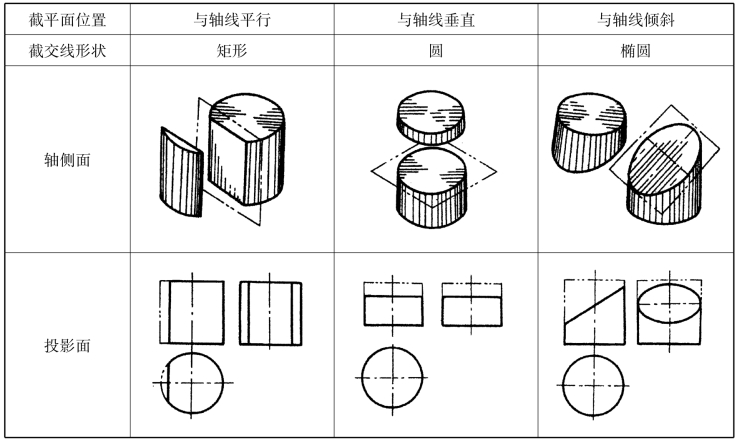
例1-3　作斜切圆柱的截交线。

分析：如图1-47所示，圆柱被正垂面所截，截交线为椭圆。椭圆在V面上的投影积聚为一条直线，在H面上的投影与圆柱面的具有积聚性的投影重合成一个圆，椭圆的W面投影仍为椭圆，根据点的投影关系即可作出，具体步骤如下：

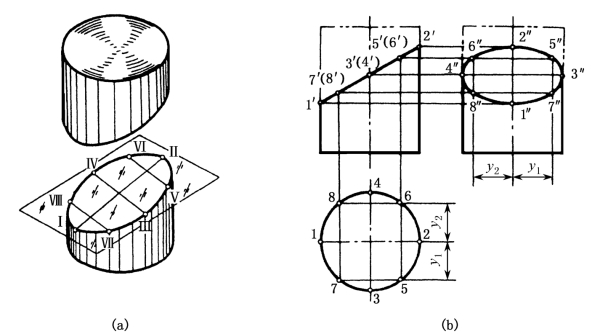
图1-47　斜切圆柱的截交线

（1）作截交线上特殊点的投影。特殊点指截交线上的最高、最低、最左、最右、最前、最后点，这些点往往位于圆柱的轮廓素线上。对于椭圆，须首先求出长、短轴的四个端点。长轴的端面Ⅰ、Ⅱ是椭圆的最高点和最低点（也是最左点和最右点），位于圆柱的最左和最右两条素线上。短轴的端点Ⅲ、Ⅳ是椭圆的最前和最后点，位于圆柱的最前和最后两条素线上。根据H面投影 1、2、3、4和 V面投影 1′、2′、3′、（4′）可求出侧面投影。

（2）作截交线上一般点的投影。在特殊点之间任取Ⅴ、Ⅵ、Ⅶ、Ⅷ各点，根据H面投影5、6、7、8和 V面投影 5′、（6′）、7′、（8′）可作出 W面投影 5″、6″、7″、8″。一般点选取的数量根据对作图准确程度的要求而定。

（3）依次光滑连接 1″、7″、3″、5″、2″、6″、4″、8″，即得截交线椭圆的 W面投影。

（三）圆球的截割

任何位置的截平面截圆球时，其截交线都是圆。当截平面平行于某一投影面时，截交线在该投影面上的投影为圆的实形，其他两投影面上的投影都积聚成直线，如图1-48所示。

例1-4　如画出螺钉头部的三视图。

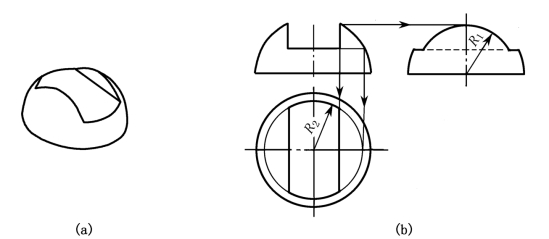
分析：如图1-49所示螺钉头部是一个中间开槽的半球体。它可以看成是用一个水平面和两个侧平面截割半球而成的形体。两个侧平面与半球的截交线各为一段平行于侧面的圆弧，其侧面投影反映实形。水平面与半球的截交线为两段平行于水平面的圆弧，其水平投影反映实形，具体步骤如下：

（1）画出半球的三视图。

（2）按槽深和槽宽画出截交线的V面投影。其在W面和H面上的投影，可按球面上平行于投影面的圆的画法作出。

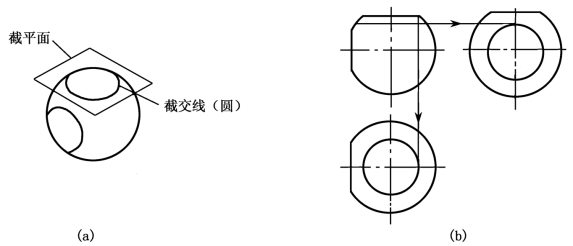
图1-48　圆球被投影面平行面所截切的三视图

(www.daowen.com)

图1-49　螺钉头部的画法

（3）判断可见性，正确处理虚、实线，完成全图。本例作图的关键是确定圆弧半径R1和R2，并判别槽底侧面投影的可见性。因半圆球上平行于侧面的圆球轮廓素线被切去一部分，所以由开槽而产生的轮廓线的侧面投影的半径R1小于半圆球半径R，同样R2也小于R，且槽底侧面的积聚性投影中有较长的一段不可见，故画成虚线。

（四）圆柱的相贯

圆柱的相贯线是相交两圆柱表面的共有线，一般为封闭的空间曲线。求其相贯线的投影可采用表面取点法和简化画法。

1.表面取点法（积聚性法）

如图1-50所示，当正交相贯两圆柱的轴线分别垂直于两个投影面时，两圆柱面在其轴线所垂直的投影面上的投影分别积聚成圆，由于相贯线是圆柱表面的线，故投影必重合在圆周上。作图时可利用已知点的两个投影求其他投影的方法画出相贯线上一系列点的投影，然后把所求的点顺序相连，即可得所求的相贯线，也即把求相贯线的问题变成了曲面上取点的问题。

例1-5　求两圆柱正交（轴线垂直相交）的相贯线。

分析：如图1-50所示，根据大、小圆柱轴线的位置，可以确定大圆柱面的W面投影和小圆柱面的H面投影都具有积聚性。因此，相贯线的H面投影与小圆柱面的H面投影重影，是一个圆；相贯线的W面投影与大圆柱面的W面投影重影，是一段圆弧。所以，只需求出相贯线的V面投影。具体步骤如下：

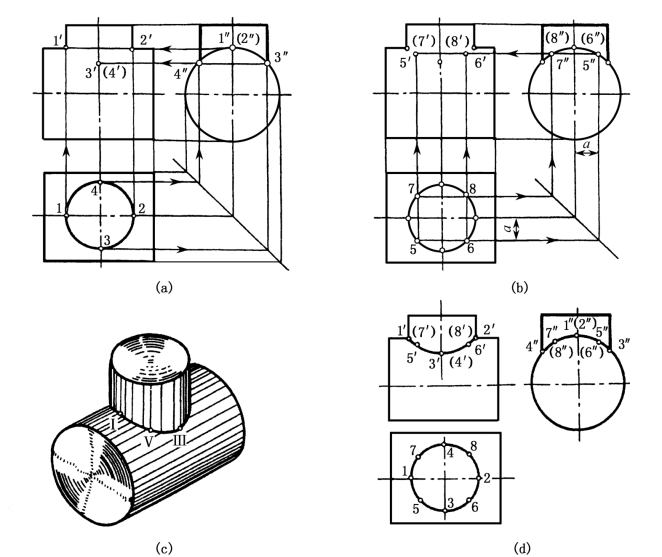
图1-50　两圆柱正交

（1）作相贯线上特殊点（轮廓线上的点）的投影。相贯线的最高点Ⅰ、Ⅱ（也是最左、最右点），最低点Ⅲ、Ⅳ（也是最前、最后点）。根据各点的H面、W面投影可直接找出V面投影1′、2′、3′、（4′）［见图 1-50（a）］。

（2）作相贯线上一般点的投影。与求截交线一样，可根据连接的需要作出适当数量的一般点。在相贯线的W面投影上任取对称的5″、（6″）或7″、（8″）两个点，根据投影关系可作出H面投影 5、6、7、8，最后找 V面投影 5′、6′、（7′）、（8′）［见图 1-50（b）］。

（3）连线。根据H面投影的顺序，依次光滑连接各点的V面投影，即得所求的相贯线。

图1-51所示为圆柱穿孔三视图，其相贯线的画法与上述两圆柱面相交的画法相同。

2.相贯线的简化画法

当两圆柱正交且直径相差较大，其相贯线又不需要准确绘出时，可采用圆弧代替非圆曲线的简化画法，得到近似的相贯线投影，如图1-52所示，具体步骤如下：

（1）以两圆柱轮廓素线的交点1′或2′为圆心，以大圆柱的半径D／2为半径画圆弧，交小圆柱轴线于一点O。

（2）以 O为圆心、D／2为半径，自 1′至2′画圆弧。

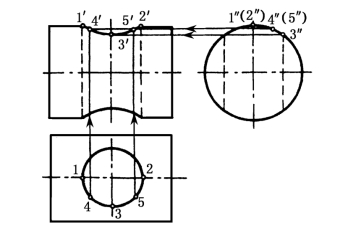
图1-51　圆柱穿孔三视图

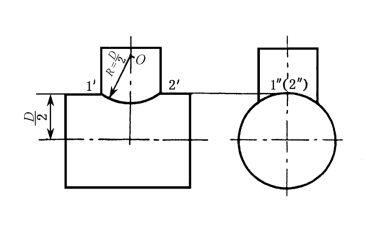
图1-52　相贯线的简化画法

3.影响圆柱相贯线的因素

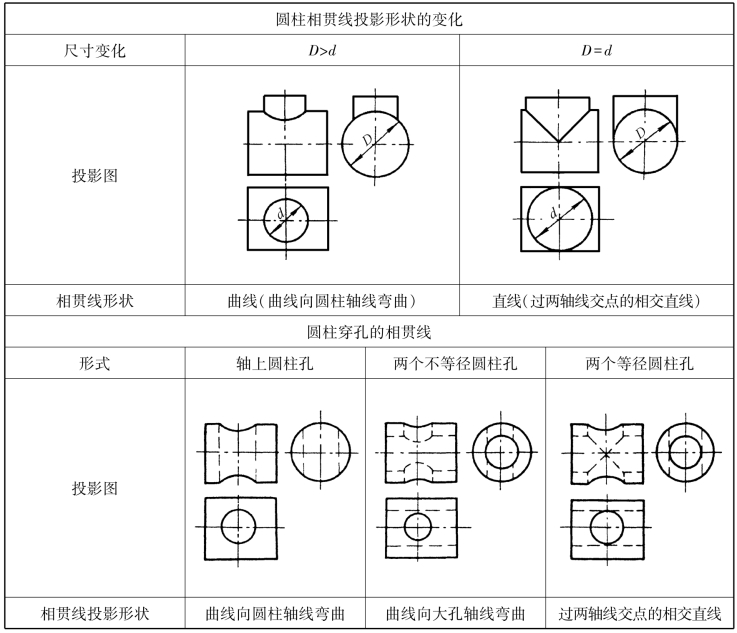
互为相贯的两个圆柱体，其直径的相对变化是影响相贯线空间形状的主要因素。因此，掌握轴线互相垂直相交的相贯线形状和变化趋势，将有利于看图和画图，见表1-11。

表1-11　影响圆柱相贯线的因素

（五）圆柱与圆球共轴相贯

如图1-53所示，圆柱与圆球具有公共轴线，相贯线是一圆（平面曲线），该圆的V面和W面投影均积聚成直线，H面投影为圆的实形。

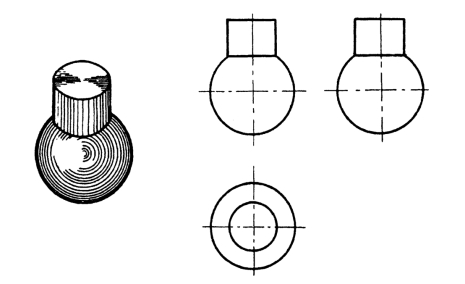
图1-53　手柄端部的投影

由图1-53可知：当两相交的回转体具有公共轴线时，其相贯线为垂直于该轴线的圆。

（六）过渡线

在铸件或锻件中，由于工艺上的要求，往往在产生相贯线的两相交表面处用一圆角圆滑地连接起来，有了圆角相贯线就不明显了，但为了读图时区分不同的表面，仍画出理论上的相贯线，这条线叫过渡线，如图1-54所示，过渡线不与圆角轮廓线接触。

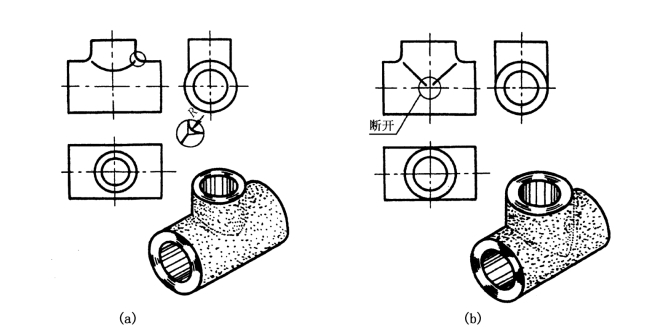
图1-54　过渡线（一）

曲面与平面相交、相切处过渡线画法及平面与平面相交处过渡线画法如图1-55所示。

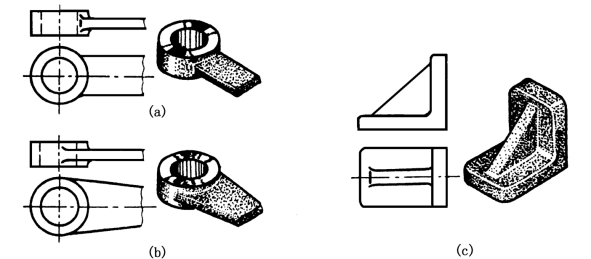
图1-55　过渡线（二）