（一）点的投影和三面投影规律

点的投影仍然是点。将空间点A置于三面投影体系中，由点A分别向V、H和W三个投影面作垂线，所得的三个垂足a′、a和a″就是点的三面投影，如图1-15所示。

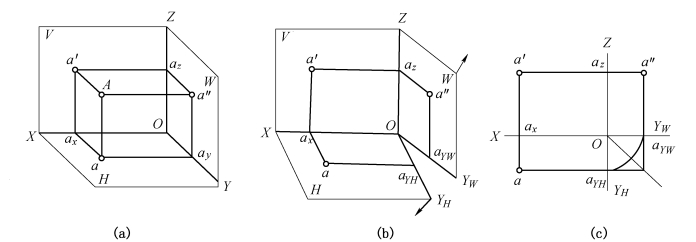
图1-15　点的三面投影图

通常规定，空间点用大写字母A，B，C…标记；水平投影用相应的小写字母a，b，c…标记；正面投影用相应的小写字母加一撇a′，b′，c′…标记；侧面投影用相应的小写字母加两撇a″，b″，c″…标记。这样A点到W面的距离为其x坐标；A点到V面的距离为其y坐标；A点到H面的距离为其z坐标。若用坐标值确定点的空间位置，则可用下列规定书写形式：

A（xA，yA，zA）、B（xB，yB，zB），如 A（25，20，30）、B（10，0，20）。

由图1-15（a）可知：Aa⊥H面，Aa′⊥V面，则通过Aa和Aa′所作的平面必然同时垂直于H面和V面，当然也就垂直于V面与H面的交线OX轴，它与OX轴的交点用ax表示。显然Aa′axa是一矩形。同理，Aa″aya和Aa′aza″也是矩形。这三个矩形平面都与相应的投影轴正交，并与相应投影面上的相应矩形围成一长方体。因为长方体中相应平行棱线长度相等，故可得点与三投影面的对应关系为：

Aa″＝a′az＝aay＝Oax（均为 x坐标）；

Aa′＝aax＝a″az＝Oay（均为 y坐标）；

Aa＝a′ax＝a″ay＝Oaz（均为 z坐标）。

由此可见，空间点在某一投影面上的投影，是由该点的两个相应坐标值所决定的。

a可由Oax和Oay，即A点的x，y两坐标决定；a′可由 Oax和 Oaz，即A点的x，z两坐标决定；a″可由 Oaz和 Oay，即 A点的 z，y两坐标决定。

如图1-15（b）所示，移去空间点A，按所规定的投影面展开方法，将三个投影面展开摊平并去掉边框线，便得到A点的三面投影图［见图1-15（c）］。为便于进行投影分析，用细实线将点的两面投影连起来得到aa′和a′a″（称为投影连线）。

当投影面展开时，H面上的一段投影连线aax随H面在垂直于OX轴的平面内旋转，所以在展开后的投影图中，a′，ax，a三点必在同一条直线上，即aa′⊥OX。同理可以说明投影连线a′a″一定垂直于OZ轴，即a′a″⊥OZ。由于Y轴展开后分别为YH和YW，故a与a″不能直接相连，需要借助45°斜线或圆弧来实现这个联系［见图1-15（c）］。

根据上述分析，可总结出点的三面投影规律：

（1）点的正面投影和水平投影的连线垂直于X轴。这两个投影都反映空间点的x坐标，表示空间点到侧投影面的距离，即 a′a⊥OX，a′az＝aaYH＝xA。

（2）点的正面投影和侧面投影的连线垂直于Z轴。这两个投影都反映空间点的z坐标，表示空间点到水平投影面的距离，即 a′a″⊥OZ，a′ax＝a″aYW＝zA。

（3）点的水平投影到X轴的距离等于侧面投影到Z轴的距离。这两个投影都反映空间点的y坐标，表示空间点到正投影面的距离，即aax＝a″az＝yA。根据点的投影规律，可由点的三个坐标值画出其三面投影图，也可根据点的两面投影作出第三面投影。

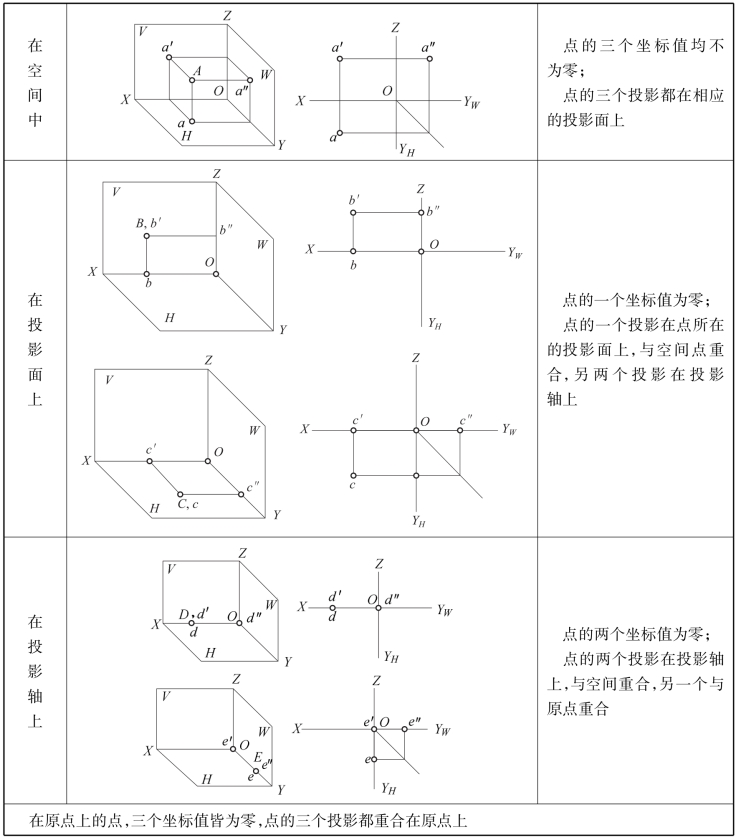
1.各种位置点的投影

各种点的位置有在空间中、在投影面上、在投影轴上、在原点上四种情况，它们在投影面上的投影各有不同的特征，见表1-5。

表1-5　各种位置点的投影图例

2.两点的相对位置

空间两点的相对位置是指它们彼此之间的方位关系，即左右、前后和上下的关系。

在三面投影体系中，两点的相对位置是由两点到三个投影面的距离，即两点的坐标差决定的。距W面远者在左，近者在右；距V面远者在前，近者在后；距H面远者在上，近者在下，如图1-16所示。

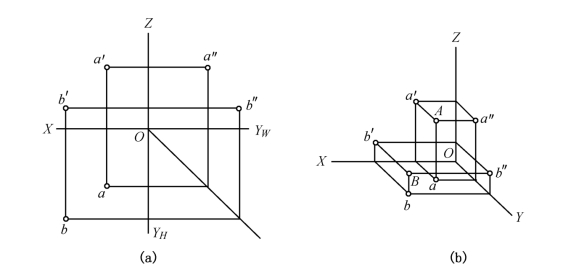
图1-16　两点的相对位置

从V、H面投影可以看出，B点比A点距W面远（xB＞xA），故B点在左、A点在右。

从V、W面投影可以看出，A点比B点距H面远（zA＞zB），故A点在上、B点在下。

从H、W面投影可以看出，B点比A点距V面远（yB＞yA），故B点在前、A点在后。

概括地说，A点在B点的右后上方，B点在A点的左前下方。

3.重影点及其可见性

当两点的某两个坐标相同时，该两点将处于对某一投影面的同一投影线上，因而在某一投影面的投影相重合，则这两点称为对该投影面的重影点。

如图1-17所示，A、B两点均在垂直于H面的同一投影线上，则它们在H面上的投影重合为一点。

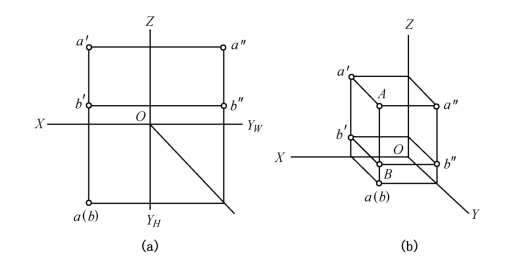
图1-17　重影点的投影

沿着投影方向，根据两点坐标的大小可以判断重影点的可见性。当两点的H面投影重合时，看其V面或W面的投影，z坐标大者可见。如图1-17所示，A点的投影a可见，B点的投影b不可见。

当两点的V面投影重合时，看其H面或W面的投影，y坐标大者可见。

当两点的W面投影重合时，看其V面或H面的投影，z坐标大者可见。

重影点在投影图上的标记规定为：将不可见点的字母用小括号括起来，如（a′）、（b）、（c″）等。

（二）直线段的正投影

空间两点确定一条空间直线段，空间直线段的投影可由线上两个点（通常指两个端点）的投影决定。

如图1-18所示，将直线段AB向H面投影，直线段上两端点A、B的同面投影a、b的连线，就是线段AB在该面上的投影。所谓同面投影，是指各几何要素在同一投影面上的投影。

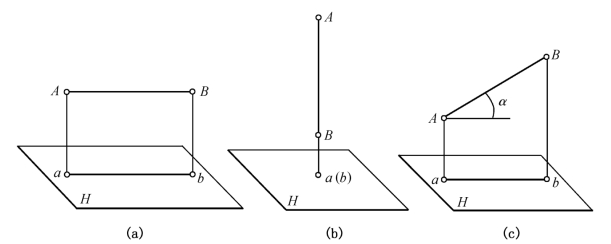
图1-18　直线段的投影

（a）真实性；（b）积聚性；（c）收缩性

1.直线段对于一个投影面的投影

空间直线段相对于一个投影面的位置有平行、垂直、倾斜三种情况，如图1-18所示。

三种不同位置直线的投影具有三种不同的投影特性。

（1）真实性：当直线段平行于投影面时，它在该投影面上的投影反映空间线段的实长。在图 1-18（a）中，ab＝AB，这种性质称为真实性。

（2）积聚性：当直线段垂直于投影面时，它在该投影面上的投影积聚成为一个点。在图 1-18（b）中，a（b）为一点，这种性质称为积聚性。

（3）收缩性：当直线段倾斜于投影面时，它在该投影面上的投影小于空间线段的实长。在图 1-18（c）中，ab＜AB，这种性质称为收缩性。

由上述可知：空间直线段的投影一般仍为直线，在垂直投影面时是一个点。

2.直线段在三投影面体系中的投影特性

空间直线段按对三个投影面的位置不同可分为三类：投影面平行线、投影面垂直线和一般位置直线。其中，投影面垂直线和投影面平行线又称为特殊位置直线。

（1）投影面平行线：平行于一个投影面，而与另外两个投影面倾斜的直线段称为投影面平行线。投影面平行线又分为以下三种：

平行于H面而与V、W面倾斜的直线叫水平线；

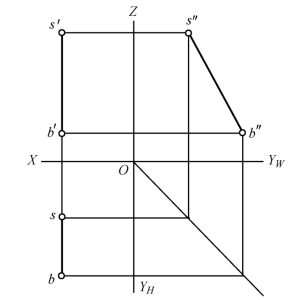
图1-19　侧平线的投影

平行于V面而与H、W面倾斜的直线叫正平线；

平行于W面而与H、V面倾斜的直线叫侧平线。

图1-19中直线为一侧平线，它的三面投影特性为：

① 侧平线的W面投影反映线段实长，即s″b″＝SB。

②侧平线的V面、H面投影分别平行于OZ、OYH轴，即 s′b′∥OZ，sb∥OYH，且小于实长 SB。

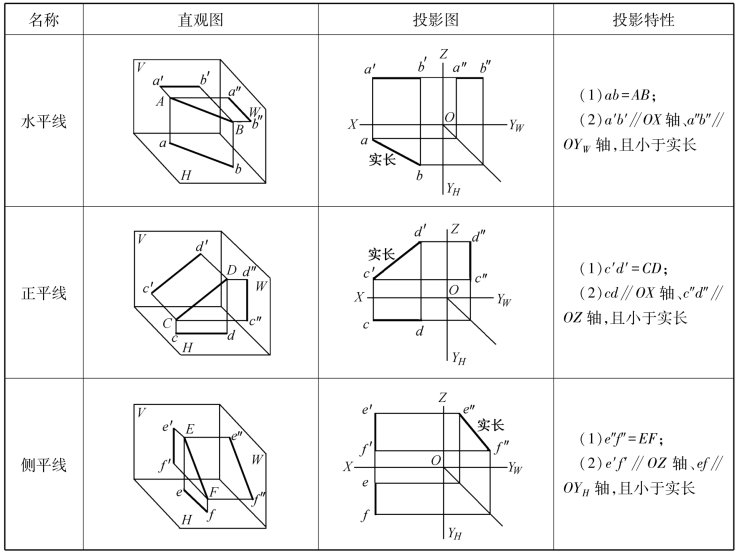
同理，也可得出水平线和正平线的投影特性，见表1-6。从表1-6中可概括出投影面平行线的投影特性：

在所平行的投影面上的投影反映实长；在另外两个投影面上的投影分别平行于直线所平行的那个投影面上的两根轴，且小于实长。

表1-6　投影面平行线的投影图例

投影面平行线的辨认：当直线段的投影有两个平行于投影轴，第三个投影与投影轴倾斜时，则该直线一定是投影面平行线，且一定平行于其投影为倾斜线的那个投影面。

（2）投影面垂直线：垂直于一个投影面，即平行于两个投影面的直线段，称为投影面垂直线。垂直于V面的直线，称为正垂线；垂直于H面的直线，称为铅垂线；垂直于W面的直线，称为侧垂线。

图1-20中AC为一侧垂线，它的三面投影特性为：

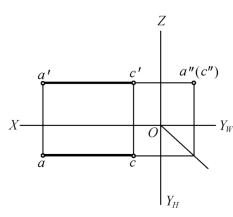
图1-20　侧垂线的投影

① W面投影 a″（c″）积聚为一点。

② V面、H面投影分别垂直于 OZ、OYH轴，即 a′c′⊥OZ，ac⊥OYH，且均反映实长，a′c′＝ac＝AC。

同理，也可得出正垂线和铅垂线的投影特性，见表1-7。从表1-7中可概括出投影面垂直线的投影特性：在直线所垂直的投影面上的投影积聚为一点；在另外两个投影面上的投影分别垂直于直线所垂直的那个投影面上的两根投影轴，且反映直线段实长。(www.daowen.com)

投影面垂直线的辨认：直线段的投影只要有投影积聚成一点，则该直线段一定是投影面垂直线，并且一定垂直于其投影积聚为一点的那个投影面。

表1-7　投影面垂直线的投影图例

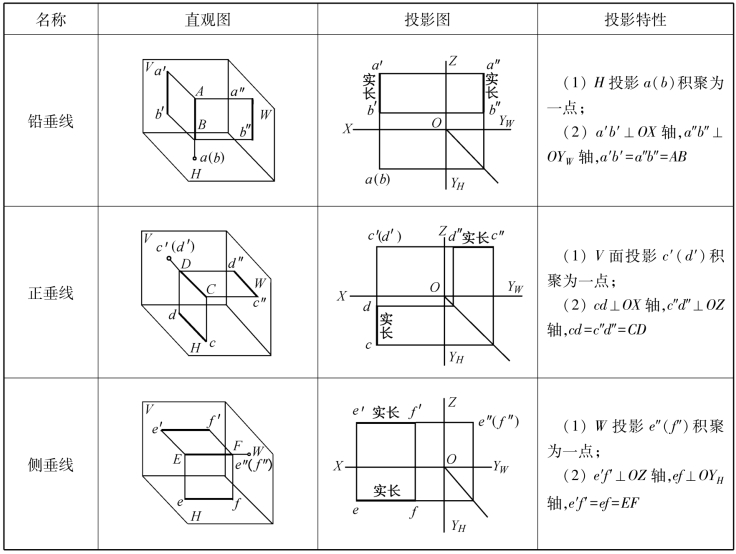
（3）一般位置直线：与三个投影面都倾斜的直线段称为一般位置直线。

如图1-21所示，直线SA对投影面V、H和W都处于倾斜位置，是一般位置直线。

一般位置直线的投影特性：

①直线的三面投影都倾斜于投影轴；

②投影的长度均小于直线段的实长。

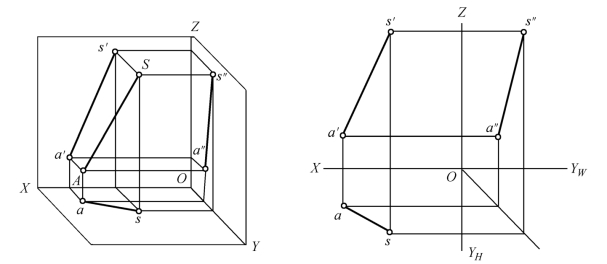
图1-21　一般位置直线的投影

一般位置直线的辨认：直线的三面投影如果与三根投影轴都倾斜，则可判定该直线为一般位置直线。

作图时，求作一般位置直线的投影也应符合“长对正、高平齐、宽相等”的投影关系。

3.图例分析

运用上述三类直线的投影特性，就可以分析一般形体上各棱线的投影，为想象立体形状打下基础。图1-22所示为一四棱截锥三面投影图，试分析图中棱线与三投影面的关系。

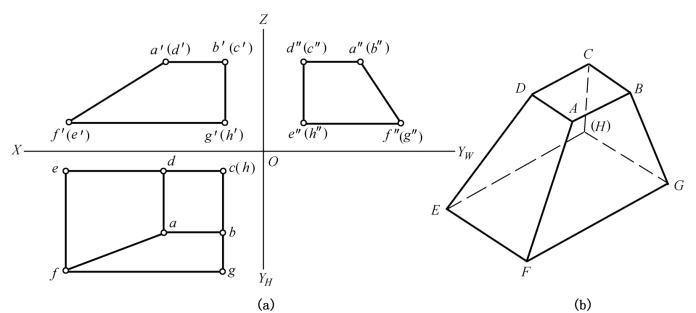
图1-22　形体中线的分析

从图 1-22（a）中可以看出棱线，AF的三面投影 af、a′f′、a″f″都与投影轴倾斜，因此棱线为一般位置直线。

棱线DE的H面投影de平行于OX轴，W面的投影d″e″平行于OZ轴，而V面上的投影d′e′与投影轴倾斜，因此DE是正平线。同理，BG为侧平线。

棱线AB的W面投影积聚为一点a″（b″），V面投影a′b′垂直于OZ轴，H面投影ab垂直于OYH轴，因此棱线AB为侧垂线。同理，DC、EH、FG也都是侧垂线。CH为铅垂线，AD、BC、FE、GH为正垂线。

通过以上分析，可以想象出该四棱截锥的形状［见图1-22（b）］。

（三）平面形的投影

形体上的任一平面形，都有其一定的形状、大小和位置。从形状上看，常见的平面形有三角形、矩形、正多边形等由直线围成的直线平面形及圆平面、椭圆面等由曲线围成的曲线平面形，还有由直线和曲线共同围成的混合平面形。将不同的平面形进行投影时，就会出现不同的形状。

平面形投影的作图方法是将图形轮廓线上的一系列点（多边形则是其顶点）向投影面投影，连线即得平面形的投影。

图1-23所示为空间三角形的三面投影图。△ABC的各面投影，实质上就是各顶点同面投影的连线。其他直线平面形的投影可用与此类似的方法求得。

综上所述，作平面形的投影，实质上仍是以点的投影为基础的。

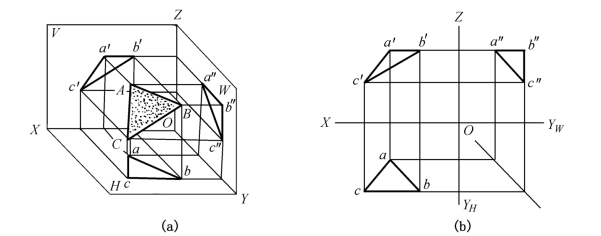
图1-23　直线平面形的投影

1.平面形对于一个投影面的投影

空间平面形相对于一个投影面的位置也有平行、垂直、倾斜三种情况，如图1-24所示。三种不同位置的平面具有三种不同的投影特性。

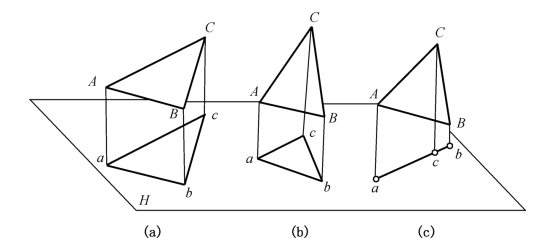
图1-24　平面投影的性质

（a）真实性；（b）收缩性；（c）积聚性

（1）真实性：当平面形平行于投影面时，它在该投影面上的投影反映空间平面形的真实形状和大小，如图1-24（a）中△abc＝△ABC，这种性质称为真实性。

（2）收缩性（类似性）：当平面形倾斜于投影面时，它在该投影面上的投影与原图形类似（即不相等，也不相似），且面积变小，如图1-24（b）中三角形投影仍为三角形，但 S△abc＜S△ABC，这种性质称为收缩性，亦称类似性。

（3）积聚性：当平面形垂直于投影面时，它在该投影面上的投影积聚成一条直线段，如图1-24（c）中△abc投影成一条直线段，这种性质称为积聚性。

由上述可知：平面形的投影一般仍为平面形，垂直投影面时是一条直线。

2.平面形在三投影面体系中的投影特性

空间平面形按对三个投影面的位置不同可分为三类：投影面垂直面、投影面平行面和一般位置平面。其中，投影面垂直面和投影面平行面又称为特殊位置平面。

（1）投影面垂直面。垂直于一个投影面，而与另外两个投影面倾斜的平面称为投影面垂直面。投影面垂直面又分为三种：

垂直于V面，而与H、W面倾斜的平面叫作正垂面；

垂直于H面，而与V、W面倾斜的平面叫作铅垂面；

垂直于W面，而与V、H面倾斜的平面叫作侧垂面。

某一平面△SAC为一侧垂面，它的三面投影如图1-25所示，其特性为：

图1-25　侧垂面的投影

① W面投影积聚成一条直线段 s″a″（c″），该线段倾斜于OZ、OYW轴。

② V面与 H面投影均比实形小，即：S△s′a′c′＜S△SAC，S△sac＜S△SAC，为类似形。

同理，也可得出铅垂面、正垂面的三面投影特性，见表1-8。由表1-8可概括出投影面垂直面的投影特性：在所垂直的投影面上的投影积聚成一条直线段，且与投影轴倾斜；在另外两个投影面上的投影均为小于原平面形的类似形。

表1-8　投影面垂直面的投影图例

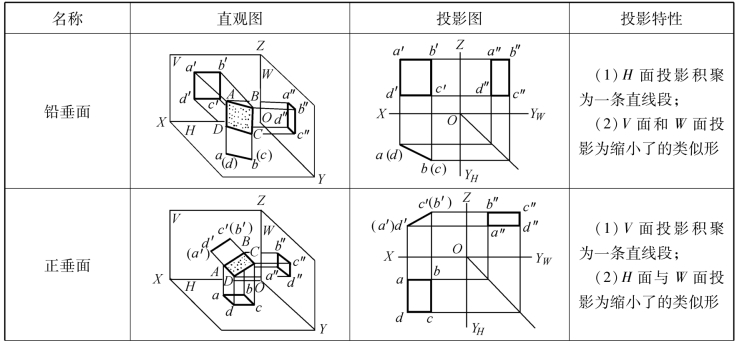
续表

投影面垂直面的辨认：如果平面形在某一投影面上的投影积聚成一条倾斜于投影轴的直线段，则该平面形一定是投影面垂直面，且一定垂直于其投影为直线段的那个投影面。

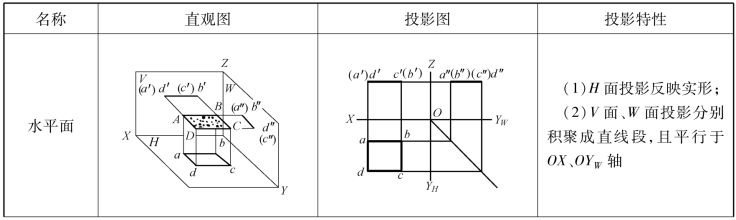
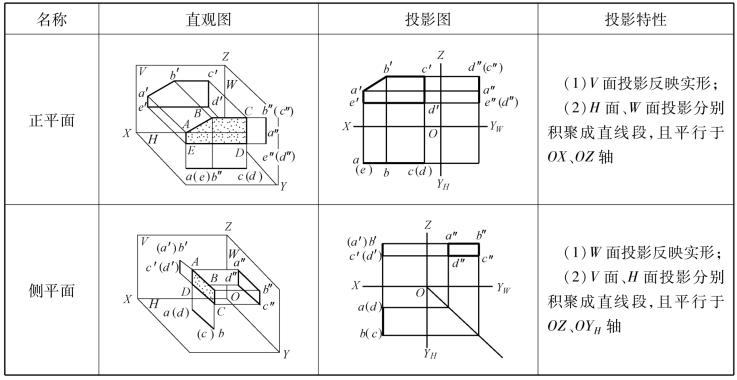
（2）投影面平行面。平行于一个投影面，即垂直于另两个投影面的平面称为投影面平行面。平行于V面的称为正平面；平行于H面的称为水平面；平行于W面的称为侧平面。

图1-26中平面△ABC为一水平面，它的三面投影特性为：

①H面投影反映实形，△abc＝△ABC。

②V面和W面投影各自积聚成一条直线段，并 分 别 与 OX、OYW 轴 平 行，即 a′b′c′∥OX，a″b″c″∥OYW。

同理，也可得出正平面和侧平面的投影特性，见表1-9。由表1-9可概括出投影面平行面的三面投影特性：平面在所平行的投影面上的投影反映实形；在另外两个投影面上的投影分别积聚成直线段，并平行于相应的投影轴。

投影面平行面的辨认：如果在平面形的投影图中，同时有两个投影分别积聚成平行于相应投影轴的直线，而另一投影为平面形，则此平面平行于该投影所在的那个投影面，平面在该投影面上的投影反映实形。

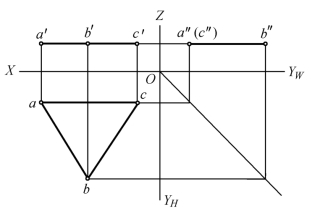
图1-26　水平面的投影

表1-9　投影面平行面的投影图例

续表

（3）一般位置平面：与V、H和W三个投影面都倾斜的平面称为一般位置平面。如图1-23中△ABC对V、H和W面都处于倾斜位置。它的三面投影既不积聚成直线段，又不反映实形，且面积缩小。

一般位置平面的投影特性：三面投影均不反映实形，且均为缩小了的类似形。

一般位置平面的辨认：如果平面的三面投影都是类似的几何图形，则该平面一定是一般位置平面。

3.图例分析

运用上述三类平面形的三面投影特性，就可分析出图1-27所示形体上各平面相对于投影面的空间位置。

图1-27所示为一个由五个平面形围成的形体，其顶面为△ABC，底面为△DEF，三侧面为四边形BCEF、ABFD和ACED。

△ABC的三面投影都是类似的三角形，分别是△abc、△a′b′c′和△a″b″c″，因而可以确认△ABC是一般位置平面。

△DEF的 V面投影为直线段 d′e′f′，d′e′f′∥OX轴；W面投影为直线段 d″f″（e″），d″f″（e″）∥OYW轴；H面投影为△def。可以判定△DEF是水平面，水平投影反映△DEF的实形。

四边形 BCEF的侧面投影 b″c″（e″）f″是与 OZ轴倾斜的直线段，H面和 V面投影 bcef、b′c′e′f′为类似形，可以判定BCEF为侧垂面。

四边形 ACED的三面投影 aced、a′c′e′d′和 a″c″（e″）d″均为类似形，可以判定四边形 ACED是一般位置平面。同时，也可判定四边形ABFD也是一般位置平面。