1.资本市场线

资本市场线（Capital Market Line，CML）属于较为特殊的CAL，其还是一条由无风险资产出发的、与有效前沿下切的切线。不过其与有效前沿应当满足下列条件，即：

（1）它涵盖了全世界上全部的风险资产。

（2）所有投资者对这些风险资产的预期都是一致的。

基于以上两个前提假设，都自认全部将拥有同一有效前沿。无风险资产与这一仅有的有效前沿组合而成的CAL即为CML，因为市场有效前沿仅有一条，所以，切点位置的最优风险组合也是市场组合，如图6-11的M点。它表示这一投资组合以0%配置于无风险资产，以100%配置于市场组合。

由于市场组合中涵盖全部风险资产在内，因此，它也属于风险被完全分散的组合。而分散掉的单一风险资产独有的风险，即为非系统风险，另一无法分散的风险即为操作系统风险。

CML上各个点的预期收益都可通过以下公式表示：

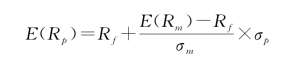
这里的E（Rp）为任意组合的预期收益率，投资组合标准差以σP表示，E（Rm）即为市场预期收益率，无风险收益率以Rf来表示。市场组合的夏普比率以CML的斜率来表示。

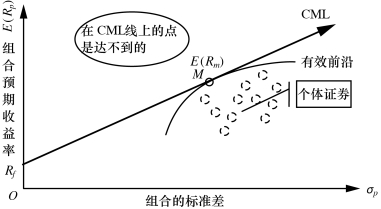
图6-11　资本市场线

2.系统性风险和非系统性风险

1）系统性风险

系统性风险属于无法被分散的风险，也叫市场风险。因为宏观因素的改变，使得整体经济环境发生改变。这些宏观因素，比如通货膨胀、利率以及政策和经济周期等，都属于系统风险。如果这些因素出现变化，则市场参与者是非常被动的。

2）贝塔值（β）

β表示任意资产i的收益率Ri受市场组合收益率Rm影响的程度。因为资产收益率与其系统性风险密切相关，所以，β也可表示资产i的系统性风险受市场组合系统性风险影响的敏感程度。资产i的系统性风险即为其收益率与市场组合收益率的协方差cov（Ri，Rm）再和市场组合的系统性风险相除所得，也就是市场回报自身的协方差cov（Rm，Rm）。因此，可通过以下公式来对任意资产i的β值进行计算：

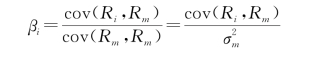
或

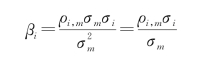
这里的Rm表示市场组合的收益率，即为市场组合收益率的方差，资产i的收益率以Ri表示，ρi，m为Ri与Rm的相关系数。

基于以上公式中能够得出下列几项结论：

①β代表了资产的系统性风险。

②β＞0，即资产收益率与市场收益率的变化方向一致；若β＜0，则资产收益率与市场收益率的变化方向相反。

③因为市场组合自身的协方差和其方差相同，所以，市场组合的β=1。

④资产的β＞1，表示对比市场组合来说，其系统性风险更大，可以理解为，对比市场组合来看，其收益率的波动更大（也就是敏感度更高）；0＜β＜1，对比市场组合来说，其系统性风险更小小，收益率的波动不明显。举例来讲，如果资产的β=1.1，即市场收益率每提升1个百分点，相应资产的合理收益率将会提升1.1个百分点。

⑤涉及多个资产的组合的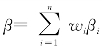，即所有资产β的加权平均值。

3）非系统性风险(www.daowen.com)

非系统风险和公司特有风险是一个概念，它是能够基于资产组合而被分散的一类风险。非系统风险仅会对某一行业或公司造成影响。

4）分散非系统性风险

方差σ2可用来表示某一资产的总风险。总风险中涵盖系统风险与非系统风险在内。图6-12表示的未风险分散化的过程，该过程即为降低组合的方差或标准差的过程。由图可知，基于新资产的加入，总风险持续降低，同时，总风险中的非系统风险也在降低，最后组合中仅余系统性风险。分散效果最显著的时期为初期，几个资产加入时，基于资产数目的递增，分散化的速度也越来越慢。

3.收益率生成模型

之所以要对资产的系统性风险进行探究，主要是为了确定资产的合理预期收益率，其实也是对风险进行定价的具体过程。资产预期收益率和多方面因素有关。具体有基本面因素、宏观因素以及统计因素等，基于多种因素构建而成的收益率模型为多因子模型。仅涉及一种因素的模型即为单因子模型。

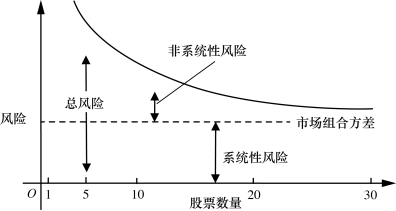
图6-12　系统性风险与非系统性风险

1）多因子模型

以下为多因子模型的表达式：

这里的βi，k代表资产i的超额收益率受某个因子k的影响，而表现出的敏感度。

这些因子可能涵盖以下三类：

（1）宏观经济因子：比如GDP的提升，利率，通货膨胀率等。

（2）基本面因子：涉及公司的基本面因素，具体有利润增长、利润，以及研发经费和广告费用、专利等。

（3）统计因子：基于对历史收益率进行统计分析，找到能够对影响收益率波动进行解释的因子。在统计部分，这些因子是有意义的，不过并不一定在现实中有意义，并且也可能涉及数据挖掘方面的问题。

2）单因子模型

单因子模型将市场风险当作仅有的资产收益率影响因素，公式为

上式为任意资产i的预期收益率的表达式，需要关注的是，此时资产i并非一定是风险完全分散化的，我们仅针对资产i涉及的系统性风险（用βi衡量）得到一个预期收益率，即

对风险完全分散化的资产组合（即位于CML上的组合）展开深入探讨，将上述两个公式进行对比，能够发现风险完全分散化的组合的β=σp/σm，由此说明，CML与一个风险完全分散化组合的预期收益率的单因子模型是一致的。

市场模型即为单因子模型的另一应用。以下为市场模型的表达式：

Ri=ai+βiRm+ei

通过市场模型，我们可以得到系统性风险β。在对资产i的历史收益率Ri和市场组合的历史收益率Rm展开线性回归（图6-13），该回归线即为证券特征线（Security Characteristic Line，SCL），该线的斜率为β，其在y轴的截距即为a，实际数据与回归线之间的差异即为误差项e。

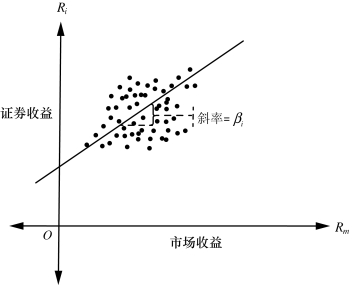
图6-13　证券特征线