1.组合的收益与风险

一个投资组合最少应涉及两个资产，所以先探究两个风险资产的组合。

1）两个风险资产的组合的收益

组合的收益率，即组合内各项资产收益率的加权均值。针对两个资产的组合，公式表示为

Rp=w1R1+(1-w1)R2

这里的w1为资产1的权重，也就是资产1的价值在整体组合价值中的占比；R1表示资产1的收益率；1-w1为资产2的权重；R2代表资产2的收益率。

2）两个风险资产的组合的风险

组合的风险也是组合收益的不确定性，通过组合标准差来进行判定。以下为两个风险资产的组合标准差：

或是

这里的cov（R1，R2）代表资产1、2的收益率协方差，ρ1，2为资产1、2的收益率的相关系数。

通过以下公式可以对两个资产收益率协方差与相关系数进行计算：

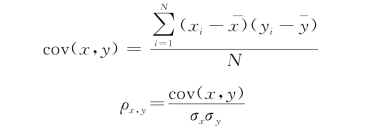
这里的N为个体数量。

以下具体分析ρ1，2为组合标准差带来的影响。

（1）若ρ=1，资产1与2的收益率完全线性正相关，收益率移动的方向是相同的，这时组合的标准差为：

因此，组合的标准差即为两个资产的标准差的加权平均值，组合收益率为两个资产的收益率的加权平均值：

Rp=w1R1+w2R2（和ρ1，2无关）

这种情况下产生的组合效果与之前的单独资产是一致的，将两个完全正相关的资产放在一起，是无法发挥规避风险的效果的。

（2）若ρ＜1，资产1与2的收益率并非完全线性正相关，组合的标准差表示如下：

能够发现组合的风险被缩减了，由此也实现了分散风险的效果。

在已知两个资产收益率相关系数p的情况下，基于更改两个资产的权重wA、wB，我们获取到一系列新组合。由图6-5可知，A点为资产A（组合里wA=100%，wB=0%），B点指的是资产B（组合里wB=100%，wA=0%）。如果A与B的ρ为1，则它们基于不同权重形成的一系列新组合将会在连接AB两点的直线上。如果ρ＜1的，这一系列组合构成的是一条曲线（即图6-5中虚线，ρ的值发生变化，虚线弯曲度也将改变）。若ρ=-1，则这一系列组合将构成一条折线。

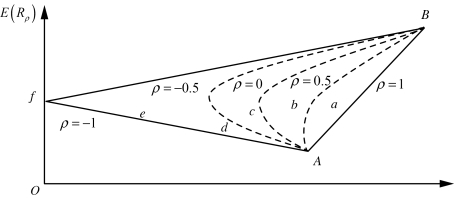
图6-5　组合的收益-风险关系

由图6-5能够总结几项重要结论：

①在相关系数不断减小的情况下，保持组合收益率不变，组合风险将不断减少（a、b、c、d、e分别表示收益率一样、风险陆续降低的组合）。(www.daowen.com)

②如果两个资产ρ＜1，基于对权重进行适当分配，能够得到一个风险低于之前的单独资产风险的更小组合，即图中c、d点表示的组合，它们的标准差比σA、σB都小。

③两个资产ρ=-1的情况下，形成一系列组合，即与y轴相交的两条直线，交点f表示一个无风险组合，σP为0。

2.资本配置线

有效前沿仅表示一系列风险资产形成的组合，而实践中还存在无风险资产。因此，需要关注无风险与多个风险资产形成的组合的问题。

1）无风险资产和单个风险资产组合的资本配置线（CAL）

无风险资产的收益率标准差是0，同时，无风险资产与风险资产的相关系数同样是0，把这两条重要性质引入组合的收益率与标准差的公式中，可得出以下公式：

Rp=w有风险R有风险+w无风险R无风险

σp=w有风险σ有风险

在对上述两个公式进行整理变形后，可归纳出组合的收益和风险之间的关联性：

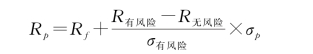
CAL的截距为无风险收益率，其斜率是夏普比率。能够发现，这是组合收益与风险为线性关系，可通过图形来表示，具体为图6-6，横轴为组合风险，也是标准差，纵轴为组合预期收益，也是各个资产预期收益的加权均值。全部组合点位于无风险资产与风险资产的连线上，该线即为资本配置线（CAL），组合点离无风险资产越近，就说明组合中的无风险资产比重越大。反之，同理。某点落于风险资产以上部分（图6-6中A点）的情况下，也表示组合中的风险资产比例高于100%，无风险比例为负。这种情况下，投资者基于无风险利率借钱投入到风险资产中，在组合内使用杠杆。同时，我们还需要关注该直线的斜率为这一风险资产的夏普比率。

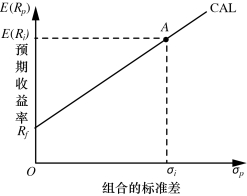
图6-6　资本配置线

2）CAL上的最优组合

由于我们的最终诉求就是要找到能够最大程度上提升投资者效用的组合，因此，可结合投资者的无差异曲线，并基于“效用最大化”的原则在CAL上确定一个符合投资者需求的组合。

在图6-7中，曲线1的效用较高，不过其与CAL无交点。b、m、a都落在CAL上的，而其中m点效用最高，为最佳组合点。因此，最优组合点即为效用曲线与CAL的切点，也就是图上的m点。这就是为投资者最优投资组合。

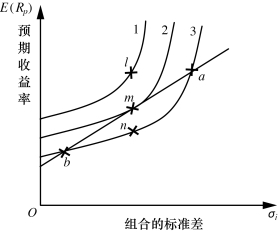
图6-7　效用曲线与CAL

因为不同的投资者对风险的厌恶程度不同，所以最终的无差异曲线也不同。由此，以下两位投资者，一位A为4，另一位A为2，相对于后一投资者来说，前一投资者对风险是更加厌恶的（图6-8）。表现为对风险更为厌恶的投资者，其效用曲线是相对更陡峭的，而这一投资者的最优投资组合也是收益与风险相对较低的点。由此，风险厌恶程度不高的投资者，其最优投资组合将会是收益与风险都相对更高的组合。

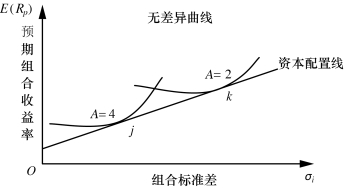
图6-8　不同投资者的效用曲线与CAL

3）最优CAL

市场上的风险资产有很多，各个风险资产都能够与无风险资产结合构建一条CAL。如图6-9中A、B、C为三个不同的风险资产，在其各自的CAL中，CAL（C）位最优的CAL。这是因为，不管风险程度怎样，CAL（C）的预期收益率都在三条线中为最大的。

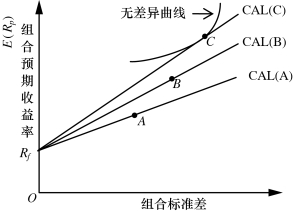
图6-9　最优资本配置线

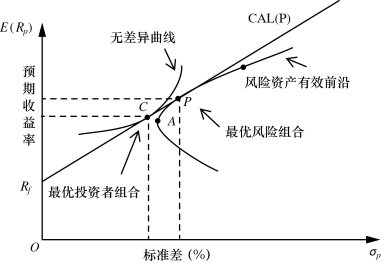
图6-10　最优风险组合和最优投资者组合

在实际的操作中，投资者可以接触到的风险投资有多种，因此，我们要找的最优组合即为涵盖无风险资产与多个风险资产的组合。无风险资产形成的组合又是有效前沿，因此，由无风险资产开始，与有效前沿相切的切线即为最优CAL，见图6-10。与前文切点为单个风险资产是有区别的，这里的切点P为风险资产组合，也是最优风险组合，投资者的效用曲线与CAL的切点C，即为最优投资人组合C点表示的组合是P与无风险资产共同组成的。C点中所有资产的配比即为资产配置需要得到结果。