【学习要求】

1.通过实验，理解密度.

2.记住水的密度.能解释生活中一些与密度有关的物理现象.

3.会测量固体和液体的密度.

【知识网络】

【知识要点】

1.密度的定义

在物理学中，把某种物质的质量与该物质体积的比叫做这种物质的密度.密度是物质的一种物理属性，它的大小由这种物质本身决定，而与这种物质的形状、大小无关.每种物质都有一定的密度，不同物质的密度一般是不同的.

密度的计算公式：

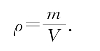
其中ρ代表密度，m代表质量，V代表体积.

在国际单位制中，质量的单位用kg，体积的单位用m3，密度的单位是kg/m3，读作“千克每立方米”.此外，常用的密度单位有g/cm3、kg/dm3.

1g/cm3=1kg/dm3=1×103kg/m3.

在计算有关密度的问题时，要注意统一单位.

记住水的密度是1.0×103kg/m3.

2.密度的测定

先测出待测物体的质量m和体积V，然后根据密度公式求出其密度.

具体方法：质量用天平测量.体积的测量视具体对象而定：对于形状规则的固体，可用几何方法测算；对于形状不规则的固体，可用量筒或量杯来测量，体积等于固体全部浸入水中时的刻度值减去固体未浸入水中时的刻度值；对于液体的体积，可直接用量筒或量杯来测量.

应当注意的是，量筒或量杯的刻度是用mL作单位的，1mL=1cm3.观察量筒或量杯里水面到达的刻度时，视线要跟水面相平.量筒和量杯里的水面是凹形的，观察时要以凹形的底部为准.

3.密度的应用

（1）鉴别物质.

（2）根据对密度的要求选择材料.

（3）计算不便直接测量的物体的质量（m=ρV）.

（4）计算不便直接测量的物体的体积.

【典型例题】

例1　关于密度公式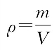，下列说法正确的是（　　）.

A.由公式可知，ρ与m成正比，m越大，ρ越大

B.由公式可知，ρ与m成反比，m越大，ρ越小

C.由公式可知，当物质的质量m一定时，ρ与V成正比，当物质的体积一定时，ρ与m成正比

D.由公式可知，物质的质量m与物质的体积V的比值是定值

点拨　本题考查密度这一基本概念，要求学生正确理解密度概念，明确密度是物质的一种特性，它不会由于物体的质量或体积的改变而改变.

例2　将一金属块A放入盛满酒精的杯中，有8g酒精从杯中溢出；将另一金属块B放入盛满水的杯中，溢出水的质量也为8g.求金属块A、B的体积之比.（已知ρ酒精=0.8×103kg/m3）

点拨　金属块A的体积与溢出酒精的体积相等，金属块B的体积与溢出水的体积相等，而溢出的酒精和水的质量是相等的，从而可求出金属块A、B的体积之比.

例3　质量相等、半径相同的空心铜球、铁球和铝球各一个（ρ铜＞ρ铁＞ρ铝），则空心部分体积最大的球是（　　）.

A.铜球　　B.铁球　　C.铝球　　D.条件不足，无法确定

点拨　利用密度判断物体空心或实心情况有下列几种方法：（1）用公式求物体的平均密度，若ρ物体=ρ物质，球为实心，ρ物体＜ρ物质，球为空心.（2）用公式求出物体中含物质的体积，若V物质=V实际，球为实心，V物质＜V实际，则球为空心.

例4　一空瓶质量是200g，装满水后称出瓶和水的总质量是700g，将瓶中水倒出，先在空瓶内装一些金属颗粒，称出瓶和金属颗粒总质量是1090g，然后将瓶内装满水，称出瓶、水和金属颗粒的总质量是1490g，求瓶内金属颗粒的密度是多少？可能是什么金属？

点拨　要判断是什么金属，就要知道金属的密度，而要知道密度，就要设法算出金属颗粒的质量和体积.

例5　江苏省生产的大豆颗粒饱满、质地坚实、出油量高，在国内外市场上享有很高声誉.小明猜想这种大豆的密度一定较大.为此，他请教了张大伯.张大伯说：“你的猜想是正确的.”同时又告诉他，“这种大豆的密度比水的密度大，但具体的数值还需要你自己去测定.”于是，小明找来天平（附砝码）、量筒和适量的水，请你帮他设计一个实验，其要求是：

（1）写出测量步骤及大豆密度的表达式.

（2）写出操作中为了减小误差而需注意的事项（写两项）.

点拨　实验原理是根据，用天平测出m，用量筒和适量的水测出V，产生误差的主要因素是：大豆是否干净，大豆中是否有气泡出现.

例6　有一团长细铁丝，用天平称出它的质量是150g，测得铁丝的直径是1mm，这团铁丝有多长？（ρ铁=7.9g/cm3）

点拨　利用密度可以解决一些不易直接测量的问题.该题中细铁丝长度不容易用刻度尺测量，但用天平测量铁丝的质量很方便，这样就可以利用密度公式求出它的体积，长度就可以计算出来.

【例题解析】

例1：密度是物质的一种特性，各种物质的密度一般是一定的，不同物质的密度一般是不同的，物质密度等于质量跟体积的比值，即，但与其质量和体积无关，所以D是正确的.

例2：根据题意可知，金属块A的体积与溢出酒精的体积相同，即

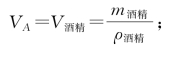
金属块B的体积与溢出水的体积相同，即

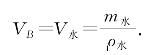
溢出的水、酒精质量相同，即　m酒精=m水，所以

将ρ酒精=0.8×103kg/m3、ρ水=1.0×103kg/m3代入，可求出金属块A、B的体积之比为

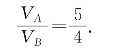
题目给出的m=8g可以不用，无须根据这个质量求出金属块A、B的体积值.

例3：根据密度计算公式，质量相等的不同物质，密度大的体积小.因为ρ铜＞ρ铁＞ρ铝，质量相等、半径相同（体积相等）的空心铜球、铁球和铝球，含有物质部分的体积最小的是铜球，所以中间空心部分体积最大的是铜球，选项A是正确的.

例4：瓶中装满水时，水的质量m水=700g-200g=500g.

查密度表可知，这种金属可能是铜.

例5：（1）用天平称适量大豆的质量，记为m，在量筒中注入适量的水，读出此时水的体积，记为V1；把称好的大豆全部倒入量筒内的水中，读出此时量筒内水和大豆的总体积，记为V2，则大豆密度表达式为.

（2）①除去瘪粒；②选用的大豆要干净；③大豆数量以倒入量筒后能全部浸没水中且便于读数为宜；④大豆倒入水中后要适当摇晃，排出气泡；⑤大豆不要在水中浸泡时间过长，再次测量要换用新的大豆；⑥不能先测体积后测质量.

例6：由，铁丝的截面积，根据V=Sl可得，.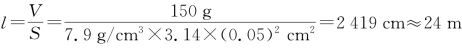

自我评估

一、填空题

1.现有由同种材料制成的A、B两金属球，其中一个是实心的，它们的质量分别为128g、60g，体积分别为16cm3、12cm3.可判断出实心球是__________（选填“A”或“B”）球，它的密度是__________g/cm3.

2.体积为0.5m3的钢瓶内装有密度为6kg/m3的氧气，某次电焊中用去了其中的，则钢瓶内剩余氧气的质量为__________kg，剩余氧气的密度为__________kg/m3.

3.甲、乙两实心金属块，甲的体积是乙的4倍，乙的密度是甲的，则它们的质量之比为　________；若将甲切去，乙切去后，甲、乙两金属块剩下部分的密度之比为____________.

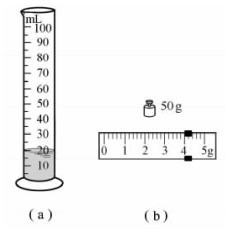
图　3-5(www.daowen.com)

4.在“测量盐水密度”的实验中：

（1）将天平放在水平桌面上，将游码移至标尺左端的“0”刻度线处，若发现指针静止时指在分度盘中央的左侧，则应将________向________（选填“左”或“右”）调节，使横梁平衡.

（2）在烧杯中倒入盐水，称出烧杯与盐水的总质量为75g.

（3）如图3-5（a）所示，将烧杯中一部分盐水倒入量筒中，则量筒内盐水的体积是________cm3.称量烧杯和剩余盐水总质量时，加减砝码总不能使天平平衡，这时应________使天平平衡.

（4）若天平再次平衡时所用的砝码、游码位置如图3-5（b）所示，则（3）中倒入量筒内的盐水质量为________g.通过计算可知盐水的密度为________kg/m3.

5.有一天，小明看到燃气公司的价格牌上写着：冬季55元/瓶，夏季51元/瓶.他寻思着，为什么夏季价格低？他查找了有关燃气的资料，燃气在冬季的密度约为0.44×103kg/m3，夏季的密度约为0.4×103kg/m3，燃气瓶容积为0.015m3.通过计算发现夏季价格比冬季价格__________（选填“高”或“低”），若燃气在夏季价格与冬季价格一样，则夏季每千克应标价为__________元.

二、选择题

6.下列现象中，物质的密度发生变化的是（　　）.

A.一杯水倒掉一半　　B.一块铁热胀冷缩

C.一块玻璃打碎了　　D.粗铜丝变成细铜丝

7.恒星在演化过程中会形成密度很大的天体，如白矮星、中子星或黑洞.据推测，1cm3中子星物质的质量是1.5×109t，则中子星的密度约（　　）.

A.1.5×1012kg/m3　　B.1.5×1015kg/m3

C.1.5×1018kg/m3　　D.1.5×1021kg/m3

图　3-6

8.甲、乙两种物质的m-V图像如图3-6所示，分析图像可知（　　）.

A.若甲、乙的质量相等，则甲的体积较大

B.若甲、乙的体积相等，则甲的质量较小

C.两物质的密度之比为4∶1

D.两物质的密度之比为1∶4

9.甲、乙两物体的质量之比为3∶2，体积之比为1∶3，那么它们的密度之比为（　　）.

A.1∶2　　B.2∶1　　C.2∶9　　D.9∶2

10.不漏气的橡皮氢气球由地面上升过程中，下列关于球内气体的质量与密度的说法，正确的是（　　）.

A.质量不变，密度增加　　B.质量不变，密度减小

C.质量增加，密度不变　　D.质量减小，密度不变

11.小花同学利用天平和量杯测量某种液体的密度时，记录实验的数据如下表.这种液体的密度和空量杯的质量分别是（　　）.

A.3.0×103kg/m3　10g　　B.1.7×103kg/m3　10g

C.1.4×103kg/m3　20g　　D.1.0×103kg/m3　20g

12.甲物质的密度为5g/cm3，乙物质的密度为2g/cm3，各取一定质量混合后密度为3g/cm3.假设混合前后总体积保持不变，则所取甲、乙两种物质的质量之比是（　　）.

A.5∶2　　B.2∶5　　C.5∶4　　D.4∶5

三、实验和设计题

13.在探究“物体的质量与体积之间的关系”时，小明同学把收集到的数据填入下表.但他漏填了第2次测量的质量和体积，其质量和体积的示数如图3-7所示.

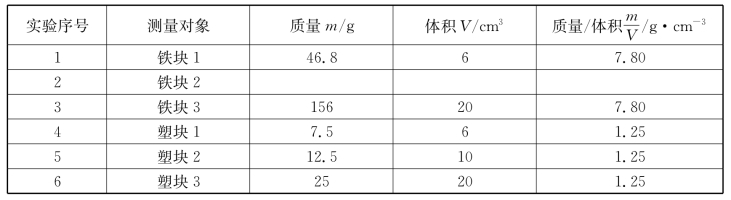
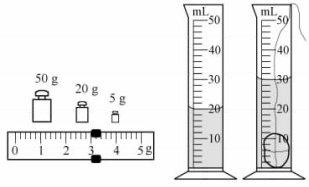
图　3-7

（1）请你帮他完成表格中漏填的三个数据：________、　_______、________.

（2）分析表格中的数据，可得出的结论：_________________________.（写出一个即可）

（3）小明与其他同学交流后，发现从表中的数据可以看出：由同种物质组成的不同物体，其质量与体积之间存在一个关系，请写出此关系.________________________________.

14.社会上食品造假事件时有发生.小明的奶奶从自由市场上购买了一箱牛奶，小明想知道牛奶是否掺水.通过查阅资料得知，在牛奶中掺水后，掺水含量与牛奶密度的关系如下表所示.小明取100mL这种牛奶，测得它的质量为102.2g，则这种牛奶（　　）.

A.未掺水　　B.掺水含量20%以下

C.掺水含量20%～30%　　D.掺水含量30%以上

15.小明测量雨花石的密度，进行了如下实验.

（1）将天平放在__________桌面上，游码放在标尺左端零刻度线处，发现指针静止时如图3-8（a）所示，应将天平的平衡螺母向_____________端调节，使横梁平衡.

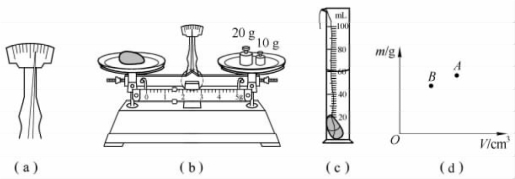
图　3-8

（2）如图（b）所示，雨花石的质量为__________g.

（3）将雨花石放入盛有50mL水的量筒中，静止时液面情况如图（c）所示，则雨花石的密度是__________kg/m3.

（4）小明根据所测数据，在图（d）上描出一个对应的点A，接着他又换用另一石块重复了上述实验，将所测数据在图（d）上又描出了另一个对应的点B.若ρA、ρB分别代表雨花石和另一石块的密度，则ρA__________________（选填“＞”“=”或“＜”）ρB.

16.在已知空气密度ρ空气的前提下，要测量一墨水瓶中空气的质量，现有器材为天平（附砝码）、水、空墨水瓶.

（1）此题关键是测量盛满水的墨水瓶中水的________，算出水的________，从而知道瓶的容积V瓶.

（2）写出空气质量m空气的表达式.

17.在测定植物油密度的实验中，小月同学按照正确的实验方法和步骤进行操作，并设计了如下记录数据的表格.

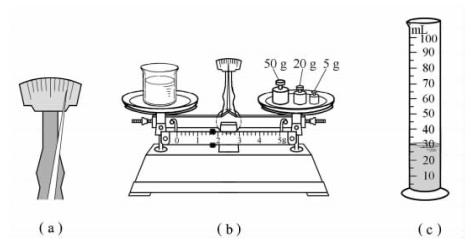
图　3-9

（1）小月将托盘天平放在水平桌面上，接下来的操作是____________，发现指针静止时如图3-9（a）所示，这时她应将横梁右端的平衡螺母向________（选填“左”或“右”）调节，使天平平衡.

（2）如图3-9（b）所示是将烧杯中的部分植物油倒入量筒后，置于调平的天平上，天平重新平衡时的情境；如图3-9（c）所示是将烧杯中部分植物油倒入量筒后的情境.请根据图中情景帮小月将下表填写完整.

（3）另一位同学的实验方法是：先测出空烧杯的质量为m1；再用量筒测出适量植物油的体积V，接着将量筒中的植物油倒入烧杯后，测出总质量为m2；然后计算出植物油的密度ρ′.与小月测出的植物油密度ρ相比较，则ρ′________（选填“＜”“＞”或“=”）ρ.

四、计算和应用题

18.今年小明家种植柑橘获得了丰收.小明想：柑橘的密度是多少呢？于是，他将柑橘带到学校实验室，用天平、溢杯来测量柑橘的密度.他用天平测出一个柑橘的质量是114g，测得装满水的溢杯的总质量是360g.然后他借助牙签使这个柑橘浸没在溢杯中，当溢杯停止排水后再取出柑橘，接着测得溢杯的总质量是240g.请根据上述实验过程解答下列问题：

（1）溢杯中排出的水的质量是多大？

（2）这个柑橘的体积和密度各是多少？

（3）小明用这种方法测出的这个柑橘的密度与它的实际密度比较，是偏大还是偏小？

19.纯牛奶的密度为（1.1～1.2）×103kg/m3，李明很想知道学校每天营养餐中提供的牛奶是不是纯牛奶.他和几个同学根据所学密度知识进行了如下测定：首先用天平称出一盒牛奶的质量是250g，喝完再称得空盒质量是26g，然后认真观察牛奶盒，发现牛奶的净含量是200mL.问：经他们检测计算，同学们喝的牛奶是否符合纯牛奶标准？

20.盐水选种是我国古代劳动人民发明的一种挑选种子的方法，选芒粳稻种需要配制密度为1.1×103kg/m3的盐水.所配制的盐水是否符合要求，可采用取样分析的方法来判别.设取500mL的盐水样品，称得其质量为600g.

（1）请分析这样的盐水是否符合选芒粳稻种的要求.

（2）若不符合要求，应加盐还是加水？