（一）概念

指数平滑法又称指数加权平均法，是选取各时期的权重数值为递减指数数列的均值方法，实际上是加权移动平均法的一种变化。它解决了移动平均法需要n个观测值和不考虑t-n前时期数据的缺点，通过某种平均方式，消除历史统计序列中的随机波动，找出其中的主要发展趋势。

指数平滑法有一次指数平滑法、二次指数平滑法、三次指数平滑法和高次指数平滑法，这里只介绍一次指数平滑法。

（二）一次指数平滑法

一次指数平滑法是只对时序数列进行一次平滑处理，将本期指数平滑值作为下期预测值的预测方法。与简单移动平均法相似，都能够提供简单适用的预测。不同的是，简单指数平滑法对先前预测结果的误差进行了修正。

该法适用于市场观测呈水平波动，无明显上升或下降趋势情况下的预测。

1.一次指数平滑法的步骤

1）对时间序列数据进行一次指数平滑处理。

对时间序列x₁，x₂，…，x_t，其公式为

F_t=αx_t+（1-α）F_t-1

式中α——平滑系数，0<α<1；

x_t——历史数据序列x在t时的观测值；

F_t，F_t-1——t时和t-1时的平滑值。

2）将本期指数平滑值作为下期的预测值x′_t+1，预测模型为：x′_t+1=F_t。

结合平滑公式，预测模型可写成

x′_t+1=αx_t+（1-α）x_t′

2.一次指数平滑法的说明

（1）平滑系数α的确定。α越接近1时，说明近期观测值对预测值影响较大，即对近期影响变量因素的作用考虑较多，对预测值误差的修正作用就越大；当α=1时，本期预测值等于前一期观测值；当α接近于0时，对预测值误差的修正作用较小；当α=0时，本期预测值等于前一期预测值。研究表明，大的α值导致较小的平滑效果，而较小的α值会产生客观的平滑效果。

一般情况下：

1）观测值呈现较稳定的水平发展时，0.1≤α<0.3。(www.daowen.com)

2）观测值波动较大时，0.3≤α<0.5。

3）观测值波动很大时，0.5≤α<0.8。

（2）初始值F₀的确定。用指数平滑法预测，首先要确定初始值F₀，一般按下列方法处理：

1）时间序列期数在20个以上时，初始值F₀对预测结果的影响很小，可取F₀=x₁。

2）时间序列期数小于20个时，初始值F₀对预测结果有一定影响，可取前3～5个观测值的平均数代替，如。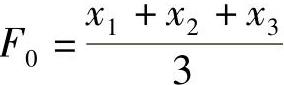

【例3-8】某家用电器商场某年1～10月份的电冰箱销售额见表3⁃10，请用一次指数平滑法预测该家用电器商场当年11月份的销售额（α=0.3）。

表3-10 某家用电器商场电冰箱销售额

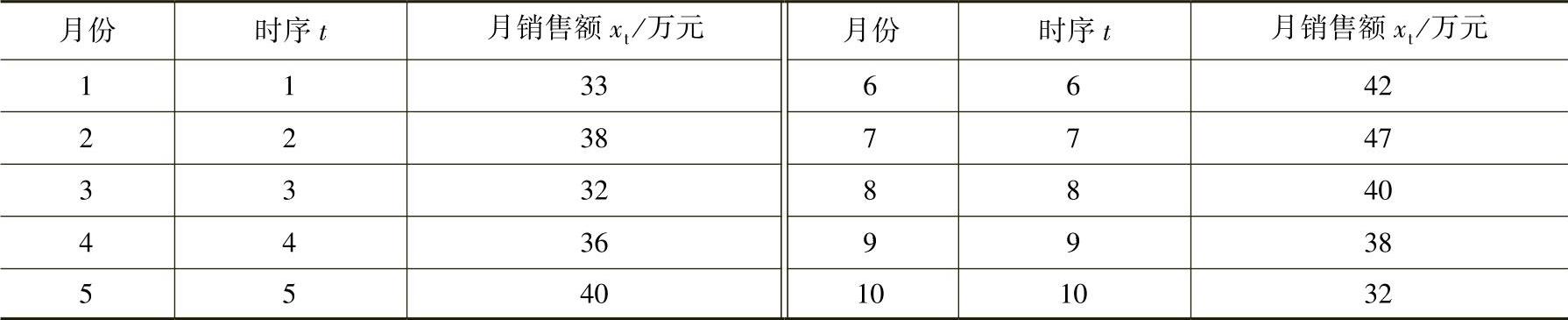
【解答】

（1）计算初始平滑值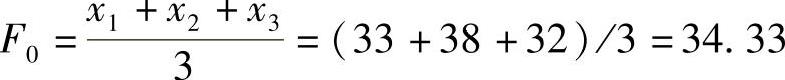：万元

（2）由指数平滑法公式

F₁=αx₁+（1-α）F₀=0.3×33+（1-0.3）×34.33=33.93万元

F₂=αx₂+（1-α）F₁=0.3×38+（1-0.3）×33.93=35.15万元

F₃=αx₃+（1-α）F₂=0.3×32+（1-0.3）×35.15=34.21万元

……

由此类推，各期指数平滑值见表3-11。

表3-11 各期指数平滑值

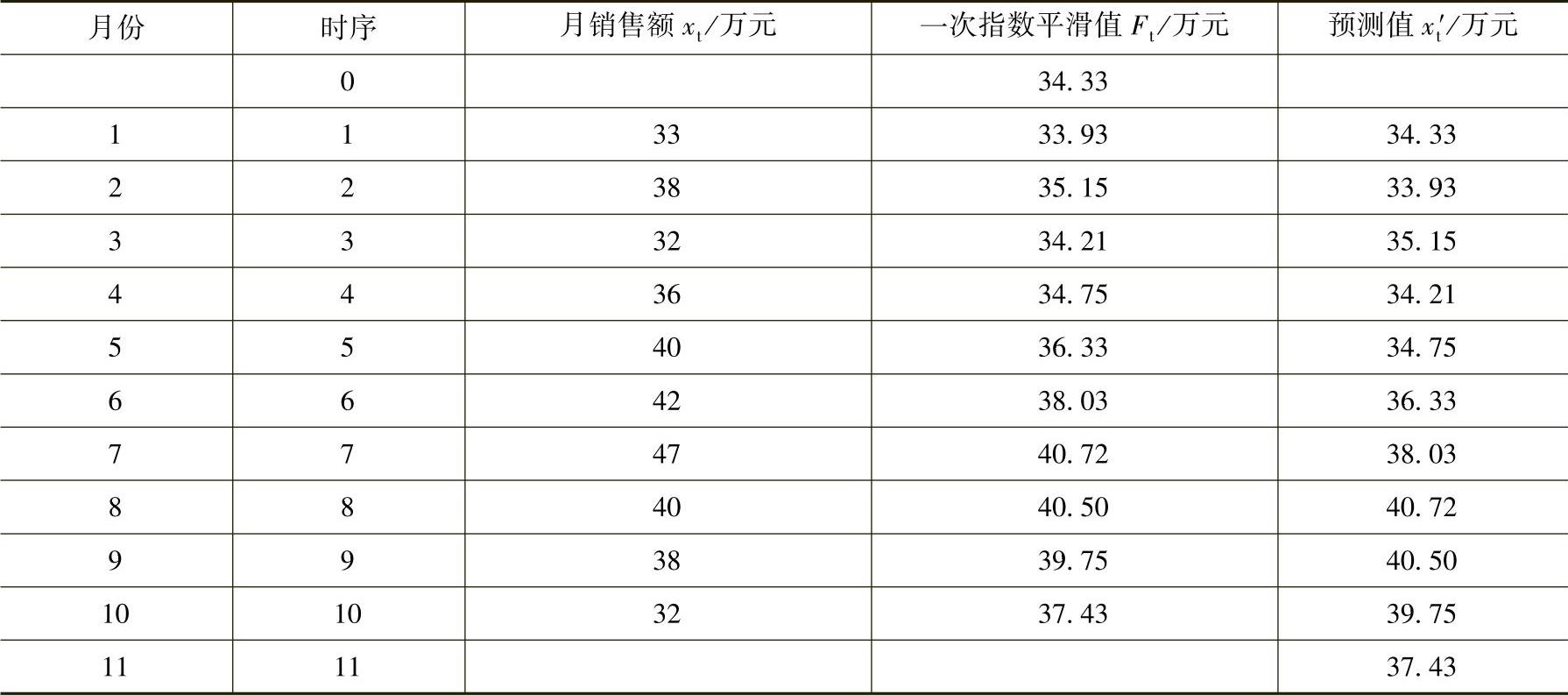
故，11月份的销售额为x₁′₁=F₁₀=37.43万元