(一)概念
移动平均法分为简单移动平均法和加权移动平均法。简单移动平均法是以过去某一段时间的数据算术平均值作为将来某时期的预测值的一种方法;而加权移动平均法是在简单移动平均法的基础上,给不同时期的变量值赋予不同的权重来计算预测值。
(二)简单移动平均法的基本原理
1.公式
简单移动平均法可以表述为: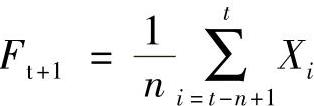
式中Ft+1——t+1时的预测数;
n——在计算移动平均值时所使用的历史数据的数目,即移动时段的长度。
为了进行预测,需要对每一个t计算出相应的Ft+1,所得到的数据形成一个新的数列,经过两到三次同样的处理,历史数据序列的变化模式将会被揭示出来,这个变化趋势较原始数据的变化幅度小。因此,移动平均法从方法论上属于平滑技术。
2.n的选择
n的选择是移动平均法的难点,不同的n值对所计算的平均数有较大影响。n值越小,表明对近期观测值预测的作用越重视,预测值对数据变化的反应速度也越快,但预测的修匀程度较低,估计值的精度也可能降低;反之,n值越大,预测值的修匀程度越高,但对数据变化的反映程度较慢。
不存在一个确定n值的规则。n一般在3~200之间,视序列长度和预测目标情况而定。一般对水平型数据,n值的选取较为随意;如果历史序列的基本发展趋势变化不大,考虑到较长期观测数据的修匀程度,则n应取大一点;如果重视近期观测数据,例如数据具有趋势性或阶跃性特点,或预测目标的趋势正在不断发生变化,为减少预测误差,则n应取小一点,以使移动平均值更能反映目前的发展变化趋势。
(三)简单移动平均法的特点及应用范围
1.特点
(1)优点。简单易行,容易掌握。
(2)缺点。只是在处理水平型历史数据时才有效,每计算一次移动平均需要最近的n个观测值,而现实中的历史数据远比水平型复杂,所以限制了移动平均法的应用范围。
2.应用范围(www.daowen.com)
一般只适用于以月份或周为单位的短期预测;历史数据最好是水平型的。该法的另外一个用途是对原始数据进行预处理,以消除数据中的异常因素或除去数据中的周期变动成分。
【例3-7】某品牌游戏机某年1、2月各周及3月第一周销售量见表3-9,请用简单移动平均法预测该游戏机3月份的销售量(取n=3)。
【解答】
(1)采用简单移动平均法,n取3:
表3-9 某游戏机专卖店各周销售量
3月第二周销售量: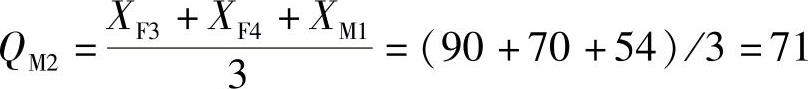 千台
千台
3月第三周销售量: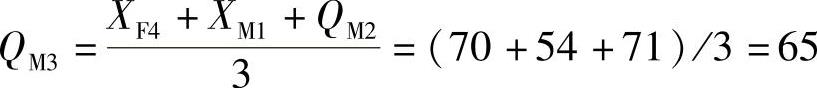 千台
千台
3月第四周销售量: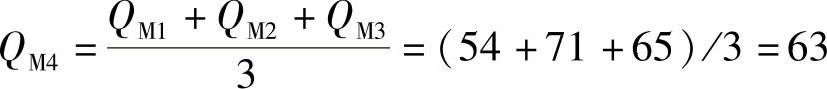 千台
千台
故:3月份的总销售量=XM1+QM2+QM3+QM4=54+71+65+63=253千台
(2)为了使预测更符合当前的发展趋势,可以采用加权移动平均法,即将不同时期的序列给予不同的权重。如对预测的前一期、前二期和前三期分别赋予3、2、1的权重,则:
3月第二周销售量: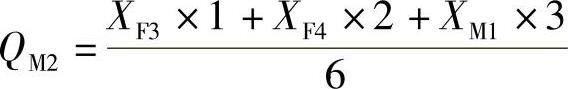
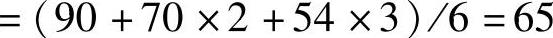 千台
千台
3月第三周销售量: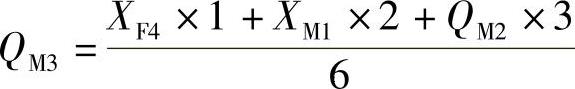
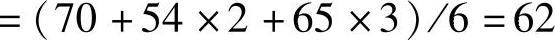 千台
千台
3月第四周销售量: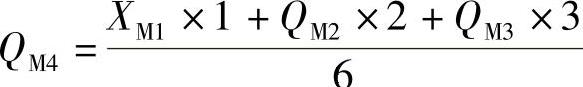
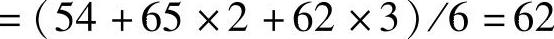 千台
千台
于是,3月份的游戏机总销售量预测为:
XM1+QM2+QM3+QM4=54+65+62+62=243千台
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。








