金融机构通过期限搭配从家庭获取存款，并向非金融机构提供贷款，即通过持有短期负债为长期资产融资。假设在金融危机中，金融机构分为两类：第一类是无须中央银行救助的健康银行，比例为。假设Njt是银行j在t期末的净值，Bjt+1是银行j在t期末从家庭吸收的存款[3]，Sjt是银行对非金融机构的债权，每单位债权的相对价格为Qt。此时，该类银行的资产负债表关系式如下：

假设银行所持有的对非金融机构的债权在t期末的随机收益为Rkt+1。Rt+1与Rkt+1都是内生决定的。在t+1期，第一类银行的净值与其存款和债权之间的关系如下：

其中，Rkt+1-Rt+1可视为银行资产溢价，决定银行总资产QtSjt所获得的高于无风险收益的那部分收益。

假设βiΛt，t+i是银行家在t期所选择的对其t+i期收益的随机折现率。由于银行折现后的资产一定大于其对非金融机构贷款的折现值，因此，银行资产溢价的约束如下：

在无摩擦资本市场中，公式（5.9）为等式约束，即银行资产溢价为零。资本市场存在摩擦时，公式（5.9）大于零，说明在银行获得资金的能力受限制，只能依靠吸收存款融资时，银行资产溢价为正。由于金融机构利用其资产所获得的收益不少于家庭资产可以获得的收益，因此家庭持续将资金存入银行，直到该银行退出该行业。第一类银行家预期期末财富最大化目标函数如下：

为了约束银行从家庭中不断吸纳存款的行为，需要引入道德风险问题。假设期初银行家可以从项目融资中转移比例为λ的资金，将其转入该银行家所属的家庭之中。银行家面临的成本是存款家庭如果发生挤兑会导致金融中介机构破产，并获得银行剩余的1-λ比例的资产，但不能重新获得银行家已经转移的λ比例的资产。

对第一类银行的银行家来说，其激励相容约束为：

即银行家的最终收益应该大于其在期初转移资金的收益，以确保银行的正常经营。

可以用下式重新表达Vjt：(www.daowen.com)

其中，

上式中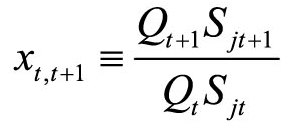，，表示从t期到t+1期的第一类银行资产总增长率。此外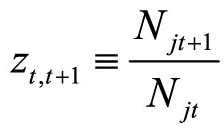，，表示银行净值总增长率。vt表示在银行净值Njt不变的情况下，银行家增加一单位资产QtSjt的预期折现边际收益。ηt表示在银行对非金融机构的债权Sjt不变的情况下，银行家增加一单位银行净值Njt的预期折现边际收益。

当激励相容约束公式（5.11）为等号时，对第一类银行来说，公式（5.12）可转化为如下形式：

其中，φt是金融机构总资产与其净值（或权益）之比，即第一类金融机构的杠杆率。当净值Njt不变时，增大对非金融企业的债权Sjt会导致银行家在期初转移资产的动力增大。因此，公式（5.15）对银行家转移银行资产的动力进行了约束。当Njt＞0时，激励相容约束要求0＜vt＜λ。从公式（5.15）可以看出，vt越大，则银行的杠杆率φt越大，银行向非金融企业放贷的规模Sjt越大，银行家越容易出现道德风险。当vt＞λ时，公式（5.11）永远成立，银行家永远不会出现道德风险。

根据公式（5.8）和公式（5.15），第一类银行净值的递推式可以表示为：

其中，银行净值Njt+1对事后超额回报Rkt+1-Rt+1的敏感度随杠杆率φt增大而增大。根据公式（5.16）可推导出下列关系式：

根据公式（5.15），杠杆率φt与银行个体无关，因此将所有第一类银行加总得到：