套利定价理论认为，证券收益是与某些因素相关的。为此，在介绍套利定价理论之前，必须先了解因素模型（factor models）。我们先前已经涉及了因素模型，这里做进一步讨论。因素模型认为各种证券的收益率均受某个或某几个共同因素影响。各种证券的收益率之所以相关，主要是因为它们都会对这些共同因素起反应。因素模型的主要目的就是找出这些因素并确定证券收益率对这些因素变动的敏感度。

（一）单因素模型

为理解方便，我们循序渐进地从单因素模型开始。单因素模型认为，证券收益率只受一种因素影响。

对于任意的证券i，其在t时期的单因素模型表达式为公式10－15。

其中，rit表示证券i在t时期的收益率；Ft表示该因素在t时期的值；bi表示证券i对该因素的敏感度；εit为证券i的收益率在t时期的随机扰动项，其均值为零，标准差为σit；ai为常数，它表示要素值为0时证券i的预期收益率。因素模型认为，随机扰动项ε与因素是不相关的，且两种证券的随机扰动项之间也是不相关的。

根据上述公式，证券i的预期收益率为公式10－16。

其中，表示该要素的期望值。

根据公式10－15，证券i收益率的方差可以表示为公式10－17。

其中，表示因素F的方差，表示随机变量εi的方差。公式10－17表明，某种证券的风险等于因素风险加上非因素风险

在单因素模型下，证券i和j的收益率的协方差σij如公式10－18所示。

单因素模型可以大大简化马科维茨模型中确定切点处投资组合的过程，因为它只要知道ai、bi、σεi以及和σF即可。

在单因素模型中，证券组合的方差如公式10－19所示。(www.daowen.com)

其中，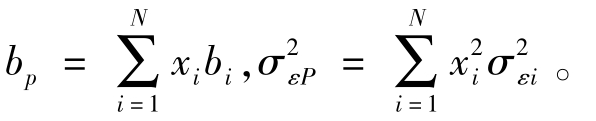

（二）两因素模型

两因素模型认为，证券收益率取决于两个因素，其表达式为公式10－20。

其中，F1t和F2t分别表示影响证券收益率的两个因素在t时期的值，bi1和bi2分别表示证券i对两个因素的敏感度。

在两因素模型中，证券i的预期收益率为公式10－21。

证券i收益率的方差可以表示为公式10－22。

其中，cov（F1，F2）表示两个因素F1和F2之间的协方差。

证券i和证券j的协方差如公式10－23所示。

（三）多因素模型

多因素模型认为，证券i的收益率取决于k个因素，其表达式如公式10－24所示。

应该注意的是，与资本资产定价模型不同，因素模型不是资产定价的均衡模型。在实际运用中，通常可以通过理论分析确定影响证券收益率的各种因素，然后，根据历史数据，运用时间序列法、跨部门法、因素分析法等实证方法估计因素模型。