一、指数、对数的计算

主要知识点

指数的运算法则；对数的运算法则；排列组合的运算法则；诱导公式；特殊角的三角函数值.

重要概念、公式

（2）对数运算法则：

温馨提示：logab·logba ＝________；lg 2＋lg 5 ＝________.

常用对数：lg m＝log10m；自然对数：ln m＝logem（e 是大于1 的无理数）.

（3）排列组合的公式：

（4）特殊角的三角函数值：

二、建立函数模型，应用函数知识解决有关实际问题

主要知识点

用解析法表示函数关系；二次函数的实际应用.

重要概念、公式

（1）面积公式：

三角形的面积是________；矩形的面积是________；梯形的面积是________；平行四边形的面积是________.

（2）利润：

总利润＝总收入________总成本（或总利润＝每件产品的利润×产品的________）；

总收入＝销售每件产品的单价________销售产品的数量.

（1）某矩形的长为x，宽为t＝kx－20，面积为y，则y 与x 的函数关系式是_____________.

（2）某服装店以每件102 元购进一批服装，如果每件以180 元出售，一周可以出售20件，则①每件的利润是________元，总利润是________元；②假设门店每周的固定支出是600元，则该服装店一周的总利润是________元.

（3）二次函数y ＝－2x2＋40x－80 配方得________，所以当x ＝________时，函数有最大值，最大值是　.

【例2】　现修建一个如图所示的“目”字形养鸡场，鸡场的一边靠墙，其中AB，BC，CD 使用甲型材料，EF，GH 使用乙型材料，甲型材料的单价是每米40 元，乙型材料的单价是每米20 元，修建此养鸡场计划花费400 元，设AB 为x 米，养鸡场的面积为y 平方米.

（1）列出y 与x 的函数关系式并求出x 的取值范围；

（2）当AB 长度为多少米时，养鸡场的面积最大？ 并求最大面积.

温馨提示：（1）在求面积问题中，列函数关系时，首先设未知数x，然后需把与面积有关的各线段长用含x 的代数式表示.

（2）采用配方法求最值时，如果函数的右端首项系数不为1，则只能各项提取系数让首项系数变为1，而不能除以系数.

【例3】　某商场以每件30 元的价格购进一种商品，试销中发现这种商品每天的销售量p（件）与每件的售价x（元）满足函数关系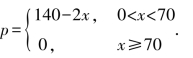

（1）写出商场每天销售这种商品的利润y（元）与售价x 之间的函数关系式（每件商品的利润＝售价－进价）；

（2）商场在销售这种商品的过程中要想获得最大利润，每件商品的售价是多少？ 每天的最大利润是多少？

解：（1）由题意得，当x≥70 时，y ＝0；当0＜x＜70 时，y ＝px ＝（x－30）（140－2x），化简为y ＝－2x2＋200x－4 200，

所以商场每天销售这种商品的利润y（元）与售价x 之间的函数关系式是

（2）由（1）得y ＝－2x2＋200x－4 200 ＝－2（x－50）2＋800，0＜x＜70.

所以当这种商品每件的售价为50 元时，商场获得的利润最大，其每天的最大销售利润是800 元.

1.某种砌墙的建筑材料总长是24 米，如果用此建筑材料修建一个矩形花台，如图所示.在矩形花台中，设AB 为x 米，矩形的面积为y 平方米.

（1）写出矩形花台的面积y 与AB 的长度x 的函数关系式，并写出x 的取值范围；

（2）当矩形花台的面积不少于20 平方米时，求x 的取值范围；

（3）当AB 是多少米时矩形花台的面积最大？ 最大面积是多少？

（1）写出围成的梯形面积S 与x 的函数关系式，并求出x的定义域；（2）当x 取何值时，此建筑围成的梯形面积最大？ 最大面积是多少？

3.在矩形ABCD 中，AB ＝10 m，BC ＝8 m，E，F，G，H 分别为AB，BC，CD，DA 边上的点，且AE ＝AH ＝CF ＝CG，设AE ＝x米，四边形EFGH 的面积为y 平方米.

（1）写出四边形EFGH 的面积y 与AE 的长度x 的函数关系式；

（2）当x 取何值时，四边形EFGH 的面积最大？ 并求出最大面积.

4.如图所示，在△ABC 中，C ＝90°，AC ＝30 cm，BC ＝20 cm，点M 由C 向B 方向以每秒1 厘米的速度移动，同时点N 由A 向C方向以每秒2 厘米的速度移动.

（1）设M，N 的运动时间是x 秒，写出四边形ABMN 的面积y与x 的函数关系式，并求x 的取值范围；

（2）当运动时间为多少秒时，四边形ABMN 的面积最小？ 最小面积是多少？

5.某种产品每件售价为60 元，每月可以售出300 件，经市场调查发现，每涨价1 元每月少售出10 件，每降价1 元每月多售出20 件，这种产品的进价为每件40 元，如何定价才能使所获利润最大？

6.已知某种商品，平均每月销量x 件与货价p（元／件）之间的函数关系为p ＝120－x，销售x 件商品的成本函数为c＝500＋30x.

（1）写出每月利润y（元）与x（件）的函数关系式；

（2）当x 为何值时，利润y 最大？ 并求出最大利润.

7.某产品的成本是10 元，在试销阶段，每件产品的销售价x 元与日销售量P 之间的关系如表所示，销售量P 是销售价x 的一次函数.

（1）求P 与x 的函数关系式；

（2）设y 表示每日销售此产品的利润，写出y 与x 的函数关系式.售价为多少元时，每日的利润最大？ 最大利润是多少？(www.daowen.com)

8.新世纪超市以每盒42 元的价钱购进一种巧克力，根据试销得知：这种巧克力每天的销售量t（盒）与每盒的销售价x（元／盒）可以看成是一次函数关系：t＝－3x＋204.

（1）写出新世纪超市每天卖这种巧克力的销售利润y（元）与每盒的销售价x 之间的函数关系式（每天的销售利润是指所卖出巧克力的销售价与购进价的差）；

（2）如果新世纪超市想每天获得最大的销售利润，那么每盒的销售价定为多少时，可以实现？ 最大销售利润是多少？

9.某件商品的进价为40 元，售价为50 元，每个月可卖出210 件，如果商品的售价每上涨1 元，则每个月少卖10 件（每件不高于65 元）.设每件商品的售价上涨x 元（x 为整数），每个月的销售利润为y 元.

（1）求y 与x 的函数关系式，并直接写出自变量x 的取值范围；

（2）若每个月的利润为2 200 元，每件商品的售价应定为多少元；

（3）每件商品的售价定为多少元时，每个月可获得最大利润？ 最大利润是多少元？

10.某食品加工厂生产A 种食品，每件销售价是30 元，招收一名新工人每天生产食品为P 件，设这名新工人第x 天生产的食品数量P（件）与x 的函数关系是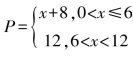，且每件食品的成本Q（元）与x 的函数关系是Q＝0.5x＋24.

（1）设这名新工人第x 天创造的利润为w 元，写出w 与x 的函数关系式；

（2）求这名新工人第几天创造的利润最大？ 最大利润是多少元？

三、待定系数法

主要知识点

指数函数、对数函数、二次函数的解析表达式；函数的图像和性质；指数、对数的简单计算.

重要概念、公式

（1）二次函数的解析式是________________，其顶点式是________________，其单调性：

当a＞0 时，函数在区间________________上为增函数，在区间________________上为减函数；

当a＜0 时，函数在区间________________上为增函数，在区间________________上为减函数.

（2）指数函数的解析式是________________，图像必过点________，其单调性：

当0＜a＜1 时，函数在区间（－∞，＋∞）上为________函数；

当a＞1 时，函数在区间（－∞，＋∞）上为________函数.

（3）对数函数的解析式是________________，图像必过点________，其单调性：

当0＜a＜1 时，函数在区间（0，＋∞）上为________函数；

当a＞1 时，函数在区间（0，＋∞）上为________函数.

（1）求a 的值；

（2）若f（x＋2）＜f（x2），求x 的取值范围.

【例5】　已知函数f（x）＝k－log6（x2－3x－4），且f（－2）＝2.

（1）求k 的值；

（2）求函数f（x）的定义域；

（3）若f（x）≥2，求x 的取值范围.解：（1）因为f（－2）＝2，所以k－log6［（－2）2－3×（－2）－4］＝2，

则k ＝log66＋2 ＝1＋2 ＝3，所以k ＝3.

（2）要使函数f（x）有意义，必须满足

x2－3x－4＞0

（x－4）（x＋1）＞0

x＜－1 或x＞4，

所以函数f（x）的定义域是｛x x＜－1 或x＞4｝.

（3）由（1）得f（x）＝3－log6（x2－3x－4），

因为f（x）≥2，所以

3－log6（x2－3x－4）≥2

log6（x2－3x－4）≤1

x2－3x－4≤6

x2－3x－10≤0

（x－5）（x＋2）≤0，

温馨提示：指数不等式的解法是两边化成同底的指数，对数不等式的解法是两边化成同底的对数，再根据指（对）数函数的单调性转化成一元一次或一元二次不等式，再求解集.

1.已知二次函数f（x）的顶点坐标为（2，3），且它的图像经过A（1，2），（1）求f（x）的解析表达式；（2）若f（x）≥0，求x 的取值范围.

2.已知函数f（x）＝ax－2（a＞0 且a≠1）的图像经过点P（1，1），（1）求f（3）；（2）当x 取何值时，f（x）＞7？

3.已知f（x）＝log2（x2－2x），（1）求函数f（x）的定义域；（2）当x 为何值时，f（x）≤3？

4.已知二次函数f（x）的图像经过3 点A（－3，0），B（1，0），C（－4，5），（1）求f（x）的解析表达式；（2）求函数f（x）的单调区间和函数的值域；（3）当x 为何值时，f（x）＞0？

5.已知指数函数f（x）的图像经过点（－1，3），（1）求f（x）的解析表达式；（2）若1－f（2xx2）＞0，求x 的取值范围.

7.已知函数y1 ＝x2－2x＋5 的图像交y 轴于点A，它的对称轴为直线l，函数y2 ＝ax（a＞1）的图像交y 轴于点B，交直线l 于点C，（1）求△ABC 的面积；（2）设a ＝3，求AC 的长.