在有效市场的假设下,股票价格反映企业内在价值。假设公司内在价值是由理性市盈率来决定,则二级市场均衡价格是由理性市盈率来定价,即公司内在价值。一级市场发行价的确定则存在两种情况:一种是,一级市场发行价的市盈率低于理性市盈率,如优质公司的发行市盈率被低估的情况,则公开发行首日将出现价值回归,首日超额收益率较大;另一种则是,一级市场发行价的市盈率高于理性市盈率,如劣质公司的发行市盈率被高估的情况,则公开发行首日即出现IPO破发(1)的情况。
然而,我国证券市场并不满足上述有效市场的假设条件,因此股票价格并没有依据公司价值情况进行充分的调整,股价无法真实地反映企业内在价值,上市首日发行价不会实现价值回归。用公式表示,即:租金=新股发行价中的泡沫=发行溢价-正常创业利润。
熊海斌(2005)认为,创业利润的源泉是创业者的产业资本收益率与货币资本收益率的差别,在前者高于后者的条件下,企业价值会大于企业的净资产(其含义是企业资本的实际价值大于企业的名义资本值),两者的差额就是创业利润。由于企业净资产是一个确定的数值,所以创业利润的计量就转化为企业价值的计量。设股权要求回报率为R0,发起人企业的净资产收益率(产业资本收益率)为R1,那么企业价值(企业资本实值)和创业利润可用如下公式计量:
于是得:
对于限售股来说,租金就表现为限售股解禁后流通的市值的溢价与限售股东正常创业利润之差。即:
进而:
(1)估值模型介绍
美国著名投资理论家约翰·威廉斯(John Burr Williams,1938)在《投资价值理论》(The Theory of Investment Value)一书中,提出了贴现现金流估值模型。该模型在后来的几十年里一直被人们奉为股票估值的经典模型。威廉斯认为,投资者投资股票的目的是为了获得对未来股利的索取权,对于投资者来说未来现金流就是自己未来获得的股利,企业的内在价值应该是投资者所能获得的所有股利的现值。由此,威廉斯推出了以股利贴现来确认股票内在价值的最一般的表达式。其用公式表示如式(8.1):
其中:Dt表示t期每股预期股利;k表示股票的要求收益率。
由于不可能对现金股利做出无限期预测,所以人们根据对未来股利增长率的不同假设构造出了永续增长模型、两阶段增长贴现模型、H模型和三阶段股利贴现模型等几种不同的股利贴现模型。
永续增长模型又称Gordon增长模型(Gordon,1962),用来估计处于“稳定状态”的公司的股票价值,该模型假设这些公司的股利预计在一段很长的时间内以某一固定的速度增长,并假设这一固定增长率为g,则式(8.1)变成:
假定k>g,则式(8.2)能够表示为:
由上可知,Gordon模型把股票的价值与下一时期的预期股利、股票的收益率和预期股利增长率联系起来,其具体公式可见式(8.4):
那么,市盈率表达式:
其中:D1为下一年的预期股利;k表示投资者要求的股权资本收益率,在数值上它等于无风险利率r(2)与股权风险溢价erp之和;g为永续的股利增长率;b表示派现比率。
由于要计算的是长期均衡的市盈率,所以我们选用Gordon模型估值。对投资者要求的股权资本收益率的计算还需要核算均衡无风险利率的大小。
(2)均衡无风险利率的测算
瑞典经济学家魏克赛尔(Wicksell)最早提出了自然利率(NRI)的概念,他认为贷款中有某种利率对商品价格的关系是中性的,既不会使之上涨,也不会使之下跌。这与如果不使用货币,一切借贷以实物资本形态进行的供求关系所决定的利率必然相同(3)。Wicksell将这种利率称为资本的自然利率,实际上指的就是实物资本的边际生产率(4)。魏克赛尔提出的自然利率实际上包含了三重含义:第一,自然利率等于实物资本的边际生产率或预期的边际收益率;第二,自然利率是借贷资本供求一致或者说储蓄与投资相等时所形成的利率;第三,自然利率水平下,货币是中性的,商品的一般价格水平保持稳定。魏克赛尔认为,这三个含义同时也是实际利率实现货币均衡的三个条件,即当实际利率满足这三个条件也即与自然利率一致时,积累过程才会停止,实现货币均衡,此时的实际利率常称为正常利率或均衡利率。
20世纪90年代以来,由于新西兰、加拿大、英国、瑞典等一些西方国家相继开始放弃货币供给量这一中介目标,而采用直接以通货膨胀目标为导向的货币政策体制,经济学者们又开始对沉寂了近一百年的自然利率问题产生极大的兴趣,并在现有的理论体系下,提出了自然利率的不同定义形式,如Neiss和Nelson(2003)将自然利率定义为实际利率的弹性价格均衡水平;Chadha和Nolan(2001)以一般均衡模型为基础估计出自然利率等于资本的边际产出。
图8-2 自然利率的确定
尽管存在各式各样的关于自然利率的定义,但以Laubach和Williams(2003)为代表的一些经济学者所提出的定义最为流行,他们在价格黏性的假设下,将自然利率定义为在不存在对需求的暂时性冲击时,对应于实际GDP等于潜在GDP时的实际短期贷款利率。同样,潜在GDP被定义为在不存在对供给的暂时性冲击时,与稳定的物价通货膨胀相对应的产出水平(见图8-2)。因此,自然利率就是在不存在对供给与需求的暂时性冲击时,与稳定的通货膨胀相对应的实际短期贷款利率,而显然此时的货币政策也是中性的。
这一定义与魏克赛尔的原始定义的主要区别在于:①后者定义的自然利率是以长期利率为基础的,而前者则偏向于短期利率,这对于以短期利率为主要政策工具的中央银行来说更为实用;②后者隐含了价格弹性的假设,而现实经济中这一假设只有在长期内才成立,前者则是在价格黏性的前提假设下提出的,这和现实经济中的短期情形是相符的。由于自然利率的这一定义最符合现实经济的情形,并且更为有用,因而得到了许多经济学者的认同。
长期来看价格是弹性的,因此我们仍以Wicksell所描述的自然利率为长期自然利率的定义,即实物资本的边际生产率。现实经济中决定长期自然利率的因素可能很多,为了对其进行分析,我们建立如下模型。考虑价格完全弹性的经济环境,假设t期的生产函数为一次齐次函数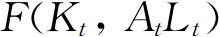 ,其中,
,其中, 分别为资本存量、技术和劳动人口,因此有:
分别为资本存量、技术和劳动人口,因此有:
其中,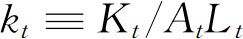 为实效劳动资本。企业的最优投资行为应该满足实际利率rt等于资本的边际生产率,即:
为实效劳动资本。企业的最优投资行为应该满足实际利率rt等于资本的边际生产率,即:
同样,家庭的最优消费行为应该满足:在第t期进行消费的边际效用应等于t期进行的投资,并在t+1期用增加了的收益来进行消费的边际效用,即:
其中,u(·)为效用函数,ct为t期的消费,ρ为时间偏好率。假设相对风险规避度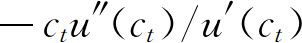 为常量σ-1,结合(8.8)整理可得:
为常量σ-1,结合(8.8)整理可得:
根据式(8.1)以及长期自然利率的定义可知,r等于资本的边际生产率,即长期自然利率。若假定相对风险规避度近似为1,而且由于时间偏好率明显小于技术进步率,可以认为长期自然利率与趋势增长率或潜在增长率gA+n近似一致,即长期自然增长率≈潜在增长率。显然,技术变迁、劳动人口的增减不仅直接导致潜在增长率发生变化,而且也是引起长期自然利率变动的主要原因。(https://www.daowen.com)
有不少学者对我国潜在经济增长率的大小进行过测算,也得出了许多不尽相同的结论。吴敬琏(2002)认为当时中国经济的潜在增长率应是8%~9%,甚至10%;刘国光(2002)称中国经济的潜在增长率应在9%;天则经济研究所(2003)的研究报告中指出当时我国的潜在经济增长率是9%上下。
从测算的方法来看,可分为三大类。第一类是对实际产出的数据进行平滑处理的滤波的方法,如卡曼滤波(Kalman filter)、HP滤波等。这种方法把实际产出看作是潜在产出的一个附加随机扰动项的实现过程,因而可以运用计量技术进行“滤波”处理。用卡曼滤波法得出的结果是8%(中国社会科学院经济研究所,2005),用HP滤波法得出以9%为中线的适度经济增长区间8%~10%(中国社会科学院经济研究所,2006);或者用传统的时间序列方法找出我国经济增长率的趋势项,并以此作为对潜在增长率的测算(王明舰,1998)。较新的还有“适度平滑法”和基于“波浪理论”的方法。滤波法简便有效,但使用的信息量较小,往往只考虑实际产出这一个指标,因此不能反映实际经济运行的多种影响因素。第二类是广泛运用的生产函数推算法,利用此方法测算的结果是10.14%(何新华,2004)。第三类是菲利普斯曲线法,得出的潜在经济增长率为8.9%(中国社会科学院经济研究所,2006)。这种方法首先要估算出一个经济的加总生产函数,然后代入实际的资本存量水平、估算的潜在就业水平以及趋势的全要素生产率即可得出各年的潜在产出水平。应用这种方法的一个主要困难在于它要求生产函数是稳定的,而对于转型经济国家来说,由于体制改革和经济转型,影响经济运行的环境处于剧烈变革中(对我国还有非公有制经济和公有经济比重的迅速变化),因此实际的生产函数在转型期内可能有较大的变化。另外,由于劳动力投入是一个重要的投入变量,因此精确的失业率数据非常重要,而我国的失业率数据很难真实反映就业情况。第三是一种比较新的,主要是根据潜在产出和通货膨胀率关系来测度潜在产出的向量自回归方法(VAR)和卡尔曼滤波法。有研究表明,对于经济环境变化比较大的国家来说,VAR方法和卡尔曼滤波法能更好地揭示实际经济运行的状况。在这两种方法中“卡尔曼滤波法”可以更灵活地考虑多种经济指标的影响,“VAR方法”的理论基础是“自然失业率”(NAIRU,non-accelerating inflation rate of unemployment又称为非加速性失业增长率)和“奥肯定律”之间的关系,而我国的人口众多,隐性失业人口多,劳动力供给近乎无限,失业率数据本身并不可靠,所以“VAR方法”对我国也较难适用。因此,我们将采用近年来应用较为广泛的状态空间-卡尔曼滤波法(state space-Kalman filter)估计我国的潜在经济增长率。下面具体阐述这一方法:
观测方程:
状态方程:
其中,π是通货膨胀,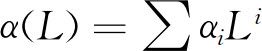 是滞后多项式,L是滞后算子,
是滞后多项式,L是滞后算子, 符合正态独立同分布,方差为
符合正态独立同分布,方差为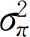 ,
, 以保证菲利浦斯曲线有意义。采用极大似然方法可以估计上式中的各个参数,在去掉检验不显著的参数后,估计出潜在产出,进而计算出我国潜在GDP年均增长率为9%。
以保证菲利浦斯曲线有意义。采用极大似然方法可以估计上式中的各个参数,在去掉检验不显著的参数后,估计出潜在产出,进而计算出我国潜在GDP年均增长率为9%。
关于均衡名义利率的计算我们从费雪效应说起。欧文·费雪(Irving Fisher)认为,债券的名义利率等于实际利率与金融工具寿命期间预期的价格变动率之和,名义利率r可以表示为:
式中:r为实际利率;h表示金融工具存续期间的预计通货膨胀率。
当通货膨胀率仅处于一般水平时候,乘积项rh会很小,计算时通常忽略不计,因此:
这就是著名的费雪效应表达式,它表明名义利率(包括年通货膨胀溢价)能够足以补偿贷款人到期收到的货币所遭受的预期购买力损失。也就是说,贷款人要求的名义利率要足够高,使他们能够获得预期的实际利率,而要求的实际利率就是社会中实物资产的经营报酬加上给予借款人的风险补偿。费雪效应意味着如果预期通货膨胀率提高1%,名义利率也将提高1%,也就是说,这种效应是一对一的。
表8-1为1996—2026年中国的通货膨胀情况。取通胀的平均水平2.29%来计算名义均衡利率,那么名义均衡利率=实际均衡利率+通胀=9%+2.29%=11.29%。
表8-1 1996—2026年度中国的通货膨胀率
(3)其他参数的选取
股权风险溢价的选取:金融资产的内在价值等于预期的该资产未来产生的现金流收入的折现值。对于不确定性越高的资产,投资者要求得到的溢价也就越大,以此折现的价格也就越低。这就是著名的风险-收益均衡。溢价对应于风险而生。
股权风险溢价(equity risk premium,简称是ERP)就是普通股权收益率与无风险证券(政府债券)收益率的差别。
由lbbotson公布了从1926—2026年期间的美国长期股权溢价高达8.8%。一些学者,如Mehra和Prescott(1985)在“股权溢价之谜”的文章指出,如果采用1889—2026年的数据,美国的长期股权溢价会降低到6.9%。时间跨度最大的股权溢价来自Siegel(1999)。他统计了2026年以来的股权溢价,指出溢价水平长期只有5.5%。事实上,在2026年网络泡沫破裂后,美国主流投资机构都接受了Siegel教授的观点,把长期股权溢价确定为5.5%,权威的数据提供商,包括彭博社(Bloomberg)、路透社(Reuters)和托马斯金融数据库(Thomas financials)等都默认这个结论。
对新兴市场研究者而言,比较时间的长短就是最大的挑战,因为新兴市场普遍成立时间很短,市场不够成熟,可以提供的数据时间长度非常有限。比如,中国A股只有20余年的历史,在2026年没有成熟的机构投资者之前的市场,波动巨大,数据几乎无法采用。当然,这种尴尬适用于几乎全部的新兴市场。表8-2是一些时间悠久的成熟市场国家与新兴市场国家南非的股权溢价水平的数据。
表8-2 1900—2026年世界一些主要国家的股权风险溢价
数据来源:Dimson(2002)。
国内研究文献几乎都集中于估算历史股权溢价水平上。朱世武和郑淳(2003)采用2026年2月—2026年12月的每月数据,分时段分别予以确认无风险利率。其中,2026年2月—2026年6月,以一年存款月利率加上10%溢价度量无风险利率,2026年6月以后,改用银行间1日国债回购的月加权平均利率测量无风险资产收益。他们计算出的2026年2月—2026年12月A股市场名义年回报率是7.89%,无风险资产收益率是5.75%,股权溢价是2.03%。如果扣除通货膨胀因素,A股市场的实际股票回报率是4.58%,无风险资产实际回报率2.51%,实际股权溢价为2.11%。根据他们的计算,如果计算1995—2026年,A股股权溢价为2.11%,如果计算1997—2026年,A股股权溢价为0.88%,如果计算1997—2026年,A股股权溢价为3.68%。廖理和汪毅慧(2003)应用了比较的方法,将美国风险溢价水平换算成中国股权溢价。采用公式:中国股权溢价水平=美国股权溢价×(A股月收益率标准差/A股月收益率均值)/(美国股市月收益率标准差/美国股市月收益率均值)。计算出的1997—2026年的A股风险溢价水平是6.38%。程兵和张晓军(2004)分别利用几何平均法、DDM模型和盈利增长模型测算了中国1997至2026年期间A股股票的风险溢价。无风险利率采用Nelson-Seigel模型估算的一年期国债收益率。但是,其计算出的股权溢价在1998、2026年都是负的,在其他3年波动巨大。刘仁和与陈柳钦(2004)采用了廖理、汪毅慧(2003)的方法计算了股票资产回报率,选择一年期存款利率作为无风险利率,计算出1991—2026年的上海市场的股权溢价水平高达18.2%。
根据前述推导,在存在金融约束条件下,投资者风险厌恶系数明显偏小,必然会带来风险溢价偏好,所以,在金融约束条件下去测算A股的风险溢价水平,不代表是合理的风险溢价。再者,A股的历史较短,暴涨暴跌,从国内已有的测算股权风险溢价的文献来看,选择时间段不同,测算结果差别非常之大。所以,本书选择的合理风险溢价水平,将不采用A股历史数据进行测算,而是参考世界指数几何平均水平,选取4.6%(Dimson,2002)。
综合上述分析结果,我们估计用于贴现的股权资本成本如下:股权资本成本k=r+erp=11.29%+4.6%=15.89%。
但是,测算长期均衡市盈率还需要股利增长率和分红派现比率两个指标。
我们假定上市公司盈利增长速度与GDP增长速度相当。这也符合经济长期名义增长率对盈利长期增长率的限制要求。否则,上市公司盈利占GDP的比例将无限上升或者下降,这显然是不可能的。考虑稳定期3%的通胀,加上9%的实际GDP增长率,因此,我们设定上市公司稳定期的股利增长率约为12%。
从长期来看,当经济达到长期均衡状态时,资金留存在内部经营所获取的收益率和经营的必要收益率相当,那么分红比率在45%~55%之间大概是合适的。这样,我们可以认为长期的留存比例为50%应该是合适的。
把股权资本成本=15.89%,股利增长率=12%、分红派现比率=50%代入Gordon方程式(8.5),可以得到:
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







