利率政策对证券价格的间接影响是指利率政策的变化影响实质经济增长,亦即影响证券市场的“基本面”,从而改变投资者对经济的未来预期,通过投资者的心理变化、市场行为来对股票价格形成影响。下面我们从利率政策对投资者的风险偏好的影响来阐述这种影响机制。
这里所谓的架构(frame)是指一个决策的类型。传统金融理论假定架构独立(frame independence)或者说架构是透明的,即风险与收益都是透明的、客观的,投资者可以通过透明客观的风险、收益观测到全部决策过程。米勒(Merton Miller)曾形象地解释架构独立的概念,他说:如果你将一块钱从右边的口袋转到左边的口袋,你并不因此而更富有。行为金融学则认为,许多架构不是透明的,相反,是相当晦暗的。当一个人难以看到整个晦暗的架构时,他的决策要依赖于他所使用的具体架构。结果,形式上的不同就会有实质的不同,行为反映了架构依赖(Shefrin,2003)。Kanheman和Tversky(1979)设计了一个心理学实验(4),研究人们对预期亏损的反应,提供了架构依赖的证据。他们把这种现象叫做亏损回避。从上述实验可以看出,人们喜欢一种使亏损变得模糊的架构。让人们感觉到对导致亏损的决策负有责任时,人们对亏损的经历感受就更强烈。尽管迄今为止股市制度仍存在很多不完善之处,但股价的波动不定也给人们提供了盈利的机会,而且这种机会在牛市阶段还是很显著的,而相对于银行存款微不足道的利息,这种机会使人产生憧憬和想象。正如人们所说的,股市可以让人一夜暴富,也可以让人瞬间倾家荡产,这因为这样,股市才成为一个令人向往的地方,许多股民才会在股海的沉浮中乐此不疲。架构依赖理论表明,在管制下的低利率状态下,投资者的风险偏好将会大大上升。
依据行为金融学的框架依赖理论,负利率将会推高投资者的风险偏好。本节将从资产定价模型角度阐述这一问题,对所有投资者来说,投资的目的是最大化效用,考虑离散效用函数的形式,当期之后的每期效用以β为贴现率,最大化的效用就是各期效用贴现和的数学期望最大化,即: ,其中,β是贴现率,也称时间偏好因子,Ct+j是消费者在第t+j期的消费额,U(·)是消费的即期效用函数。假定投资者能够对资产i进行自由交易,并且可以在时间t到t+1之间获得该资产的一个总体回报率(1+
,其中,β是贴现率,也称时间偏好因子,Ct+j是消费者在第t+j期的消费额,U(·)是消费的即期效用函数。假定投资者能够对资产i进行自由交易,并且可以在时间t到t+1之间获得该资产的一个总体回报率(1+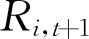 )。并且假定该投资者在时间t的消费额为Ct,我们可以用一阶最优的欧拉方程来表述消费者的最优消费和投资计划:
)。并且假定该投资者在时间t的消费额为Ct,我们可以用一阶最优的欧拉方程来表述消费者的最优消费和投资计划:
(5.2)式左边是减少当期一元钱的消费所产生的边际效用成本,等号右边是将这一元投资在资产i,并在下期消费所产生的边际效用收益的贴现的期望。最优化的消费和投资选择就是要使边际效用成本和边际效用收益相等的选择。
因为在t期,U′(Ct)可以当作一个已知量,而非随机量,将(5.2)式两边同时除以U′(Ct),我们可以得到:
其中定义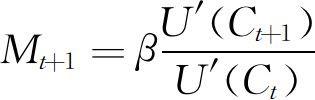 ,被称为是随机贴现因子(stochastic discount factor),Mt+1也经常被称为边际替代率(marginal rate of substitution),在该等式中,Mt+1是投资者愿意在时间t+1消费替代在时间t消费的比率。
,被称为是随机贴现因子(stochastic discount factor),Mt+1也经常被称为边际替代率(marginal rate of substitution),在该等式中,Mt+1是投资者愿意在时间t+1消费替代在时间t消费的比率。
式(5.4)的意义在于,资产回报率的数据尽管在横截面层面和时间序列层面上都很不同,可是使用随机贴现因子贴现后的资产回报率,其数学期望都是等于1的,因此式(5.4)适用于各种各样的资产定价公式,可以涵盖股票、债权和期权等,使我们可以以一种理论来解释所有资产定价问题。
根据数学期望的性质,乘积的数学期望等于数学期望的乘积加上协方差,有
整理,得:
对于任何资产,只要其在时间t到时间t+1的总回报率等于(1+Ri,t+1),就会满足等式(5.6)。对于无风险资产也是满足的。无风险收益的资产其回报在理论上可以看成是个非随机的量,与随机贴现因子的协方差为零,所以对于无风险资产,有
注意到随机贴现因子Mt+1与资产的种类并无关系,因此对于任何资产i均适用,将(5.7)式代入(5.6)式中,有:
按照Hansen和Singleton(1983)的假设,资产回报和随机贴现因子的联合分布具有对数正态性和同方差性。尽管这些假设基本上是不现实的,因为股票回报的分布存在厚尾现象,而其方差也随着时间的变化而变化,但这些假设有利于分析股权溢价,可以较好地把握其主要决定因素。
对于一个服从对数正态分布的随机变量X来说,Y=lnX服从正态分布,Y服从N(u,σ2)。令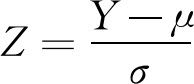 ,再根据标准正态分布随机变量的矩母函数的性质,有
,再根据标准正态分布随机变量的矩母函数的性质,有
利用资产回报和随机贴现因子的联合条件对数正态分布和同方差性,我们对(5.4)式的两端取自然对数,得:
其中,我们令 ,
,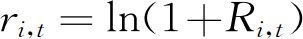 ,
,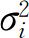 是对数回报的无条件方差,
是对数回报的无条件方差,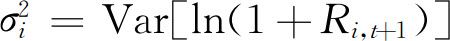 ,
,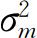 是随机贴现因子对数的无条件方差,
是随机贴现因子对数的无条件方差, ,
,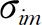 定义为无条件协方差,即
定义为无条件协方差,即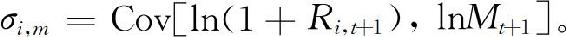 。(https://www.daowen.com)
。(https://www.daowen.com)
对于无风险资产,其方差和其与随机贴现因子的协方差均为零,所以无风险资产服从:
可以看出,(5.14)式是(5.7)式的自然对数形式。
结合(5.13)和(5.14)式,可以推出:
在消费资本资产定价模型中,消费者的行为特征是通过效用函数来刻画的。Mehra和Prescott(1985)假设存在一个具有离散时间幂效用函数最大化的代表性行为者,该行为者的效用函数建立在其消费Ci之上:
式(5.16)中,α是相对风险厌恶系数。在资本市场上我们总是假定投资者是风险厌恶类型的。我们定义绝对风险厌恶(absolute risk averision,ARA), ,它衡量的是在既定消费水平下的风险厌恶程度。我们将计量绝对风险厌恶的表达式乘以消费水平,从而得到相对风险厌恶RRA(relative risk aversion)的表达式,
,它衡量的是在既定消费水平下的风险厌恶程度。我们将计量绝对风险厌恶的表达式乘以消费水平,从而得到相对风险厌恶RRA(relative risk aversion)的表达式,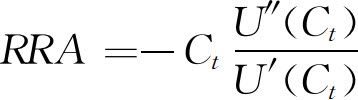 。
。
对于(5.16)式,我们可以计算出其RRA=α,当α→1时,(5.16)式趋向于ln(Ct)。
幂效用函数的假设意味着消费的边际效用为 ,那么随机贴现因子
,那么随机贴现因子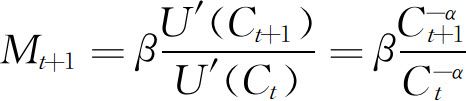 ,随机贴现因子是对数正态的假设意味着消费也是对数正态的。
,随机贴现因子是对数正态的假设意味着消费也是对数正态的。
由
 。其中,
。其中,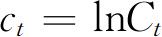 。
。
那么(5.13)式可变为
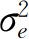 为对数消费的无条件方差,σie为无条件协方差。
为对数消费的无条件方差,σie为无条件协方差。
等式(5.14)变为
等式(5.15)变为
从式(5.19)可以看出,任何资产的对数股权溢价等于相对风险回避系数乘以该资产回报和消费增长的协方差。直观上理解,α越小,则投资者的风险偏好越大,所要求的风险补偿也就越小,该项资产的价格也就越高。
上一节架构依赖理论告诉我们,低利率的金融约束政策将会导致投资者出现较高的风险偏好,这一节则告诉我们,投资者的风险偏好越大,风险厌恶系数α越小,那么资产的价格将会越高,放在一起解读,就是低利率的金融约束政策通过放大投资者的风险偏好间接产生了股市的泡沫。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。








