可对方程两边取对数

令y′c=lgyc，A=lga，B=lgb，则得一元线性模型

又如，模型是高次方程

只要令x1=x，x2=x2，x3=x3，…，就可转化为多元线性模型

现举12个同类企业的月产量和单位产品成本的资料，说明其研究方法，见表7-9所示。

表7-9　12个同类企业月产量和单位产品成本

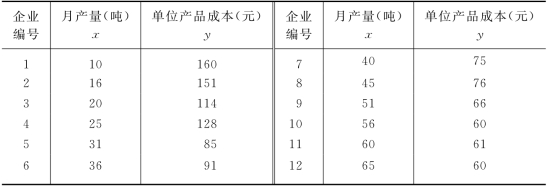
从表7-9资料中可以看出在月产量与单位产品成本之间存在着一定的依存关系，因为随着产量的逐渐增多，单位产品成本有随之而逐渐降低的趋势。但单位产品成本的降低程度并不是随着产量的增加而均等地变化。例如，把x与y两个数列加以比较，在开始阶段，x值每增加一个单位时，y值降低得很多，随后x值继续增加，y值虽也有降低，但和开始阶段比较，其降低程度逐渐下降。这种情形从图7-6中看得比较明显。

从图7-6中观察点的分布来看，适用于配合指数曲线回归方程yc=abx（b＞0）

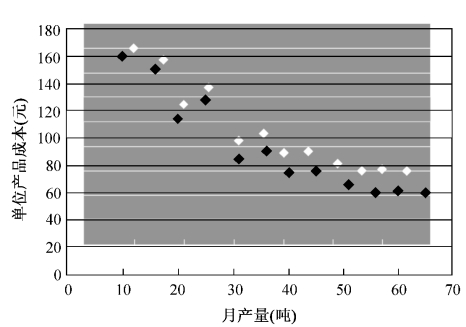
图7-6　曲线散点图

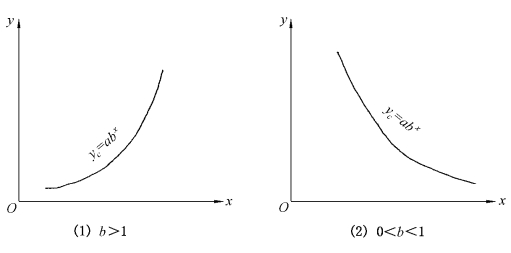
式中有两个待定参数a、b，自变量x是参数b的指数。当b＞1，为递增曲线；当0＜b＜1，为递减曲线。如图7-7所示。

(www.daowen.com)

图7-7　递增与递减曲线

现仍以yc代表估计值，则回归方程就是

将公式的两端取对数，得

如令y′c=lgyc，A=lga，B=lgb

则上述指数方程变为

可见经过代换之后转化成为直线关系方程的形式，这就可以按照前面求直线回归方程中参数的方法以求得a，b。根据最小平方原理，上式中的A和B应满足下列方程组

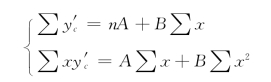
解上式，可以得A及B，再根据A=lga，B=lgb的关系式，便可以求出a、b的值。现在根据表7-9资料进行计算，结果如表7-10所示。

表7-10　12个同类企业的月产量与单位产品成本曲线回归计算表

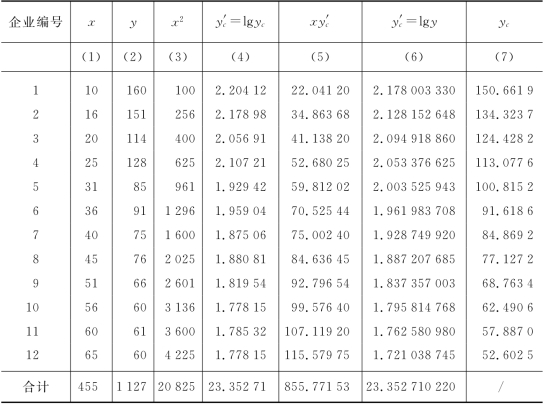
现在分别求得A及B的反对数，由A=lga，B=lgb

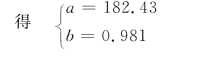
于是指数曲线回归方程为