在实际中,客观现象之间的联系是复杂的,通常影响因变量的因素不止一个。在统计中,研究一个因变量和多个自变量的回归分析就是多元回分分析。多元回归可分为多元线性回归和多元非线性回归。这里只讨论最一般的多元线性回归。
多元线性回归分析的步骤、方法和一元线性回归分析基本上是相同的,不过在计算上比较复杂些。
(一)多元线性回归方程
为了便于理解,我们先介绍二元线性回归方程,即以一个因变量y与两个自变量x1和x2线性回归,其方程式为
![]()
式中,yc——因变量估计值;
a,b1,b2——为三个参数。
确定a,b1,b2的数值,也要用最小平方法,使∑(y-yc)2为最小值。因为式中有三个参数,从而要确定如下的三个规范方程式

例如,某地区玻璃销售额与该地区汽车制造业和建筑业的生产关系相当密切,现有表7-8资料,预测第18年玻璃的销售额。
表7-8 某地区玻璃销售量与汽车产量、建筑业产值资料

续表

根据表7-8资料计算得

代入求解参数的联立方程组

解得
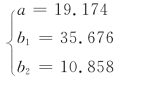 (https://www.daowen.com)
(https://www.daowen.com)
所以方程yc=19.174+35.676x1+10.858x2
如第18年汽车产值为7.42万辆,建筑业产值为50.28千万元。
则预测该年玻璃销售额

把上面的方法推广到多个自变量,设因变量y受n个自变量x1,x2,x3,…,xn的影响,其回归方程式为
![]()
式中,a,bi(i=1,2,3,…,n)为参数,根据最小平方法的原理,使∑(y-yc)2为最小值。因为有n+1个参数,应确定n+1个方程式
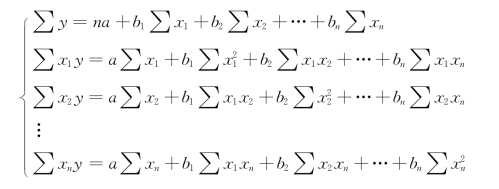
(二)多元线性回归模型的判定系数和估计标准误差
同一元线性回归方程一样,对已确定的二元线性回归方程,可以从判定系数和估计标准误差两方面来测定它的拟合度。
1.判定系数r2

简捷公式为:
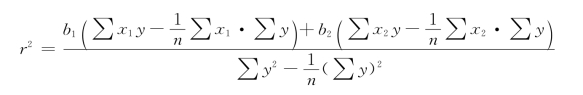
根据表7-8资料计算得

判定系数r2为0.947-5,表明某地区玻璃销售量的变动中有94.75%是由汽车产量和建筑生产值的变动引起的,只有5.25%是由于其他干扰因素引起的。
2.估计标准误差
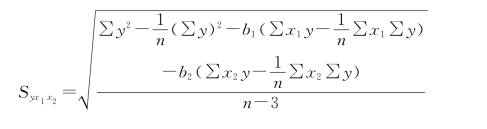

免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







