（一）简单直线回归分析的特点

1.在两个变量之间进行回归分析时，必须根据研究目的，具体确定哪个是自变量，哪个是因变量。

2.在两个现象互为根据的情况下，可以有两个回归方程——y倚x回归方程和x倚y回归方程。

3.回归方程的主要作用在于给出自变量的数值来估计因变量的可能值。一个回归方程只能作一种推算，推算的结果表明变量之间的具体的变动关系。

（二）简单直线回归方程的确定

1.基本方法。简单直线回归方程对于一元一次回归方程，其基本形式是

y倚x回归方程：yc=a+bx

x倚y回归方程：xc=c+dy

a和c是两条直线的截距，b和d是两条直线的回归系数。a，b，c，d都是待定参数。估计这些参数可有不同的方法，统计中使用最多的是最小平方法，用这个方法求出的回归线是原资料的最合适线。就y倚x回归线来讲

这里讨论的最小平方法与本书第四章“动态数列”中长期趋势测定的最小平方法是同一方法。实际上，长期趋势测定也是回归法的一种，那是把时间作为自变量、动态指标作为因变量计算的。因此，那里讲的有关公式，这里都适用，只要把时间变量的符号t改为自变量x或自变量y即可。两个标准方程式写成

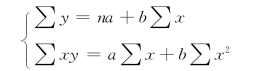
从以上联立方程中解出a和b

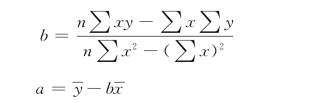
我们可以利用这两个公式算出a和b，从而得出y倚x回归方程yc=a+bx。与此对应的x倚y回归方程的两个参数的公式是：

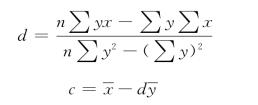
得出的回归方程是x=c+dy。

如果已用积差法计算了相关系数，有相应的资料，也可以用如下的方法求解

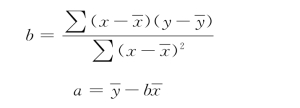
2.简单直线回归方程的计算

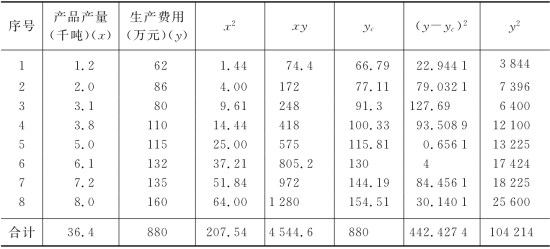
我们仍用表7-2的资料计算出如下数据

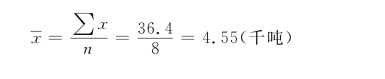
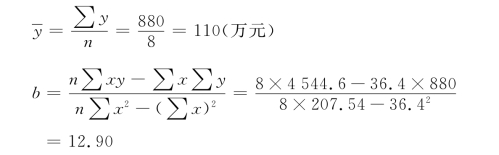
表7-7　简单直线回归方程计算表

把b和a值代入回归方程yc=a+bx

则yc=51.31+12.90x

（三）判定系数r2

用最小平方法求得的回归直线yc=a+bx确定了x与y的具体变动关系。但是，实际值是不是紧密分布在其两侧？其紧密程度如何？这关系到回归模型的应用价值。因此，对回归值的拟合优度必须加以测定。判定系数r2便是测定回归直线拟合优度的一个重要指标。

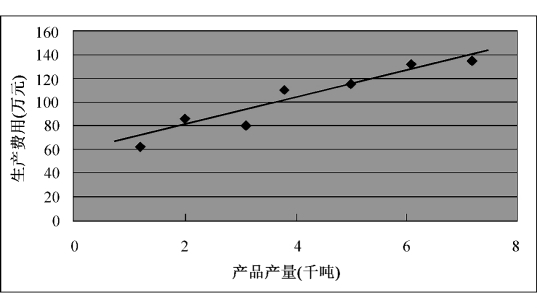
图7-4　8个企业产量和生产费用的直线回归方程图

线性回归方程拟合优度的好坏实质上就是回归方程误差大小的问题。总体来看，即指所有因变量的实际值y与平均值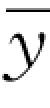的偏差。为了说明，我们来看线性回归方程误差的分解图（见图7-5）。

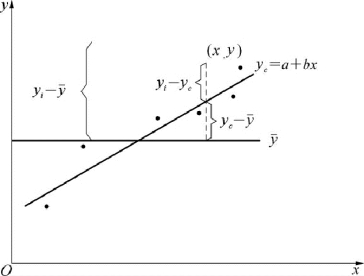
图7-5

判定系数r2的计算，在实际工作中，采用以下简捷公式：

在简单直线回归模型中，判定系数即为单相关系数的平方。(www.daowen.com)

根据表7-7资料，得：

（四）估计标准误差

直线回归是在直线相关条件下，反映变量之间一般数量关系的平均线。根据直线回归方程，知道了自变量的数值，就可以推算出因变量的数值。但是，推算出来的因变量的数值并不是精确的数值，它是一个估计值，和实际值之间有差异。如表7-7所示，产品产量3.1千吨，生产费用的实际值80万元，预测值为91.3万元，两者相差11.3万元，即（y-yc）=-11.3万元。我们不仅用回归方程推算已有实际值的估计值，还要推算未知的值。这样就有了推算的数值与实际值相差多大的问题。如果差距小，说明推算结果准确性高；反之，则低。为了度量y实际值和估计值离差的一般水平，可以计算估计标准误差。

估计标准误差就是用来说明回归方程推算结果的准确程度的统计分析指标，或者说是反映回归直线代表性大小的统计分析指标。

估计标准误差有两种计算方法。

1.根据因变量实际值和估计值的离差计算

计算公式如下

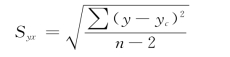
公式中的Syx代表估计标准误差。估计标准误差和有两条回归直线一样，也可以计算两个，另一个估计标准误差可以用Sxy表示。

式中，y——因变量数列的实际值；

yc——是根据回归方程推算出来的估计值。

所以y-yc是因变量实际值和估计值的估计误差，如果将估计误差总和相加，结果是∑（y-yc）=0。

式中，n——因变量的项数。

由于在∑（y-yc）2=∑（y-a-bx）2公式中，其中参数a和b是由实际资料计算的，从而丧失了两个自由度。

从计算公式可以看出，计算的结果实际上也是个平均误差。但不是简单平均的，而是经过乘方、平均、再开方的过程，这和标准差的计算过程一样。它的作用是说明估计的准确程度，所以叫作估计标准误差，也可叫作估计标准差或回归标准差。根据表7-6的资料可得

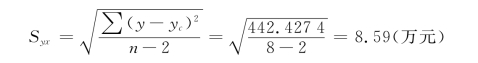
计算结果显示，估计标准误差为8.59万元。这个数值越大，就表明估计值的代表性越小，也就是相关点的离散程度越大；这个数值越小，则说明估计值的代表性越大，也就是相关点的离散程度越小。如果Syx=0，就是y和yc没有差异，从相关图上看，则表明所有的相关点全在yc这条直线上，说明估计值完全准确。

2.根据a、b两个参数值计算估计标准误差

上述计算估计标准误差方法是用平均误差来表现的，但是计算比较麻烦，须计算出所有的估计值。如果已知直线回归方程的参数值，有一个比较简便的计算方法。计算公式如下

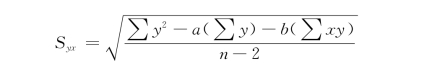
根据表7-5资料，得

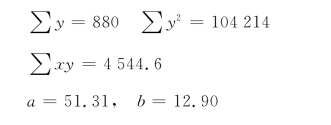
代入公式

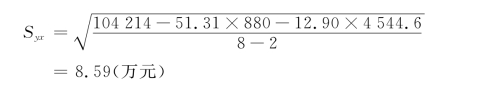
（五）线性回归方程的显著性检验

我们利用随机观测到的几对有关x与y的样本数据，采用最小平方法得到的回归系数b是否符合回归方程的基本假设，需要进行检验。回归系数b与0是否有显著差异，表明总体回归系数β是否为0。若β=0，总体回归线就是一条水平线，x与y之间无线性关系，违背了一元线性回归方程的基本假设；若β≠0，即x与y之间存在着线性关系，符合假设条件，所建立的一元线性回归方程可以认为符合变量间的变化规律。对回归系数b的检验就是要验证变量x与y之间是否真正存在线性关系，一般采用t检验，其步骤如下：

（1）假设观测的样本是从一个没有线性关系的总体中选出的，即：

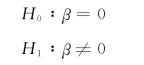
（2）计算回归系数b的检验统计量t值：

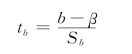
式中，Sb是回归系数b的标准差，计算公式为：

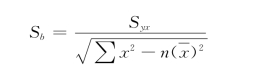
式中，Syx是估计标准误差。

（3）根据给定的显著水平α和自由度（n-2），查t分布表中相应的临界值tα／2。

（4）做出判断：将计算的统计量与临界值tα／2对比，若|tb|＞tα／2，则拒绝H0，表明变量间线性相关关系在统计上是显著的；若|tb|≤tα／2，则接受H0，说明变量间线性相关关系在统计上并不显著。

根据表7-7资料我们得：

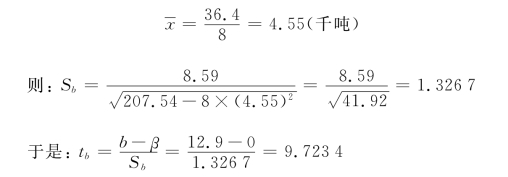
若取α=0.05，n-2=8-2=6，查t分布表（见第六章附表3）得

|tb|＞tα／2=2.447，表明回归系数b=0的可能性小于0.05，即5%，因而拒绝H0，得出β≠0的结论。说明回归系数是显著的，在相关系数检验的基础上进一步证明了产品产量和生产费用之间存在线性关系，产量是影响生产费用的显著因素。