在对两个变量x与y进行线性相关分析时，当某些现象间并无相关关系时，通过样本数据计算，有时也能得到一个比较大的r值，这时就会产生虚假的相关系数。为什么会出现这种情况呢？在实际的分析研究中，往往是利用一个区段或时段的样本数据，根据其对应值计算r值，因而带有一定的随机性，并受抽样误差的影响，而且样本容量越小，随机性越大，其可信程度就越差。相关关系能否真实地表现变量总体的相关关系受到随机因量和样本容量大小的影响。在作出结论之前，有必要检验样本的r值是否可能来自一个不存在线性相关的总体（即ρ=0，ρ为总体的相关系数），即r的显著性检验。

通过r值在统计上是否显著，可以说明它能否作为两个变量间存在线性关系的依据：若r在统计上是显著的，就证明两个变量间存在线性关系；反之，则说明两个变量之间不存在线性关系。

对于线性相关，为了评价相关系数的显著性，在小样本（n＜30）情况下，通常采用t分布来检验r的显著性。其方法和步骤如下：

第一步：提出假设。假设样本是从一个不相关的总体中抽出的，设

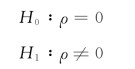
第二步：给定显著性水平α，并依据自由度（n-2），查找t分布表中相应的临界值tα／2（n-2）。

第三步：计算检验的统计量：

第四步：做出判断。将计算的统计量t与临界值tα／2（n-2）对比，若|t|＞tα／2（n-2），则拒绝原假设H0，表明总体的变量间线性相关关系在统计上是显著的；若|t|＜tα／2（n-2），授受原假设H0，表明变量间线性相关关系在统计上并不显著。

例如，一名心理学家获得了10名工人的智商值和劳动生产率的数据，其结果列为表7-6，试计算智商值与劳动生产率之间的相关系数r，并对r进行显著性检验（α取0.05）。(www.daowen.com)

表7-6　相关系数计算表

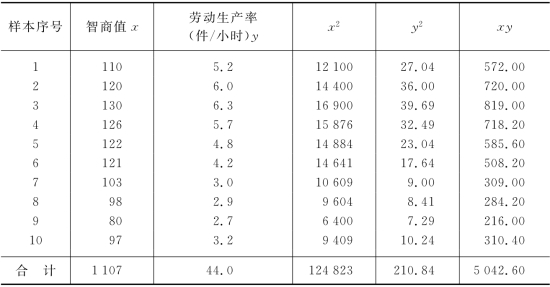
根据表7-6资料，计算相关系数：

r=0.867为高度相关。检验智商和劳动生产率之间的相关系数是否显著。

提出假设：

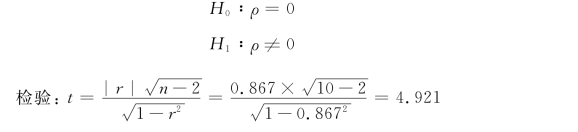
若取α=0.05，自由度n-2=8，查t分布表（见第六章附表3），则tα／2=2.306。

由于t=4.921＞tα／2（n-2）=2.306，所以拒绝原假设H0，即样本相关系数r是显著的，说明智商值与劳动生产率之间确实存在线性关系。