（一）相关分析主要内容

相关分析是用以分析社会经济现象间的依存关系，其目的就是从现象的复杂关系中消除非本质的偶然影响，从而找出现象间相互依存的形式和密切程度以及依存关系变动的规律性。这在实际工作中运用得非常广泛。相关分析的主要内容如下：

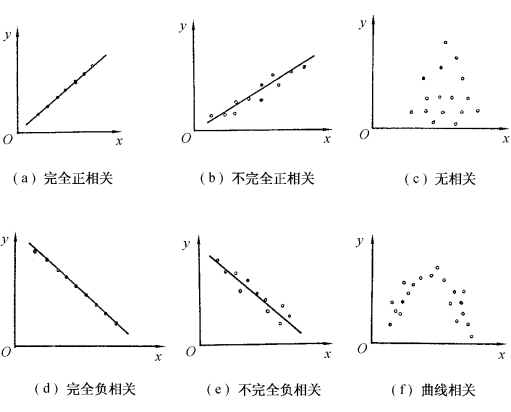
图7-1　相关关系类型

1.确定现象之间有无关系，以及相关关系的表现形式

这是相关分析的出发点。有相互依存关系才能用相关方法进行分析，没有关系而当作有关系会使认识发生错误。关系表现为什么样的形式就需要使用什么样的方法分析，把曲线相关当作直线相关来进行分析，也会使认识发生偏差。

2.确定相关关系的密切程度

相关分析的目的之一，就是从不严格的关系中判断其关系的密切程度。判断的主要方法，就是把自变量和因变量的数据资料编制成散布图或相关表，帮助我们作一般分析，判断相关的密切程度，进而计算出相关系数。

（二）回归分析主要内容

回归这个统计术语，最早采用者是英国遗传学者高尔登，他把这种统计分析方法应用于研究生物学的遗传问题，指出生物后代有回复或回归到其上代原有特性的倾向。高尔登的学生波尔逊继续研究，把回归的概念和数学方法有联系起来，进行回归分析。(www.daowen.com)

回归分析就是通过一定变量或一些变量的变化解释另一变量的变化。其主要内容如下：

1.确定现象之间相关关系的数量模型

确定了现象间确实有相关关系及密切程度，就要选择合适的数学模型，对变量之间的联系给予近似的描述。

如果现象之间的关系表现为直线相关，则采用配合直线的方法；如果现象之间的关系表现为各种曲线，则用配合曲线的方法。可根据自变量选取个数不同，构造一元回归方程和多元回归方程。使用这种方法能使我们找到现象之间相互依存关系的数量上的规律性。这是进行判断、推算、预测的根据。

2.测定变量估计值的可靠程度

配合直线或曲线后，可反映现象间的变化关系，也就是说，自变量变化时，因变量有多大变化。根据这个数量关系，可测定因变量的估计值。把估计值与实际值对比，如果它们的差别小，说明估计得较准确；反之，就不够准确。这种因变量估计值的准确程度，通常用估计标准误差来衡量。

3.预测因变量

对回归方程变量之间的相关性进行显著性检验。通过统计检验后，利用回归模型，根据自变量去估计，预测因变量。

（三）相关分析与回归分析的关系

相关分析是回归分析的基础和前提，回归分析则是相关分析的深入和继续。相关分析需要依靠回归分析来表现变量之间数量关系的具体形式，而回归分析则需安依靠相关分析来表现变量之间数量变化的相关程度。只有当变量之间存在显著相关时，进行回归分析寻求其相关的具体形式才有意义。如果没有对变量之间是否相关及相关方向和程度做出正确判断就进行回归分析，很容易造成“虚假回归”。与此同时，相关分析只研究变量之间相关的方向和程度，不能推断变量之间的相互关系的具体形式，也无法从一个变量的变化来推测另一个变量的变化情况，因此，在具体应用过程中，只有将相关分析和回归分析结合起来，才能达到研究和分析的目的。