（一）总体均值的假设检验

正态总体有两个重要参数：均值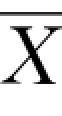和方差σ2。一旦这两个参数确定之后，正态总体就完全确定了。因此，对服从正态分布总体的检验问题，就是检验这两个参数的问题。

1.一个总体均值的假设检验

（1）方差已知时，对总体为正态分布均值的假设检验

当正态总体的方差σ2已知，要检验总体的均值，其原假设为H0∶μ=μ0。而与之相应的替代假设可能有三种，分别是：μ≠μ0、μ＞μ0、μ＜μ0。在检验中替代假设选择哪一种，应根据具体问题而定。

①双侧检验H0∶μ=μ0；H1∶μ≠μ0

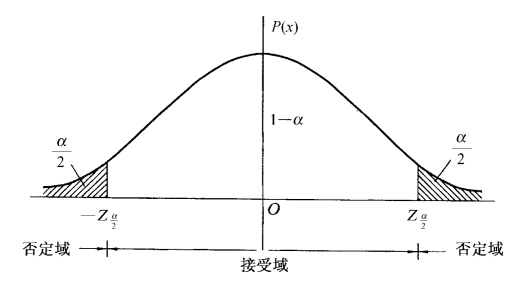
图6-9　双侧检验的否定域和接受域

例如，设我国出口的某品牌水果罐头，标准规格是每罐净重250克。根据以往经验，标准差为3克。现该公司生产一批供出口用罐头，从中抽取100罐检验，其平均重量为251克。按规定显著性水平α=0.05，问该批罐头是否符合出口标准（即净重量为250克）？

在解答这个问题之前，我们首先要了解该问题的经济意义。对于食品罐头而言，规定一个净重是为了保障买卖双方的合理经济利益。如规定净重为250克，当净重远远超过250克时，生产成本增加，卖方吃亏；而净重远远低于250克时，买方如果接收了这批货物就会吃亏。所以需要罐头不过于偏重或偏轻。根据题意拟定原假设为：

其备选假设为：

双侧检验规则为：

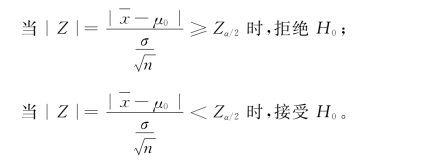
②右侧检验H0∶μ≤μ0；H1∶μ＞μ0

右侧检验适用于原假设H0∶μ≤μ0，而备选假设H1∶μ＞μ0的情况。只要样本平均数显著地超过假设的总体参数，就拒绝原假设H0；而接受备选假设H1。由于拒绝区域在样本平均数分布的右端，所以称之为右侧检验。如用新工艺生产某种产品，产品的使用寿命是否有所提高；当增加了良种比例，某种农作物的平均产量是否有所提高等。这种检验的假设为H0∶μ=μ0；H1∶μ＞μ0。

图6-10　单侧检验的否定域和接受域

例如，某公司生产一种产品，原月产量平均为75台，已知月产量服从正态分布，方差为14。设备更新后，为了考察产量是否提高，抽查了6个月产量，求得平均产量为78，假设方差不变，问在显著性水平α=0.05下，设备更新后的月产量是否有显著提高？

由于总体服从正态分布，且方差已知，可用Z为检验统计量。样本平均值为78，可能是总体平均产量提高了，也可能是从平均产量不超过75的总体中抽出的样本平均数偏高所致，现用假设检验的方法来判断。

如把产量减少作为原假设的话，只要否定原假设，就可说明产量在提高。可用下面假设：

注意：在双侧检验中，原假设只有一个参数值，而单侧检验中的原假设则有大量的参数值。可以证明，如在相等点μ=μ0上否定了H0，则在原假设所含的任何点上也将否定H0。

原假设总体均值不大于75，倘若由样本数据算出的检验统计量Z≥Zα，就可否定原假设H0；否则，就不否定。因此，否定域将位于统计量分布曲线的右尾，在显著性水平α下，尾部的面积为α，临界值为Zα。当α=0.05时，对应的临界值为Z0.05=1.645，统计量的值为

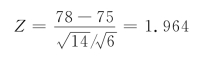
因为Z＞1.645（见本章附表），故否定原假设H0，这说明设备更新后，月产量有明显提高。右单边拟定假设：

检验规则为：

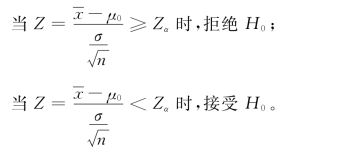
③左侧检验H0∶μ≥μ0；H1∶μ＜μ0

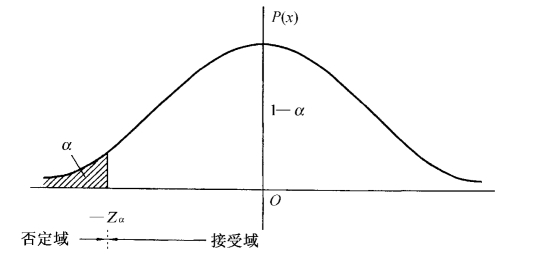
图6-11　单侧检验的否定域和接受域

例如，基于产品转换的时间与成本，某生产主管在说服公司经理采用另一种新生产方法时，必须说明新方法能降低成本。目前的生产方法其平均成本为500元，标准差为20元，新方法试行了一段时间，发现25个产品的平均成本为480元，且方差不变。假定产品的成本服从正态分布，试以α=0.05的显著性水平决定该公司是否转换新的生产方法。

为了决定新方法是否确能降低成本，我们考虑下面的统计假设：

由于总体服从方差已知的正态分布，所以在原假设下，用检验统计量

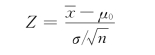
它服从标准正态分布。

当α=0.05时，对应的临界值为-Z0.05=-1.645（见本章附表），统计量值为

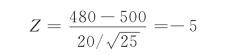
因为Z=-5＜-1.645，故拒绝原假设H0，即说明新方法确能降低生产成本，公司经理应采用新方法。左单边拟定假设：

检验规则：

当总体为非正态分布，且样本为大样本，即样本容量为n＞30时，根据中心极限定理，我们也能用Z近似地作为检验统计量。

（2）方差未知时，对总体为正态分布均值的假设检验

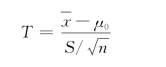
这个统计量服从自由度为n-1的t分布。

利用服从t分布的统计量去检验总体均值的方法称为t检验法。其具体做法是：根据题意提出假设；构造检验统计量T并根据样本信息计算其具体值；对于给定的显著水平α，由t分布表查得临界值；将所计算的T值与临界值比较，做出检验结论。

给定显著性水平α，对于三种不同备选假设其拒绝区域分别是：

①若H1∶μ≠μ0，查t分布表可得临界值tα／2，其拒绝区域为（-∞，-tα／2］和［tα／2，∞）；

②若H1∶μ＞μ0，查t分布表可得临界值tα，其拒绝区域为（tα，∞）；

③若H1∶μ＜μ0，查t分布表可得临界值-tα，其拒绝区域为（-∞，-tα）。

例如，某汽车轮胎公司宣称，该公司一等品轮胎的平均寿命在一定重量和正常行驶条件下大于25-000公里。对一个由15个轮胎组成的随机样本进行试验，得到的平均值和标准差分别为27-000公里和5-000公里。假定轮胎寿命近似服从正态分布，试问是否可以相信产品同公司所说的标准相符？（α=0.05）

要对汽车轮胎公司所说的标准取得强有力的支持，必须把不符合标准作为原假设，而把符合标准作备选假设。于是建立假设

由于总体近似服从正态分布，总体方差未知，所以其观测值为

查t分布表得，t0.05（14）=1.76（见本章附表3）。由于T＜t0.05（14），所以只能接受H0，也即没有充分的理由相信汽车轮胎公司所说的标准与实际相符。

T检验适用于小样本（n＜30）情况下总体方差未知时对正态总体均值的假设检验。随着样本容量n的增大，t分布趋近于标准正态分布。所以大样本（n＞30）情况下，总体方差未知时对正态总体均值μ的假设检验通常近似采用Z检验。(www.daowen.com)

2.两个总体均值之差的假设检验

从两个相互独立的被研究总体中，各随机抽取一个样本。如果这两个样本平均数之间存在差异，是否能说明它们的总体平均数之间也存在着差异？这需要用假设检验的方法进行研究。

对于给定的显著水平α，可查标准正态分布表确定临界值，并给出拒绝域。

对于这个问题，若进行双侧检验，有：

若进行单侧检验，有：

当H0∶μ1≤μ2；H1∶μ1＞μ2时，拒绝域为Z＞Zα

当H0∶μ1≥μ2；H1∶μ1＜μ2时，拒绝域为Z＜-Zα

如果两个样本容量均超过30，可采用Z检验统计量。其计算公式为：

我们假设：

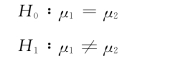
根据已知条件，计算检验统计量

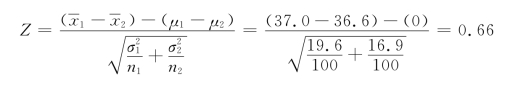
查正态分布分位数表，临界值Zα／2=±1.96

因为-1.96＜Z=0.66＜1.96，落入接受域，所以接受原假设，即有理由认为A、B两企业生产的圆钢平均抗拉强度不存在显著差异。

（二）总体成数的假设检验

1.一个总体成数的假设检验

对总体成数的假设检验实际上是对两点分布总体均值的检验，所以必须在大样本条件下进行检验，其检验步骤与Z检验法相同，只是统计量不相同。

当我们要检验总体的成数是否等于某一常数时，其假设为

（1）H0∶P=P0，H1∶P≠P0；

（2）H0∶P≤P0，H1∶P＞P0；

（3）H0∶P≥P0，H1∶P＜P0。

若H1∶P≠P0，当|Z|≥Zα／2，拒绝原假设，否则接受原假设；

若H1∶P＞P0，当Z≥Zα，拒绝原假设，否则接受原假设；

若H1∶P＜P0，当Z≥-Zα，接受原假设，否则拒绝原假设。

例如，据最近一次人口普查资料获悉，某地区人口中，具有大学文化程度的人口占1.2%。现从该地区人口中随机抽取5-000人的样本，其中具有大学文化程度的为80人。试问在显著性水平0.05下，目前调查结果的比例与普查时的比例是否有显著不同？

该问题是现在大学生比例数与普查的1.2%相比是否有显著不同。假如有显著不同，低于或高于这个数值都是有可能的。因此这属于总体成数的双侧检验。

假设　H0∶P=1.2%

H1∶P≠1.2%

给定的显著水平α=0.05。由于是双侧检验，查正态分布分位数表得临界值Zα／2=1.96，检验统计量的样本观测值为：

由于Z＞Z0.025=1.96，所以拒绝H0，这表明目前该地区人口中，大学文化程度的人数所占比例与普查时有显著差异。

又如，某公司负责人发现开出去的发票有大量笔误，而且断定这些发票中，错误的发票占20%以上。随机抽取400张检查，发现错误的发票有100张，即占25%。这是否可以证明负责人的判断正确？（α=0.05）

按题意建立假设

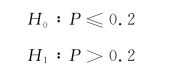
选取检验统计量为

其观测值为

由于α=0.05，查正态分布分位数表得临界值Zα=1.645，因为Z=2.5＞Zα=1.645，故拒绝原假设，即通过检验，以5%的显著性水平，认为这些数据可以证明负责人的判断是正确的。

2.两个总体成数之差的假设检验

①两个总体成数是否相等的假设检验

这个检验等价于检验两个总体成数之差是否为0。这时，可建立假设：

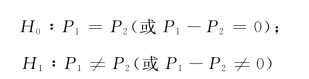
其适当的检验统计量是：

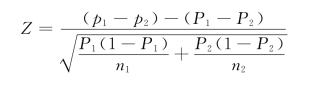
由于真正的总体成数P1和P2并不知道，我们必须对它们做出估计。最适当的估计值通常为样本成数。由于原假设P1-P2=0相当于假设两个总体成数相等，这就有理由将两个样本结果联系起来，得出一个被设定为公共成数的联合估计值：

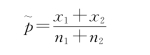
其中，x1和x2分别是两个样本中具有某种特征单位的个数。因此，检验统计量就成为：

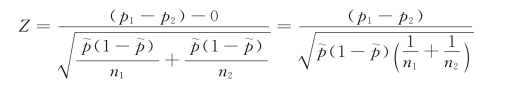
根据经验，一般要求np≥5时，才能用Z统计量。

例如，甲、乙两公司属于同一行业，有人问这两个公司的职工是愿意得到特定增加的福利费？还是愿意得到特定增加的基本工资？在甲公司150名职工的简单随机抽样中，有75人愿意增加基本工资；在乙公司200名职工的随机抽样中，103人愿意增加基本工资。在每个公司，样本容量占全部职工的比率都不超过5%。试在α=0.01的显著水平下，可以判定两个公司中愿意增加基本工资的职工所占比率不同吗？

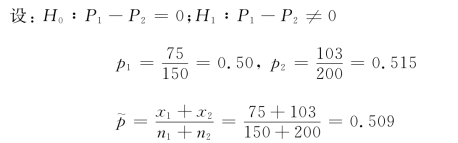
检验统计量的值为：

②两个总体成数之差为某一不为0的常数的假设检验

即：P1-P2=A　（A≠0）

H0∶P1-P2=A；H1∶P1-P2≠A

检验统计量为：

例如，某公司质量检验人员认为该公司A部门的产品一级品率比B部门产品一级品率大5%，现从A部门和B部门分别抽取两个独立随机样本，得到如下数据：nA=150，其中一级品数为113；nB=160，其中一级品数为104。根据这些数据检验质量研究人员的观点（设α=0.05）。

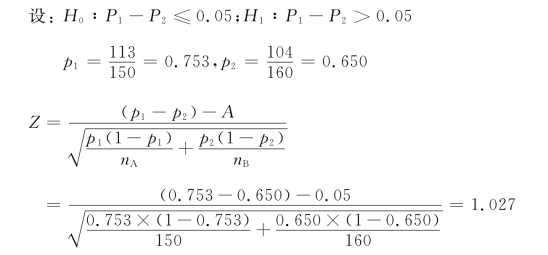
这是右侧检验。α=0.05，Zα=Z0.05=1.645，由于Z＜Zα，即1.027＜1.645，所以不能否定原假设H0，即我们不能说该公司质量检验人员的观点是真实的。