（一）假设检验的一般步骤如下：

第一步：建立统计假设。根据研究问题的需要提出原假设H0和备选假设H1。

在假设检验中，称所要检验的假设H0为原假设（Null　hypothesis），称H1为备选假设（Alternative　hypothesis），若原假设被拒绝，备选假设就被接受。拒绝原假设的区域称为拒绝域（Rejection　region），拒绝域之外的区域即为接受域（Acception　region）。原假设的提出一般有三种方式，以总体均值的检验为例：

（1）H0∶μ=μ0，H1∶μ≠μ0

（2）H0∶μ≤μ0，H1∶μ＞μ0

（3）H0∶μ≥μ0，H1∶μ＜μ0

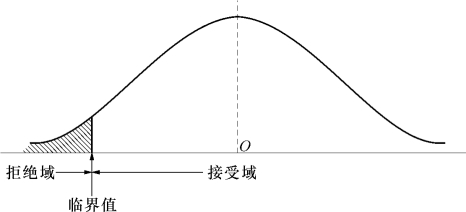
具体采用哪种方式需根据具体情况而定。若采用第一种方式，则拒绝域在分布曲线的两侧，称为双侧或双边检验，如图6-6所示；若采用后两种方式，则拒绝域位于分布曲线的右侧或左侧，称为单侧或单边检验，如图6-7和图6-8所示。

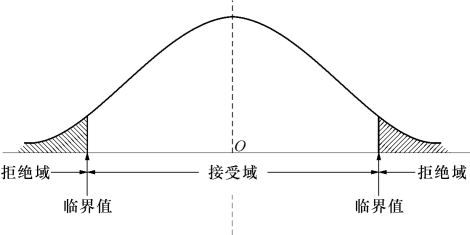
图6-6　H0∶μ=μ0

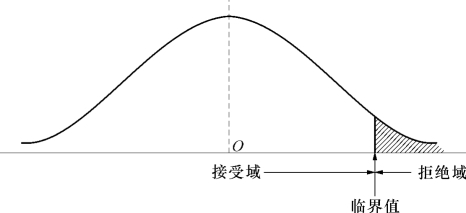
图6-7　H0∶μ≤μ0

(www.daowen.com)

图6-8　H0∶μ≥μ0

第二步：确定假设检验的样本统计量及其分布。假设检验与参数估计一样，需要通过样本统计量进行推断，用于假设检验的统计量称为检验统计量。原假设和备选假设确定之后，要构造一个统计量来决定是否拒绝原假设、接受备选假设。在具体问题中，选择的统计量需要考虑总体方差已知或未知，样本属于大样本还是小样本，等等。

第三步：规定显著性水平α值。检验样本统计量确定后，就要利用该统计量的分布以及根据实际问题所确定的显著性水平，来进一步确定检验统计量拒绝原假设的取值范围。由于假设检验是根据样本信息对总体情况进行判断，因此，存在误判的可能。若原假设正确却被当成错误而被拒绝，统计上把犯这种错误的概率α称为假设检验中的显著性水平（Significant　Level）。α的取值人为确定，通常取α=0.05或α=0.01等。

第四步：确定临界值。按照规定的显著性水平和样本统计量的分布性质，确定接受域和拒绝域的临界值（Critical　Value）。

第五步：计算检验统计量的值。根据样本数据计算出检验统计量的值。

第六步：做出统计决策。将检验统计量的值与临界值进行比较，做出拒绝或接受原假设的决策。

在给定的显著性水平α下，检验统计量的可能取值范围被分成两部分：拒绝原假设的区域与不能拒绝原假设的区域。所谓拒绝区域，就是在原假设成立的前提下，其发生概率不超过显著性水平α的区域，如果检验统计量的取值落在这一区域，表明发生了小概率事件（假设检验中的“小概率原理”认为：小概率事件在一次试验中几乎不可能发生），即原假设成立的概率很小，所以应当拒绝原假设，接受备选假设。所谓不能拒绝区域，就是在原假设成立的前提下，其发生的概率在1-α的区域。如果检验统计量的取值落入该区域，表明在原假设成立的前提下，其发生的概率尚不够小，即认为没有充分证据证明备选假设结论为真，所以还不能拒绝原假设。

（二）假设检验的特点

1.反证法思想

假设检验反证法思想就是，先假定“H0为真”，如果检验中出现不合理现象，则表明“H0为真”的假设是错误的，应该拒绝H0。如果检验中未出现不合理现象，则认为“H0为真”的假设是正确的，应该接受H0。

2.小概率原理

大数法则告诉我们，就大量观察而言，事件发生仍是具有规律性的。这种规律性的数量表示被称作概率。在大量观察中频频出现的事件具有较大概率，出现次数较少的事件，具有较小的概率。根据概率大小，人们对它的态度和处理方式是很不一样的。在日常生活中，人们习惯于把概率很小的事件，当作在一次观察中是不可能出现的事件。如飞机失事、火车出轨等都是小概率事件，但人们不会因为有过这类事故就不乘飞机或火车。因为这些事故发生的概率很小，大家都认为它不可能发生。假设检验中所依据的小概率原理，只是把小概率的标准，定得更为具体和数量化而已。通常做法是根据实际问题的要求规定一个显著性水平α（0＜α＜1），当一个事件的概率不大于α时，即认为它是小概率事件。α通常可取0.1，0.05，0.025，0.01，…