（一）机械抽样的概念和作用

机械抽样又称等距抽样或系统抽样，它是对研究的总体按一定的顺序排列、每隔一定的间隔抽取一个单位、并把这些抽取的单位组成样本进行观察的一种抽样方法。

设总体有N个单位，现须抽取一个容量为n的样本，其抽选方法是先将N个总体单位按一定顺序进行排列，令k=N／n，k称为抽样间隔或抽样距离，这实际上把总体单位分成n段，每段中有k个单位，然后在1-k中随机地抽取一个随机数，设为i，则第n个单位为抽中单位以后每隔k个单位为一抽中单位，即第i+k，i+2k，…，i+（n-1）k，直到抽满n个单位为止，如图6-4所示。

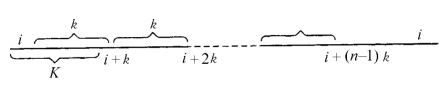
图6-4　机械抽样示意图

机械抽样作用：

1.简便易行。就简单随机抽样来说，在抽样之前须对每个单位加以编号，然后才能利用随机数码表等方法抽选样本，当总体单位很多时，编号与抽选也都比较麻烦。就等距抽样而言，只要确定了抽样的间隔和起点，整个样本的所有单位也随之自然确定。它可以利用现成的各种排列，如某市的工业企业可以按照有关系统和部门的习惯顺序排列，抽样时就可以直接利用这些顺序进行等距抽样。这种抽样方法也便于推广，为不熟悉抽样调查的人员所掌握，也适合某些基层现场的抽样调查。例如，在森林调查中，常常很难在林地中划分抽样单位，然后随机抽选，而机械抽样就比较方便。

2.机械抽样的误差大小与总体单位的顺序有关。因此，当对总体的结构有一定了解时，可用已有的信息对总体进行排列后采用机械抽样，就能提高抽样效率。在一般情况下，等距抽样使本单位在总体中散布比较均匀，其抽样平均误差要小于简单随机抽样。因此，这是大规模抽样调查中一种比较常用的抽样方法。

（二）机械抽样按排队所依据的标志不同，分为无关标志排队法和有关标志排队法

1.按无关标志排队是指排队的标志与调查的内容无关。例如，调查职工生活水平时，职工按姓氏笔画排队；对产品进行质量检查，按产品入库顺序排队等都是按无关标志排队。

2.按有关标志排队是指排队的标志与调查的内容有关。例如，对耕地的农产量进行调查，把地块按往年平均亩产的高低进行排队；对职工家庭生活水平进行调查，把职工按工资水平的高低进行排队等都是按有关标志排队。

（三）机械抽样按样本单位抽选的方法不同，分为随机起点等距抽样、半距起点等距抽样和对称等距抽样

1.随机起点等距抽样。当抽取间隔k确定以后，在第一组随机抽选一个样本单位，设该样本单位的顺序号为a，则第二个样本单位的顺序号为k+a，第三个样本单位的顺序号为2k+a，其余类推，第n个样本单位的顺序号为（n-1）k+a。

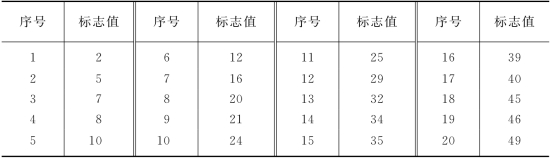
当总体按无关标志排队时，随机起点等距抽样是可以应用的。当总体按有关标志排队时，随机起点等距抽样会产生系统性误差。举例说明，设总体有20个单位，按标志值高低排队编号见表6-9所示。

表6-9　总体单位数按标志值大小排队表

无论按有关标志排队还是按无关标志排队，都可以采用这种方法，这种方法的优点是简单易懂、易于实践。当总体按有关标志排队时，采用这种方法能保证样本有充分的代表性，长期以来在大规模社会经济调查中被广泛运用，实际检验其效果也是令人满意的。

但半距起点等距抽样也存在一定的局限性。首先，随机性不明显，当总体排队确定，样本容量确定，则样本单位也随之确定了。其次，只能抽取一个样本，不能进行样本轮换，抽样的利用率太低。

3.对称等距抽样。要求在第一组随机抽取第一个样本单位，假设该单位的顺序号为a，在第二组与第一个样本单位对称的位置抽取第二个样本单位，它的顺序号为2k-a。在第三组与第二组样本单位对称的位置抽取第三个样本单位，它的顺序号为2k+a。以后抽出的样本单位序号依次为（4k-a）、（4k+a）、（6k-a）、（6k+a）、……

对称等距抽样保留了半距起点等距抽样的优点，而又避免了它的局限性，使其优点更加明显。(www.daowen.com)

（四）机械抽样的抽样误差计算公式

无关标志排队法等距抽样近似于简单随机抽样。因此，一般认为可以按简单随机不重复抽样方法计算抽样误差。即

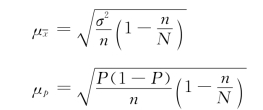
有关标志排队法等距抽样实质上可以看做一种特殊的分类抽样，不同的是分类更细致、组数更多，而在每个组之内则只抽选一个样本单位。因此，一般认为可以用类型抽样不重复抽样的误差公式来计算抽样误差。

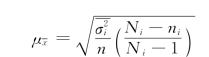
由于在等距抽样时，每个组内只抽取一个单位，因此，ni=1，从而

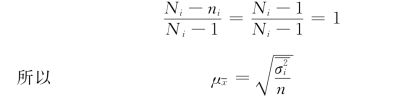
同理，在成数情况下，即用

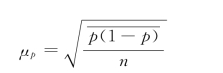
也就是说，等距抽样虽然是不重复的抽样，实质上是使用重复抽样公式。

例如，为了推断15块地甲农作物今年平均亩产，按去年亩产排队，见表6-10所示。

表6-10　某地区甲农作物地块亩产排序表

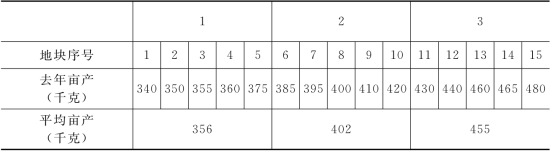
（2）计算各组组内方差

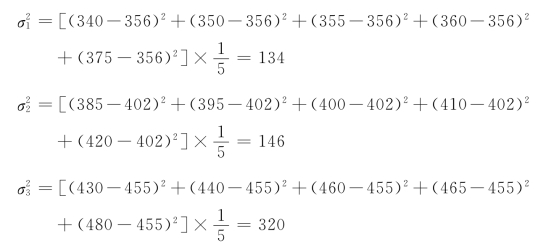
（3）计算平均组内方差

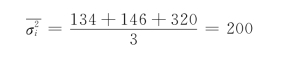
（4）计算抽样平均误差和极限误差

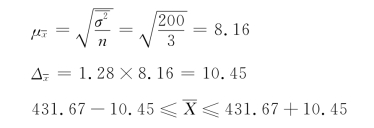
以80%的概率推断平均亩产为421.22～442.12千克之间。