（一）点估计

点估计也叫定值估计（或直接估计），就是把样本平均数或样本成数直接作为总体平均数或总体成数的估计值。

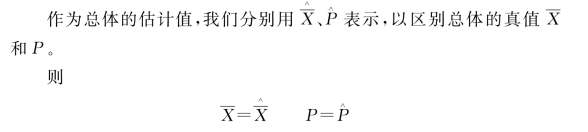
掌握了总体指标的估计值，可以进一步推断总体的总量指标，常用的方法有直接换算法和修正分数法。

1.直接换算法

例如，对某大学在校的6-000名大学生，对其实际月消费支出调查，结果表明，该6-000名大学生的平均消费支出为489元，我们就推断说，该校全体大学生月消费支出为489元。

例如，有一建筑工地，运来一批红砖，抽查400块，发现有4块破损，即样本成数为，则认为所有运来的红砖的破损率也为1%，那么要保证一百万块砖的质量，并考虑砖的破损率，必须运多少砖？则：

1-000　000×1%=10-000，即有1万块破碎，所以要保证工程够用，必须运1-000　000+10-000=1-010　000才能保证工程顺利进行。

直接换算法的优点是简便、易行、原理直观，常为实际工作者所采用。但也有不足之处，即这种估计没有表明抽样估计的误差，更没有指出误差在一定范围内的概率保证程度有多大。要解决这个问题，就必须采用区间估计的方法。

2.修正分数法

修正分数法是指用抽样所得的调查结果同有关资料对比的分数来修正全面统计资料时采用的一种方法。此法要计算：

例如，某市集团公司，2013年年报管理费用为3-218.1万元，现抽查该集团公司14个单位：年报415.03万元，多报0.44万元，少报1.47万元。

（二）区间估计

1.区间估计的意义

在一定概率的保证下，用样本指标去推断总体指标，在考虑抽样误差的前提下，使得总体指标落到某一范围之内，即根据抽样指标定出置信区间和置信度。因这类推断方法有一定理论基础，所以在抽样推断中被广泛应用。

2.抽样极限误差

前面所讨论的抽样平均误差并不是全及指标与抽样指标之间的真实误差，而是这种误差的平均数。由于未知的全及指标是一个确定的量，而抽样指标会随各个可能样本的不同而变动，它是围绕着全及指标上下随机出现的变量。它与全及指标可能产生正离差，也可能产生负离差，这样，抽样指标与全及指标之间就有个误差范围的问题。抽样误差范围就是指变动的抽样指标与确定的全及指标之间离差的可能范围。它是根据概率理论，以一定的可靠程度保证抽样误差不超过某一给定的范围。统计上把这个给定的抽样误差范围叫作抽样极限误差，也称置信区间。

将上面等式经过变换，可以得到下列不等式

(www.daowen.com)

3.可信程度

抽样平均误差μ是表明抽样估计的准确度。抽样误差范围即抽样极限误差Δ是表明抽样估计准确程度的范围。在给定的准确程度范围内的抽样估计，还要研究其估计的可靠程度，即可信程度。

上例说明，抽样误差范围Δ与抽样平均误差μ的关系，即：Δ是用一定倍数的μ表示的抽样指标与全及指标之间的绝对离差。这里的倍数通常用t来表示。t称概率度，它是指以抽样平均误差μ为尺度来衡量的相对误差范围，在数理统计中常称为置信度。用公式表示即

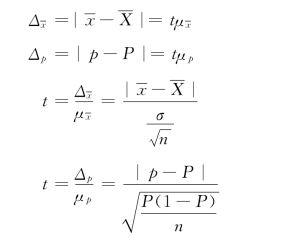
这个公式的意义在于，在一定μ的条件下，当概率度t越大，则抽样误差范围越大，可能样本落在误差范围内的概率越大，从而抽样估计的可信程度也就越高；反之，当t越小，则Δ越小，可能样本落在误差范围内的概率越小，从而抽样估计的可信程度也就越低。

怎样求得样本指标落在一定误差范围内的概率和确定抽样估计的可靠程度呢？数理统计证明，概率度和概率之间保持一定的函数关系，即概率是概率度的函数。用P表示概率以说明抽样估计的可靠程度，其函数关系可表示为

应用正态分布曲线，把概率度t和抽样误差范围Δ联系起来，便可得到抽样推断全及指标在一定范围内的概率保证程度。在统计抽样推断中常用的有（见表6-6所示）：

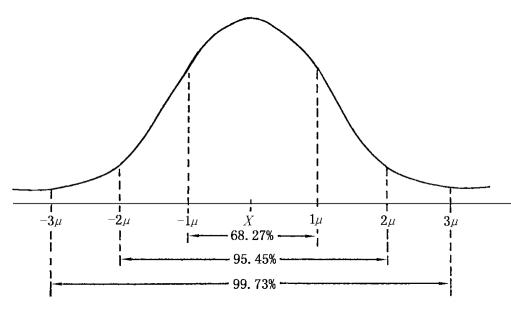
图6-2　正态分布及其曲线下的面积图

表6-6　概率度与概率对照表

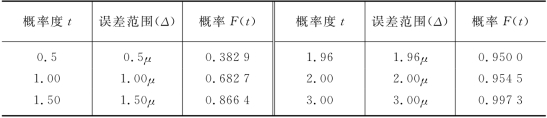
在实际工作中，为计算方便起见，已按不同t值和相应的概率编制专门的正态分布概率表，以供查用。（请见本章后附录）

计算结果表明，有68.27%可靠程度认为该批灯泡的平均使用寿命在1053.21（小时）～1060.79（小时）之间，合格率在89.53%～93.47%之间。

当t=2时，概率保证为95.45%，

计算结果表明，有95.45%可靠程度认为该批灯泡的平均使用寿命在1049.42小时～1064.58小时之间，合格率在87.56%～95.44%之间。

当t=3时，概率保证为99.73%，

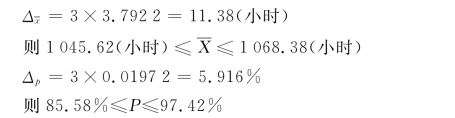
计算结果表明，有99.73%可靠程度认为该批灯泡的平均使用寿命在1045.62小时～1068.38小时之间，合格率在85.58%～97.42%之间。