(一)两因素综合指数的指数体系
1.综合指数体系的一般形式。根据同一个资料计算的数量指标指数和质量指标指数之间存在着一定的联系,形成指数体系,它是综合指数因素分析法的基础。指数体系是:

根据表5-2的资料计算:

分析数字表明:销售额上升17.14%(增加7-200元),是由于销售量上升了14.29%(影响销售额增加6-000元)和销售价格上升2.5%(影响销售额增加1-200元)共同作用的结果。
上面介绍的因素分析法就是一般常用的指数体系分析法,在这种分析中,要从相对数和绝对数两个方面分析两个因素的变化方向(上升或下降)和变动程度(升降多少)构成。
除了上面介绍的这一套常用的指数体系外,还存在着另一套指数体系,其公式为
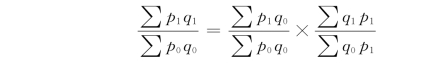
仍用表5-2算例说明:
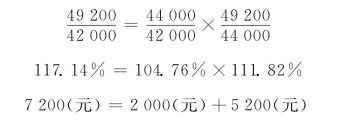
2.平均指标对比指数的指数体系。在平均指标对比指数中,也存在着指数体系,其公式为
可变构成指数=固定构成指数×结构影响指数
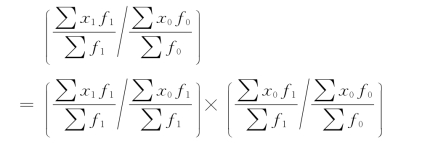
绝对数体系:
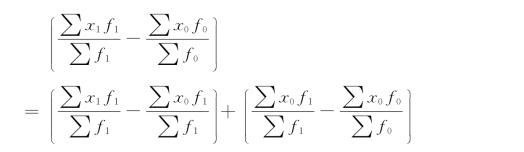
另一套指数体系是:

或
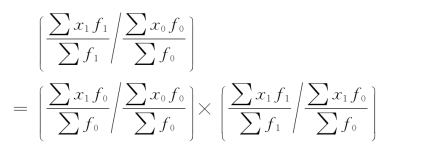

(二)指数体系中的同度量因素的选择和共变影响指数
从上面的分析我们可以看到,在一个指数体系中的数量指标综合指数用基期指标作同度量因素时,质量指标综合指数就要用报告期指标作为同度量因素。反之亦然。因为只有这样,它们之间才能保持数量上的对等关系,因而它们才能配套形成一个指数体系,这是指数因素分析的要求。
因此,从指数体系的观点或因素分析的观点来看,某些指数采用综合指数公式时,仍然可以用报告期指标作同度量因素。不过,由于在指数体系中使用了报告期指标作为同度量因素的指数,就造成了指数体系的内在矛盾,此矛盾表现为相对数指数体系中所反映的因素变动关系与相对应的绝对数体系因素变动关系不一致。这主要是由p和q共变影响造成的,须把它分离出来。
在前面我们已经介绍了共变影响额这个概念,并且进行了计算。现在我们是否可以设想有一个共变影响指数的存在呢?如果有这样的指数,它的表现形式又如何?
我们假定共变影响指数为x,则
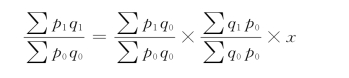
由于
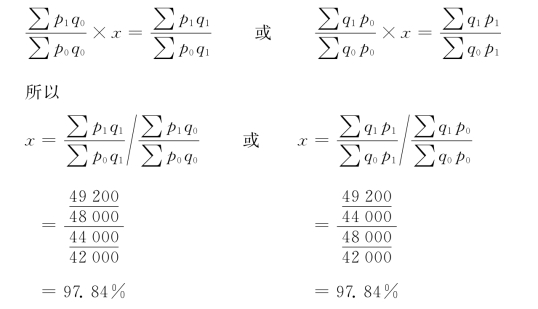
上面两个推算出来的共变影响指数不同,结果相等。
根据表5-2资料计算如下:

用指数体系进行分析
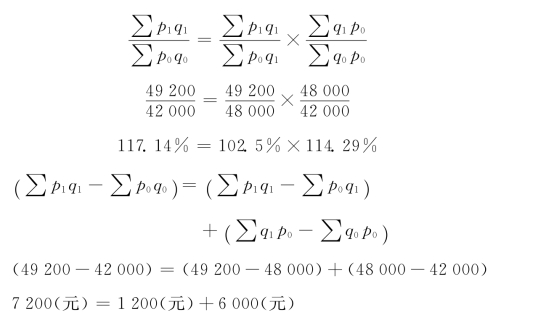
用另一套指数体系进行分析
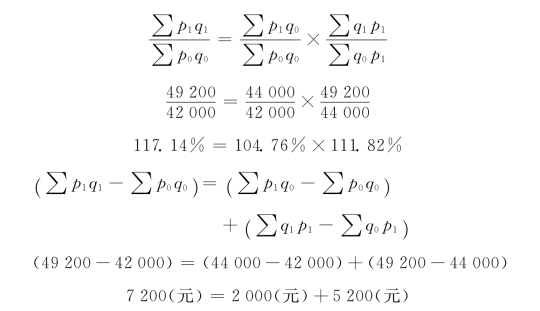 (https://www.daowen.com)
(https://www.daowen.com)
从上面两套指数体系分析来看,无论在相对数的分析上还是绝对数的分析上都不一样。其原因就是因为凡用报告期指标作同度量因素就都包含有“共变影响”在内。
下面我们试用包括有“共变影响指数”在内的指数体系进行计算和分析。
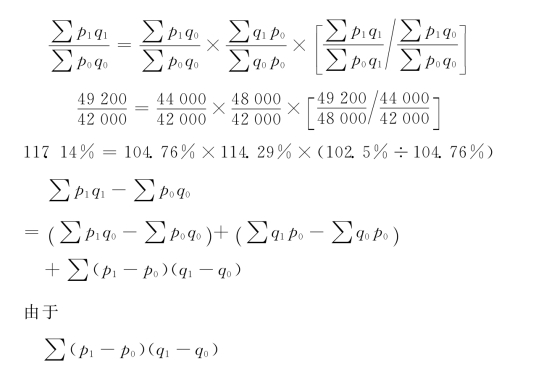
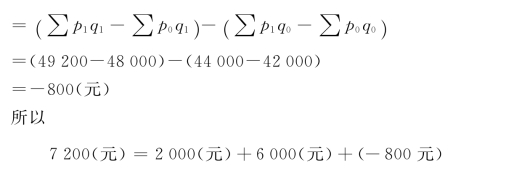
将如上计算用文字说明如下:销售额增长17.14%,是由于物价上涨4.76%,销售量增长了14.29%,销售量和价格同时影响的“共变影响指数”为97.84%,也即由此影响销售额下降2.16%,三者共同作用的结果;销售额增长的绝对额为7-200元,是由于物价上涨使销售额增加2-000元,销售量增加使销售额增加6-000元,由于“共变影响”使销售额减少800元,三者共同作用的结果。
从以上计算可以看出:把综合指数体系分析从两因素增加到三因素,即多一个“共变影响指数”后,初步解决了用报告期指标作同度量因素的综合指数问题。
(三)多因素指数体系
多因素指数体系分析法是在两个因素分析法基础上的深入运用,也就是继续运用数量指标综合指数和质量指标综合指数的编制方法,由表及里对所研究的现象作进一步的深入分析,以测定有关因素在不同时间上的变动程度。在多个因素的指数分析中,采用权数的原则和两因素方法相同,如

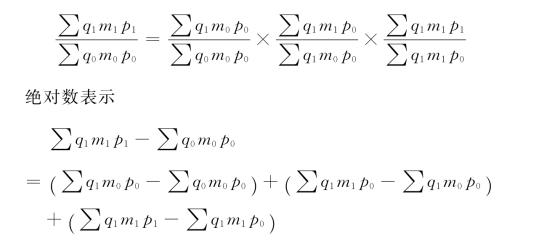
式中,q′——生产消耗量;
q——生产量;
m——单位产品原材料消耗量;
p——单位原材料价格。
例:某企业三种产品的生产量、单位产品原材料消耗量、单位原材料价格及原材料费用总额资料,见表5-9所示。
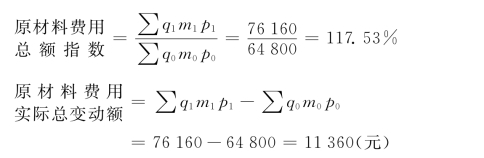
由于报告期较基期原材料费用支出增长了17.53%,使原材料费用多支出11-360元。

表5-9 总量指标变动的多因素分析计算表
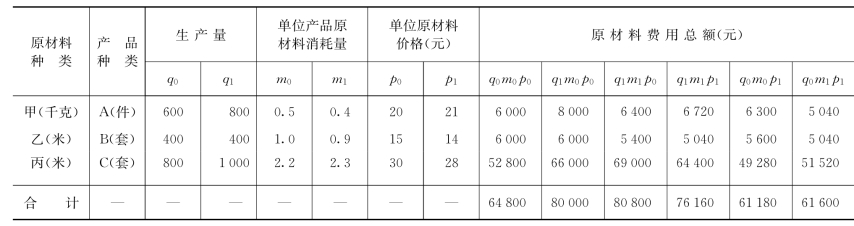
由于产量增长了23.46%,多支出原材料费用15-200元。

由于单位产品原材料消耗量增长了1%,多支出原材料费用800元。

由于原材料单价降低了5.76%,节约原材料费用4-640元。
四个指数之间的关系为
![]()
四个差额之间的关系为
![]()
上述分析表明:“原材料费用总额”报告期比基期多支出11-360元,是由于生产量增加使费用超支15-200元,原材料单耗增加使费用超支800元,原材料单价下降使费用减少4-640元,三者共同作用的结果。
另一套指数体系为
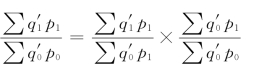
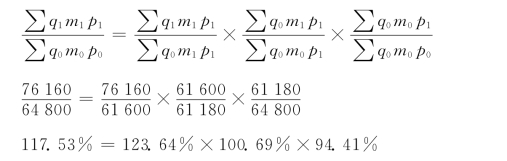
绝对数指数体系
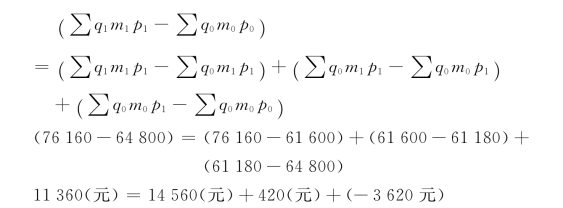
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






