（一）数量指标综合指数公式的建立

数量指标综合指数是说明总体规模变动情况的相对数。例如，商品销售量指数、工业生产指数、农业产品生产量指数、职工人数指数、货物运输量指数等等。

以商品销售量指数为例来说明数量指标综合指数计算公式的形成过程。

如表5-1所示的东方超市三种商品销售量和相应的商品价格资料。

表5-1　东方超市三种商品销售量和商品价格资料

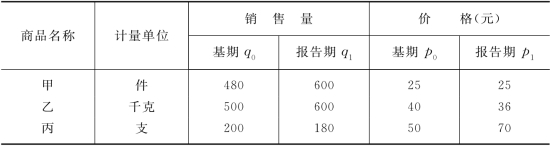
表中，q——物量（生产量、销售量）；

p——商品价格；

下标1——报告期；

下标0——基期。

用k代表个体指数，如果计算三种商品销售量的个体指数，可得

计算结果表明，甲商品的销售量增加了25%，乙商品增加了20%，丙商品减少了10%。

商品销售量指数并非某种具体商品的个体指数，而是反映多种商品销售量的总指数。在编制数量指标综合指数中要注意以下几个问题：

第一，各种商品的度量单位不相同，它们的商品销售量不能直接相加。以基期的商品销售量来讲，甲商品销售480件，乙商品销售500千克，丙商品销售200支。这三种商品的销售量是无法直接相加的。

第二，使用同度量因素，使不能直接相加的指标过渡到能够相加的指标。我们将各个商品销售量乘以商品价格就可以得到商品销售额，即

也即

这里，商品价格叫作同度量因素，它起着媒介作用，将不能相加的商品销售量过渡到能够相加的商品销售额，因而可以形成总销售额∑qp。为了比较，需要分别计算两个时期的总销售额。

第三，为了说明商品销售量的变动，同度量因素必须使用同一时期的，即假定两个时期的商品销售额是按同一个时期的价格计算的。用公式表示就是

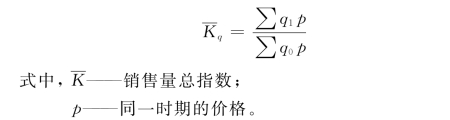
第四，同度量因素（价格）用哪一时期的，是报告期、基期还是用另一种价格？使用不同时期的价格会得到不同的结果，具有不同的经济内容。既然为了突出产量的变动就必须把价格固定下来，也就是分子与分母所乘的价格必须是相同的。那么，究竟用哪种为好呢？对于这个问题统计学术界一向有不同看法和主张，因而就产生了采用不同的同度量因素的各种指数公式。

（二）用基期价格作为同度量因素的综合指数

计算表的形式如表5-2所示。

表5-2　东方超市三种商品销售量综合指数计算表

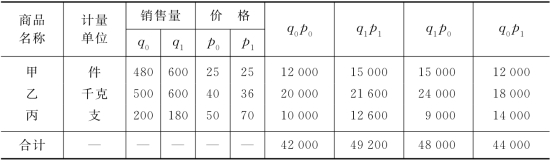
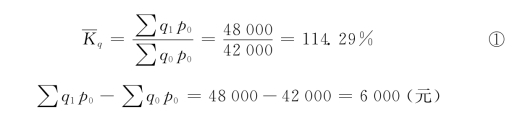
计算结果，商品销售量总指数为114.29%。

商品销售量综合指数的经济内容十分明显，它是两个商品销售额之比，两个商品销售额的数值不同只有一个原因，即各种商品销售量不同。因此，这个公式及其计算结果说明：

1.多种商品销售量综合变动的方向和程度。上例中有三种商品，销售量有增有减，程度不同，总的来讲，商品销售量增长了14.29%。(www.daowen.com)

2.商品销售量变动对商品销售额的影响程度。上例中商品销售量增长了14.29%，也就是说，它的变动使商品销售额增加14.29%。

3.分子和分母相减的差额说明由于商品销售量变动对销售额绝对值的影响。上例中差额为6-000元，即东方超市由于多销售了商品使销售额增加了6-000元。

（三）用报告期价格作为同度量因素的综合指数

如果不用基期价格作为同度量因素，而用报告期价格作为同度量因素，结果就不同，见表5-2所示。

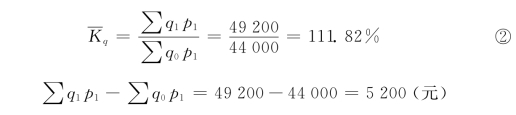
计算结果，无论是对商品销售量的增长程度还是对销售额的影响，都小于用基期价格作为同度量因素的销售量指数。在另外的条件下，也可能产生大于前一个指数的情况。

（四）用不变价格作为同度量因素的综合指数

如用固定价格（不变价格）作为同度量因素，公式为

式中：pn——某一时期的固定价格（不变价格）。

在实际中采用不变价格为同度量因素，即在较长一段时期内，不论计算哪一个时期的数量指标综合指数，都采用某一时期的不变价格作为同度量因素，以消除各时期价格变动影响，保证前后时期之间、地区之间、计划与实际之间指标的可比性。

通过以上三个指数公式的运算产生了这样一个问题，就是同样三种商品，为什么计算出来的商品销售量指数可能各不相同？于是就产生了如何正确选用权数的问题。这个问题比较复杂，现逐一具体分析如下：

先研究下述公式

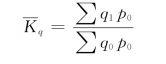
这个公式是早在1864年由德国经济学家埃蒂恩·拉斯贝尔（Etienne　Laspeyres）提出的，故称拉斯贝尔数量指标指数。

这个公式的优点在于用基期的价格p0作权数，也就是假定价格未变动，使产品产量指数在计算过程中不受价格变动的影响，从而可以确切地只反映数量的变化。但这个公式也有缺点，就是容易脱离实际。因为随着生产技术的发展和劳动生产率的提高，新产品不断涌现，老产品常被淘汰或降价，公式中的分子∑q1p0是将报告期商品销售量用基期价格来计算，不但脱离了报告期价格的实际情况，而且有的新产品基期尚未问世，根本就没有基期价格，只能用比价的办法计算，而估算终究是不易准确的，这就影响了指数的准确性。

再研究下述公式

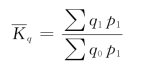
这个公式是1874年德国经济学家哈曼·派许（Herman　Paasche）提出的，故称派许数量指标指数。

这个公式以报告期的价格p1作权数，避免了上述用基期价格作权数而脱离报告期实际的缺点，然而这个公式的主要问题也就产生在采用报告期价格p1作权数的问题上。采用p1作权数，就把价格p0变化到p1这个变动影响带到指数中去了，因而所算得的指数数值就和公式①以p0作权数的指数不相等。因而它不但反映产量的变动，而且通过价格p1对产量的权数作用，还包含了价格变动的影响。将②式加以变换即可看出这个问题。

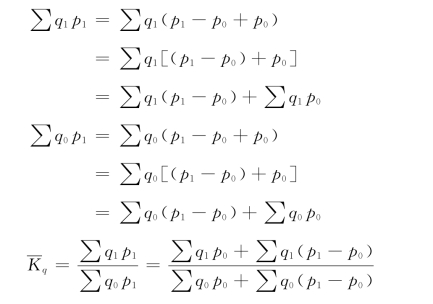
从上面变化了的②式可以大致看出：②式比①式增加了价格变动的因素，即（p1-p0）。这一点从两个指数相应的绝对额间的差量可以明显地看出来。

②式相应的绝对额变动的影响，称为“共变影响额”。

由此可见，②式不仅反映了销售量的变动，它同时还反映了销售量和价格同时变动的影响，也就是包含有价格变动因素在内。

用表5-2的资料计算可得

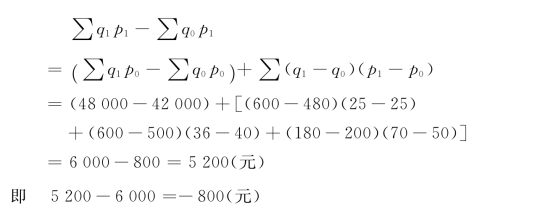
两个公式相应的绝对额之间的差额，正好等于共变影响额。

从指数的定义来看，指数只应该反映销售量的变动，不应该同时又反映价格因素的变动。由此看来，①式比②式好。

上面介绍的销售量指数的计算和分析具有普遍意义，因此，这个问题再推广一步就是在编制综合指数时，数量指标综合指数是用基期质量指标还是用报告期质量指标作同度量因素的问题。结论：在综合指数中，编制数量指标综合指数往往用基期质量指标作同度量因素较好。