应用最小平方法研究现象的发展趋势，就是用一定的数学模型，对原有的动态数列配合一条适当的趋势线来进行修匀。根据最小平方法的原理，这条趋势线必须满足最基本的要求，即原有数列的实际数值与趋势线的估计数值的离差平方之和为最小。用公式表示如下

式中，yc——趋势线的估计数值；

y——原有数列的实际数值。

长期趋势的类型很多，有直线型，也有曲线型，而最小平方法既可用于配合直线，也可用于配合曲线，所以它是分析长期趋势的十分普遍和理想的方法。下面主要介绍根据社会经济现象的基本趋势，如何用最小平方法配合直线方程、抛物线方程及指数曲线方程。

（一）直线方程

如果现象的发展，其逐期增长量大体上相等，则可考虑配合直线趋势。直线方程的一般形式为

式中，a——截距；

b——直线的斜率。

上述直线方程式中，a、b为两个未定参数，根据最小平方法的要求，即∑（y-yc）2→最小值，可用求偏导数的方法，导出以下联立方程组

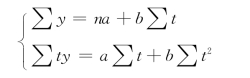
式中，t——动态数列的时间；

y——动态数列中各期水平；

n——动态数列的项数。

为了计算方便，我们可以假设时间t：当时间项数为奇数时，可假设t的中间项为0，这时时间项依次排列为：…，-3，-2，-1，0，1，2，3，…；当时间项数为偶数时，时间项依次排列为：…，-5，-3，-1，1，3，5，…，这时，原点0实际上是在数列正中相邻两个时间的中点。以上两种设t的方法是要使时间项的正负相消，使∑t=0，则上述联立方程组可简化为

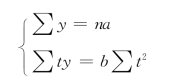
例如，某地区粮食产量资料见表4-18所示。

表4-18　某地区粮食产量　单位：千克

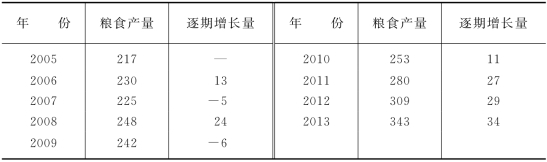
根据表4-18资料初步计算分析，可视为逐期增长量大体相等，所以可配合一个直线趋势方程，现列表说明其计算方法，见表4-19所示。

表4-19　某地区粮食产量直线趋势方程计算表

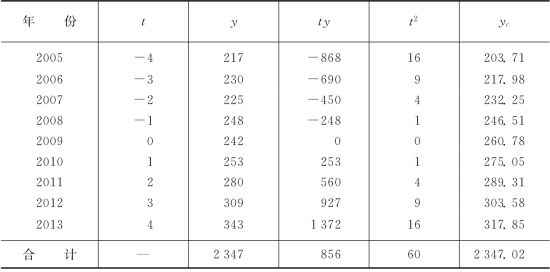
将a、b值代入直线方程式，得

接着把各年t值代入上列方程式，可得各年的趋势值yc，如表4-19最后一栏所示。可见∑yc和∑y的数值非常接近。

如果将趋势直线向外延伸，可预测该地区2016年的粮食产量。也即当t=7时

这个数字可作为经济预测的参考数据。

（二）抛物线方程

如果现象的发展，其逐期增长量的增长量（即各期的二级增长量）大体相同，则可考虑曲线趋势——配合抛物线方程。抛物线的一般方程为

此抛物线方程的二级增长量是相等的，见表4-20所示。

表4-20　抛物线方程计算表

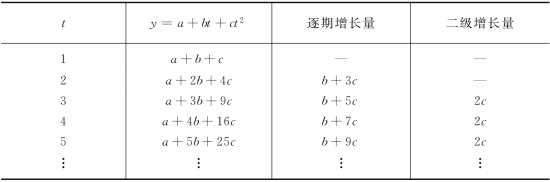
从表4-20看，各期的二级增长量均为2c。

上述抛物线方程式中，有a、b、c三个未定参数，根据最小平方法的要求，同样用求偏导数的方法，导出以下由三个方程组成的联立方程组

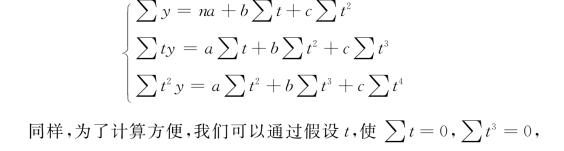
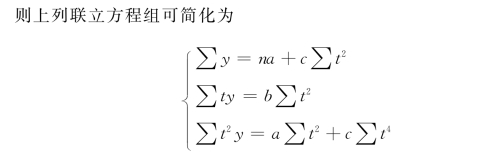
见表4-21所示。

表4-21　某工业产品产量　单位：吨

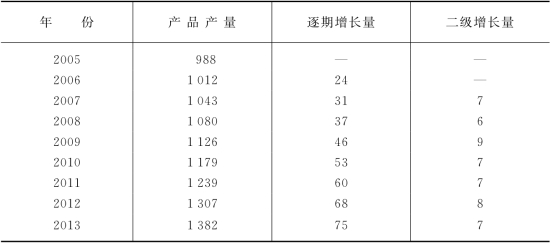
根据表4-21资料初步计算分析，各年二级增长量大体相等，所以该产品产量发展的基本趋势，比较接近于抛物线型，可配合一个抛物线方程。现列表4-22说明其计算过程。

表4-22　某工业产品产量抛物线方程计算表(www.daowen.com)

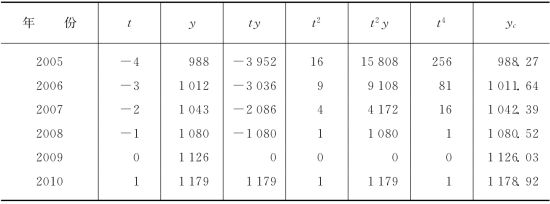
续表

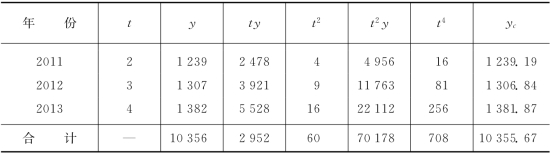
代入上列联立方程组，得

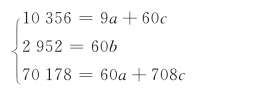
用消元法，解得

将a、b、c值代入抛物线方程，得

如果将这条趋势线向外延伸，可预测该产品2015年产量。也即当t=6时

这个数字可作为经济预测的参考数据。

（三）指数曲线方程

如果现象的发展，其环比发展速度或环比增长速度大体相同，则可考虑曲线趋势——配合指数曲线方程。指数曲线的一般方程为

式中，a——动态数列的基期水平；

b——现象的一般发展速度；

t——动态数列的时间。

a、b均为未定参数。公式表明：t年的变量y等于基期水平乘上一般发展速度的t次方。

进行指数曲线拟合时，一般是将指数方程通过取对数转化成直线方程，然后按直线方程办法确定出参数，再对直线方程求得的结果查反对数表还原。

先对上述方程式两边各取对数，得

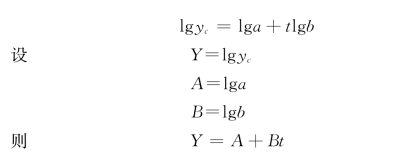
应用最小平方法求得的联立方程组为

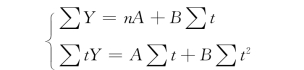
同样设法使∑t=0，则此联立方程组可简化为

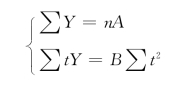
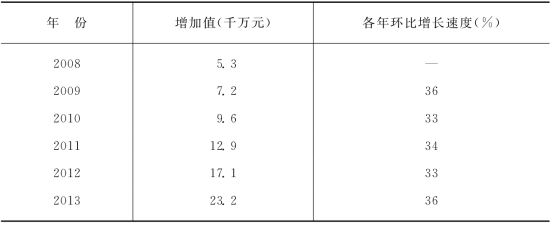
表4-23资料表明各年环比增长速度大体相同，所以该地区工业增加值发展的基本趋势比较接近于指数曲线型，可给本资料配合一个指数曲线方程。

表4-23　某地区工业增加值

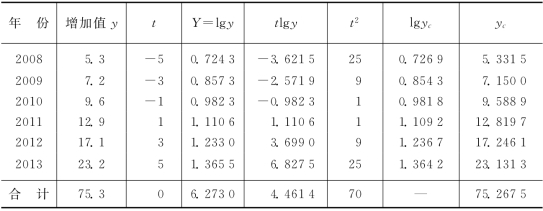
具体计算过程见表4-24。

表4-24　某地区工业增加值指数曲线方程计算表

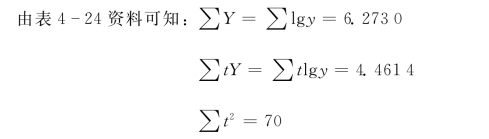
代入上述联立方程组，得

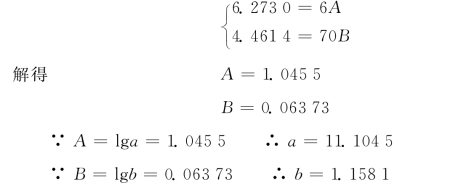
对数趋势直线方程式为：Y=lgyc=lga+tlgb

=1.045-5+0.063-73t

指数曲线方程式为：yc=abt=11.104-5×（1.158-1）t

将代表各年的t值代入上列方程式，就可求得各年的趋势值yc，见表4-24最后一栏所示，由于∑yc数值非常接近于∑y数值，所以此方程拟合较好。

如果将这条趋势线向外延伸，可预测该地区2014年工业增加值。也即当t=7时

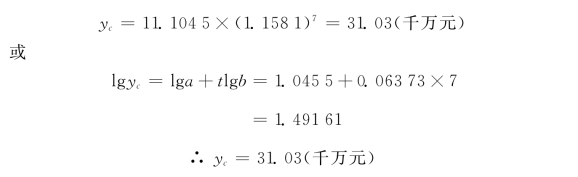
可见，代入对数趋势直线方程预测，计算较为方便。这个数字可作为经济预测的参考数据。

综上所述，我们在分析社会经济现象发展的长期趋势时，应该注意到，不论将哪一种趋势线向外延伸来预测未来可能达到的数值，都具有一定的假定性。因此，要做好经济预测工作，除了用必要的数学方法来建立数学模型外，一定要结合调查研究，具体情况具体分析，才能得出较为准确的结果。