（一）标准差的概念和计算

标准差是测度数据离散程度最重要和最常用的指标。

标准差是各单位标志值与其算术平均数的离差平方的算术平均数的平方根，又称“均方差”。其意义与平均差基本相同，也是根据各个标志值对其算术平均数求其平均离差后再来进行计算的，但由于采用离差平方的方法来消除正负离差，因此在数学处理上比平均差更为合理和优越。通常以σ或S.D.表示标准差，标准差的平方即方差，用σ2表示。标准差的计算公式为

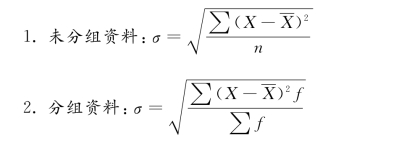
依此公式，计算标准差的一般步骤是：①算出每个变量对平均数的离差；②将每个离差平方；③计算这些平方数值的算术平均数；④把得到的数值开方，即得到σ。

表3-23　某企业工人日产量的标准差计算表

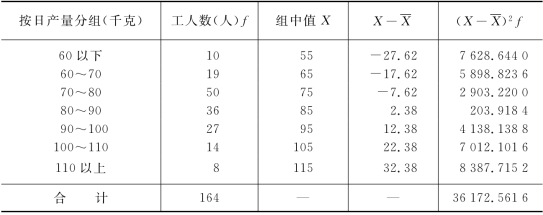
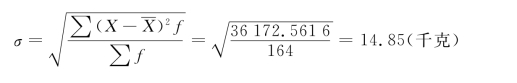
在实际计算中，有时可将上述标准差公式进行变形，这样会更简便些。例如：

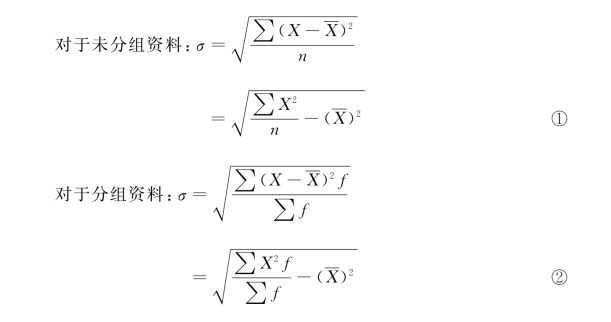
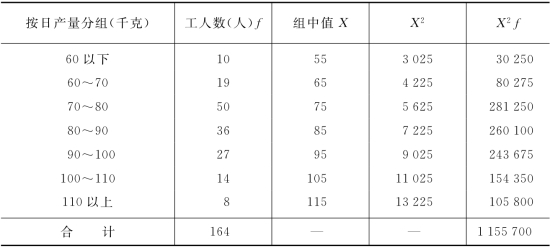
公式①、②是将原来标准差计算中的离差部分简化，可直接根据变量值X、X2进行计算。仍以表3-23资料为例，计算某企业工人日产量的标准差（见表3-24）。

表3-24　某企业工人日产量的标准差计算表

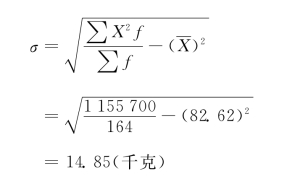
（二）标准差与平均差的数量关系

对同一资料，所求的平均差一般比标准差要小，即：A.D.≤σ。证明如下：(www.daowen.com)

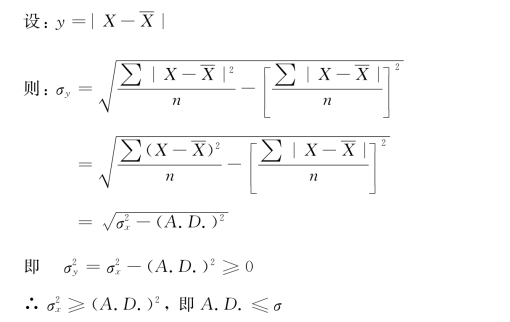
（三）标准差的应用

标准差是统计学中的支柱性概念。在社会经济现象的统计分析中，标准差是反映总体分布离散趋势的重要特征值，在现实生活中具有广泛的应用价值。比如，产品质量检验、教学质量评估等。

1.测定分布偏度

一般情况下，SK＞0为右偏，SK＜0为左偏，SK=0则为对称分布。偏态系数通常取值在-3到+3之间。SK的绝对值大，表明偏度大；反之，则表明偏度小。

2.计算标准分

对于来自不同均值和标准差的总体的个体数据，往往不能直接对比，需要将其转化为同一规格、尺度的数据后再比较。这种转换的方法常常是将数据进行标准化，标准化是通过计算标准分（t）来进行分析的，其计算公式为：

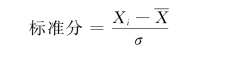
式中，Xi为变量数列中的原始变量值，经过计算后转换成了标准分。标准分实际上是将不同均值和标准差的总体都转换为均值为0、标准差为1的总体，将各个个体的数据转换为其在总体中的相对位置，也即标准分反映各单位变量值以平均数为中心的相对位置。标准分不改变原变量值大小的位序，不仅表明各单位标志值在总体分布中的地位，还能用于不同分布原始数据的比较。

例如，某班学生先后进行了两次难度不同的统计学考试，第一次考试成绩的均值和标准差分别为80分和10分，第二次考试成绩的均值和标准差分别为70分和7分。李某第一、第二次考试的成绩分别为92分和80分，那么就李某与全班相比较而言，她哪一次考试的成绩更好呢？

所以，可认为就与全班相比而言，李某第二次考试的成绩更好一些。

由上例可见，标准分的比较只有相对意义，没有绝对意义。

标准差除了上述两种应用之外，还有一种更重要的作用，即在抽样推断时计算抽样误差。抽样误差是所有样本指标的标准差，具体计算方法将在本书第六章中介绍。