（一）四分位差的概念

把一个变量数列分为四等分，形成三个分割点（Q1、Q2、Q3），这三个分割点的数值就称为四分位数。其中第二个四分位数Q2就是中位数Me。

四分位差就是第三个四分位数Q3与第一个四分位数Q1之差，用Q.D.表示四分位差，用公式表示，即

（二）四分位差的计算

1.根据未分组资料求Q.D.。

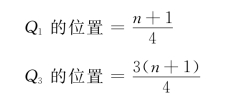
式中，n为变量值的项数。

例如，某数学补习小组11人的年龄（岁）分别为：17，19，22，24，25，28，34，35，36，37，38

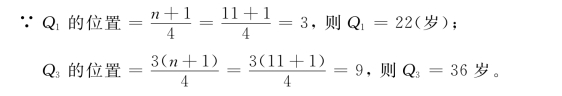
∴四分位差Q.D.=Q3-Q1=36-22=14（岁）。

计算结果表明，该小组有一半人的年龄集中在22～36岁之间，且他们之间的最大差异为14岁。

2.根据分组资料求Q.D.。

其步骤是：(www.daowen.com)

①确定Q1与Q3的位置：

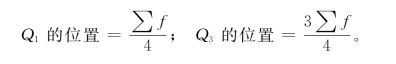
②求向上累计次数，在累计次数中找Q1与Q3所在组。若是单项数列，则Q1与Q3所在组的标志值就是Q1与Q3的数值；若是组距数列，确定了Q1与Q3所在组后，还要用以下公式求近似值

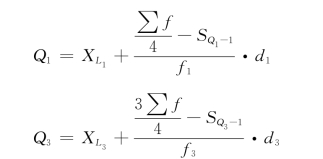
式中，XL1，XL3——分别为Q1与Q3所在组的下限；

f1，f3——分别为Q1与Q3所在组的次数；

d1，d3——分别为Q1与Q3所在组的组距；

SQ1-1，SQ3-1——分别为Q1与Q3所在组以前一组的累计次数；

∑f——为总次数。

现仍用前述表3-18资料，说明其计算方法：

计算结果表明有一半工人的日产量分布在72.40～92.96千克之间，且它们之间的最大差异为20.56千克。

由此可见，四分位差不受两端各25%数值的影响，因而能对开口组数列的差异程度进行测定；尤其是当用中位数来测度数据集中趋势时，对应的离散程度就特别适合用四分位差来描述。但四分位差不反映所有标志值的差异程度，它所描述的只是次数分配中一半的离差，所以类同全距，四分位差也是一个比较粗略的指标。