编制组距数列牵涉的问题较多,不仅取决于分组标志的选择,而且要看分组界限的确定是否合理。在编制过程中,要正确处理以下三个具体问题:
(一)组距和组数
在组距数列中是用变量变动的一定范围代表一个组,每个组的最大值为组的上限,最小值为组的下限。每个组上限和下限之间的距离称为组距。
编制组距数列必须要确定组距和组数。首先要找出全部变量的最大值和最小值的距离(即全距),以及大多数变量集中在什么范围内,然后才能据以考虑组距和组数的问题,务必使分组的结果尽可能反映出总体分布的特点。
组数的确定和组距有密切联系。组距大则组数少,组距小则组数就多,两者成反比例的变化。在具体确定组距时,应使组距能体现组内资料的同质性和组与组资料的差异性。
89-88 76-99 74-60 82-60 89-86
93-99 94-82 77-79 97-78 95-92
87-84 79-65 98-67 59-72 84-85
56-81 77-73 65-66 83-63 79-70
将上述资料按数值大小排列如下:
56-59 60-60 63-65 65-66 67-70
72-73 74-76 77-77 78-79 79-79
81-82 82-83 84-84 85-86 87-88
89-89 92-93 94-95 97-98 99-99
经初步加工,大致可看出资料的集中趋势。资料的最小值为56分,最大值为99分,则全距=99-56=43分,即数列中最大值与最小值之差。根据考试成绩性质的不同,在60分的数量界限的基础上分为不及格、及格、中等、良好、优秀五个类型,并将每组组距定为10分,编制如下(见表2-9所示)组距数列,则基本上能准确反映学生成绩的分布特征。
表2-9 某班学生统计学考试成绩表
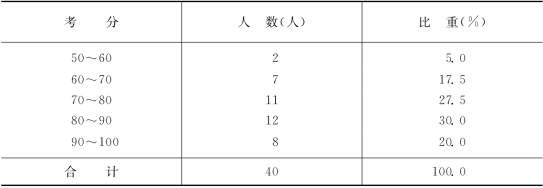
本例视研究对象本身的特点和研究的目的,按组距为10,定组数为5。按经验的看法,组数过多或过少都不妥,一般情况下可分5~7组,组数尽可能取奇数,避免偶数。
(二)等距分组和异距分组
组距数列根据组距是否相等,分为等距数列和异距数列两种。等距数列中各组组距都是相等的(如表2-9所示);异距数列中每组的组距是不等的(如表2-10所示)。
表2-10 某地区人口分布状况

1.等距数列。等距数列分组时,一般应依据总体内部情况的定性分析来确定组数,然后用全距除以组数,确定组距,并据以划分各组的界限。
设R为全距、K为组数、i为等组距
如上例,R=43,设K=5
![]()
为计算方便,i宜取5或10的整数倍,故可令i=10。根据考分现象可知,60分是必须划分及格与不及格两种性质的数量界限,因此,可在60分以上及以下均按10分的等组距进行分组。
按表2-9资料可画成直方图(见图2-2所示)。
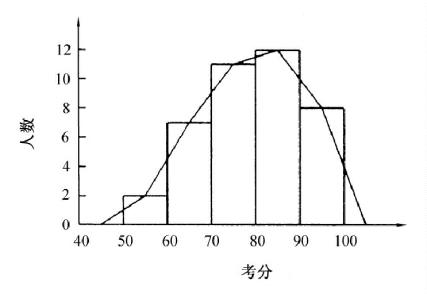
图2-2 某班学生统计学考试成绩次数分配曲线图(https://www.daowen.com)
在直方图的基础上,用直线连接各条形顶边的中点(即各组的中值点),形成一条曲线(折线),曲线两端应在直方图的左右两边各延伸一个假想组,并将次数曲线两端连接横轴两端假想组中点,就形成了次数分配曲线(折线)图,这种直方图的总面积恰等于曲线所覆盖的全部面积。
等距数列适用于标志变异比较均匀的现象,或者说,各组性质差异是由变量值均匀增加或减少而引起的。例如,学生成绩60分以上者,每增加10分就进入高一级档次。人口按身长、体重的分组等,一般均采用等距数列。
2.异距数列。在异距数列中各组次数的数值受组距不同的影响。在研究各组次数实际分布时,要消除组距不同的影响,这就要将不等组距的次数换算为标准组距次数。可以数列中最小组组距为标准组距,将不等组距次数换算为统一的标准组距次数,并依此绘制图形,或者是在原数列基础上先计算次数密度或频率密度,其公式为

再根据次数密度或频率密度来绘制图形。以上两种方法实质上是一样的。现以某厂工人年龄分布情况为例,将这两种方法的换算结果列成表2-11。
表2-11 某公司职工年龄分布情况
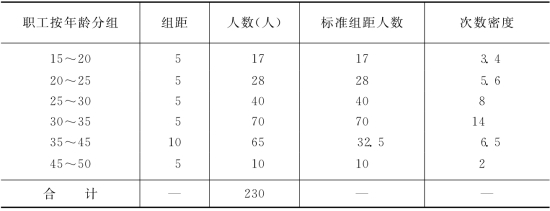
以上标准组距最后两组的人数为32.5与10,实际上也就是次数密度乘以最小组距5的结果。现根据上述数列的换算资料绘制次数分配曲线(如图2-3所示)。
从图2-3可见,按标准组距人数或次数密度绘制的次数分配曲线消除了由于不等组距所造成的影响。由于第五组组距(35~45)大于第四组,图中三角形a<a′,这样,直方图的面积略小于次数分配下的曲线面积。
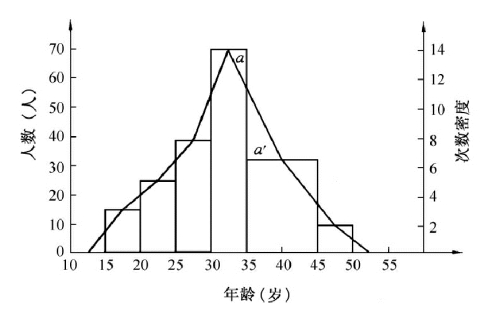
图2-3 某公司职工年龄次数分配曲线图
异距数列常在以下场合运用:第一,有许多社会经济现象的分布存在明显的偏斜状况,这时变量不适合等距分组,必须采用异距分组。例如,人口总体的年龄分布,考虑到80岁以上的高寿者在总人口中所占比重极小,故分组时80岁以下可按10岁组距分组,80岁以上的组距就应扩大。第二,有些社会经济现象的标志变异范围较大,其变量若按一定比例关系变化发展的话,可按等比间隔分组编制异距数列。例如,钢铁厂高炉按容积(m3)的异距分组为:100以下,100~200,200~400,400~800,800~1-600,1-600以上。显然,其组距间隔等比为2。
(三)组限和组中值
1.组限。确定组距和组数之后,还有确定组限的问题。组距两端的数值称组限。组距的上限、下限都齐全的叫闭口组;有上限缺下限,或有下限缺上限的叫开口组。
确定组限要遵守一个基本原则,即按这样的组限分组后,标志值在各组的变动能反映事物的质的变化。也就是要使同质的单位在同一组内。这就涉及组限的表示方法,下面介绍两种常用的表示方法。
(1)按连续变量分组,由于相邻两组的上限与下限通常以同一个数值来表示,每一组的上限同时是下一组的下限,为了避免计算总体单位分配数值的混乱,一般原则是把到达上限值的单位数计入下一组内,即称为“上组限不在内”原则。如前例50~60分,满了60分,应计入下一组60~70分这一组内。这样做,不仅能使计算方法统一,而且这些数字也往往正是事物发生质变的量的界限。就拿60分来说,事实上是成绩及格与不及格的数量界限。
(2)按离散变量分组,则相邻两组的上限与下限通常是以两个确定的不同整数值来表示,故相邻两组的上下限可以不重合。例如,企业按工人数分组可分为以下各组:100人以下,101~300人,301~500人,501~1-000人,1-000人以上,这是一般的表示方法。也可以按“上组限不在内”的原则写为重叠式组限,如上面的工人人数分组,也可写成:100人以下,100~300人,300~500人,500~1-000人,1-000人以上等。
2.组中值。组距数列是按变量的一段区间来分组,掩盖了分布在各组内的单位的实际变量值。为了反映分在各组中个体单位变量值的一般水平,统计工作中往往用组中值来代表它。组中值是各组变量范围的中间数值,通常可以根据各组上限、下限进行简单平均,即
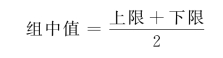
如上例50~60分一组的组中值即为55分。
对于开口组组中值的确定,一般以其相邻组的组距的一半来调整:

例如,按完成净产值分组(万元):
10以下
10~20
20~30
30~40
40~70
70以上
则:
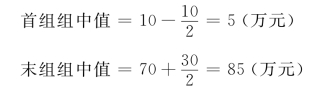
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。





