完全积累制下，一代人工作期间的缴款进入基金账户积累，用来支付这一代人退休后的养老金。“世代1”（G1w）工作并缴款，但不领取补助。这些缴款在一项信托基金中积累起来，投资于资本市场，所产生的收益（包括基金盈余产生的利息）被用来在“年代2”中当“世代1”（G1R）退休时向其支付补助。已经在“年代1”退休的“世代0”（G0R）在该项目开始后将得不到补助，他们必须依靠自己的积蓄或者购买商业养老保险（参见图3-10）。

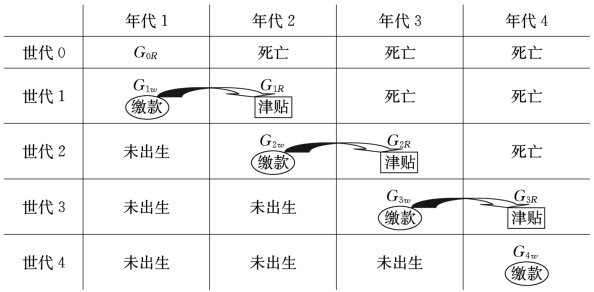
图3-10　完全积累式（基金式）养老保险模式

资料来源：同图3-9。

在完全积累制下，在t-1期就业人口中的每一个人根据一定的比例C从工资中扣除养老金进行积累，基金投资于证券或债券市场，当他们在t期退休时，根据金融市场的资本报酬率即市场利率r获得养老金给付，因此t期的养老金由下式决定：⑩

bt=（1＋r）·C·wt-1　（3-18）

Nt=N0（1＋n）t　（3-19）

其中，δ为资本折旧率。(www.daowen.com)

索洛（Solow）在其增长模型中推导出著名的经济增长的黄金定律：当一个经济的资本的增长率等于劳动力增长率加上劳动生产率的增长率时，经济处于最优增长的路径，与此相应的利率即为长期动态的最优利率。

当经济一旦处于索洛所描述的黄金增长路径时，该经济中资本的增长必须保持这样的关系：资本的边际报酬率（即利率r）减去资本折旧率δ之后等于人口增长率和劳动生产率的增长率。因此，在经济处于黄金增长路径时，资本市场所能获得的毛利率应该为：

r=n＋λ＋δ　（3-21）

净利润应该为：

rnet=n＋λ　（3-22）

将上式中的净利率代入式（3-18），有：

bt=（1＋n＋λ）·C·wt-1　（3-23）

式（3-23）和式（3-17）相同，因此，养老保险体系无论是采用现收现付制，还是采用完全积累制，只要在这两种养老体系下，一个经济的最优储蓄率能够得到保证，养老金增长的物质基础是完全一样的，即养老金获得增长的物质源泉只能是下一代就业人口的增长和他们的劳动生产率的提高。