所谓预测误差,是指统计数据实际值与预测值之间的离差。一般用![]() 表示,yt为实际值,
表示,yt为实际值,![]() 为预测值。为了比较预测方法的精度,需要测定一系列的预测误差,综合反映预测误差的大小。反映预测误差的综合指标有平均误差、平均绝对误差、均方误差和均方根误差4 种。
为预测值。为了比较预测方法的精度,需要测定一系列的预测误差,综合反映预测误差的大小。反映预测误差的综合指标有平均误差、平均绝对误差、均方误差和均方根误差4 种。
1.平均误差![]()
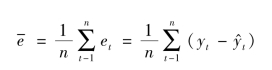
平均误差是预测误差的简单平均,预测误差的数学期望值等于0。如果![]() ≠0,表明预测存在偏误,其绝对值越大,偏误越大。当
≠0,表明预测存在偏误,其绝对值越大,偏误越大。当![]() >0,为正偏误;当
>0,为正偏误;当![]() <0,为负偏误;当
<0,为负偏误;当![]() =0,表明预测效果较好。
=0,表明预测效果较好。
2.平均绝对误差(MAE)
由于预测误差有正有负,为避免正负抵消,确切反映离差的大小,解决的方法是取绝对值,计算平均绝对误差,其计算公式为:
平均绝对误差:
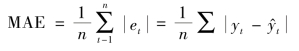
3.均方误差(MSE)
均方误差是预测误差平方和的平均数,其计算公式为:
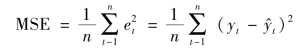 (www.daowen.com)
(www.daowen.com)
4.均方根误差(RMSE)
均方根误差是均方误差的平方根,其计算公式为:
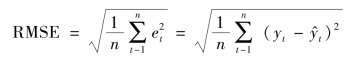
以上4 种指标均可综合测定误差的大小和评价模型、方法的优劣。均方根误差还可用于对预测误差的控制。在实际中,应用最广泛的是均方根误差(又称估计标准误差),其作用与标准差相似,不同的是这里的离差不是以变量值与一个平均数为中心计算的,而是以变量值与其对应的预测值为中心计算的。标准差反映的是平均数的代表性大小,而均方根误差则是表示一条平均数线的代表性大小。一般来讲,指标数值越小,误差越小,预测精度越高。具有最小误差的方法最优,模型最好,承担的风险最小。
【例9-15】 现以9.4 节表9-8 的有关资料及所建立的预测方程求得的各期预测值(又称理论值)为例,说明均方根误差的计算,如表9-13 所示。
表9-13 预测误差计算表
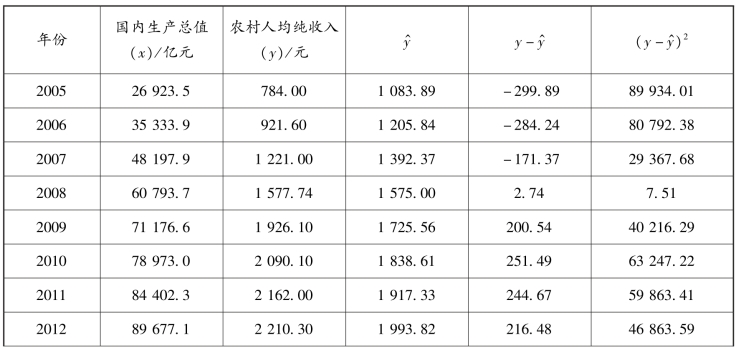
续表

解:根据Excel 统计功能,列表计算相关系数r、回归参数a(截距)、回归系数b。具体方法:打开Excel 单击工作栏中的fx按钮,单击“统计”中的“CORREL”“INTERCEPT”和“LINEST”选项,并按提示选定变量y 和x 值列,即可计算出所需结果。方程式为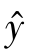 =693.50 +0.014 5x,也可根据公式计算。将表9-13 中的资料代入公式,得均方根误差:
=693.50 +0.014 5x,也可根据公式计算。将表9-13 中的资料代入公式,得均方根误差:
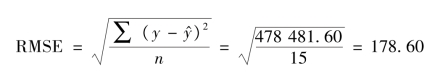
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







