1.多元线性回归模型

一个现象在数量上的变化，往往是由于多种因素综合作用的结果。例如，农作物收获量除了受化肥施用量影响之外，还受土壤条件、气候状况、水利条件、种子等多种因素的影响。在一元线性回归分析中，我们没有将这些因素对自变量的影响考虑在内。许多情况下，为了更准确、完善地分析变量之间的相互关系，应将影响因变量在数量上发生变化的主要因素列入研究的范围。在统计中，分析一个因变量与多个自变量之间相互关系的理论和方法称为多元回归分析。这里我们仅介绍二元线性回归模型，掌握了二元线性回归，多元线性回归也就不难掌握了。

二元线性回归模型如下：

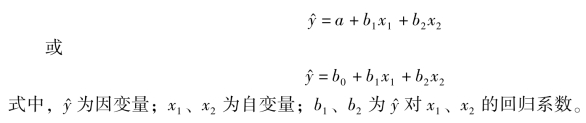
确定参数a、b1、b2的数值，仍然用最小二乘法来估计，根据最小二乘法的原理可以求得如下的标准方程：

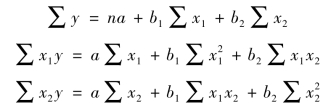
或

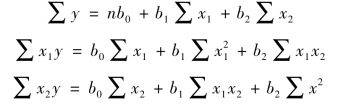
通过对标准方程求解，可得到a、b1、b2的数值，将其代入回归方程，即可得到二元回归方程。

【例9-14】　设某地区卫生陶瓷需求量（y）与城镇竣工住宅面积（x1）、医疗卫生机构建筑面积（x2）存在密切的复相关关系（其统计资料见表9-11）。

表9-11　某地区卫生陶瓷需求量相关资料

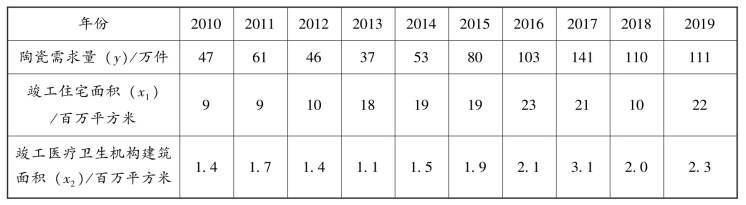
要求：建立二元线性回归方程，用最小二乘法求估计参数，并预测当竣工的城镇住宅面积为2 600 万平方米、医疗卫生建筑面积为250 万平方米时的卫生陶瓷需求量。

解：设二元线性回归方程为：

（1）建立标准方程组。

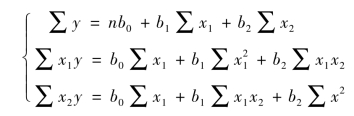
（2）根据表9-12 中的已知资料按标准方程组的要求计算相关数据。

表9-12　已知资料

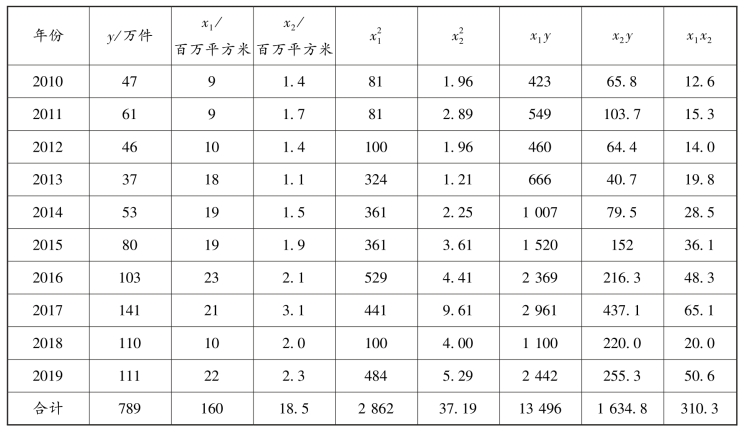
将表中数据带入方程组，得：

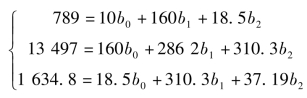(www.daowen.com)

根据行列式求解：b0＝-31.242 5，b1＝0.121 28，b2＝58.487 6。则二元线性回归方程为：

当x1＝26，x2＝2.5 时有：

即陶瓷需求量为118.13 万件。

2.非线性回归模型

前面所述的线性回归，是指自变量同因变量之间的变化有等量增加（或减少）的趋势，其变化关系呈回归线性关系。在现实经济生活中，自变量对因变量的影响并非都是线性关系。如商品销售量的变动并不随着相关因素的变化按等差级数增减，许多情况下，还会按等比级数增减。这种趋势变动线就不是直线，而是曲线。这时，就要采用非线性回归预测模型进行预测。在建立曲线回归方程时，首先必须确定变量之间关系的类型。可根据观察资料进行分析比较，特别是通过相关图，观察图像散点分布情况，结合一些已知函数的图形，选择适当的数学表达式作为回归模型。确定非线性回归参数的一般方法：对其中某个变量做某种变换，使新变量对另一变量有线性关系。即通过某种变换使非线性回归转化为线性回归，然后按拟合成的线性回归方程求出参数，再建立数学模型进行预测。下面介绍几种常见的非线性回归模型及其相应的线性变换公式，以供参考。

（1）抛物线。

假设x1＝x，x2＝x2，…，xn＝xn，则上式可化为x1，x2，…，xn为自变量的多元线性回归模型：

可用最小二乘法求解，求得参数a，b1，b2，…，bn。

（2）幂函数曲线。

这是一个直线方程，可用最小二乘法求出a′，b，再计算出a 的值。

（3）指数函数曲线。

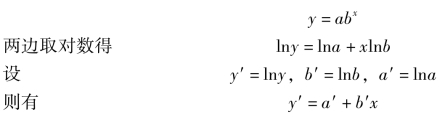
这是一个直线方程，可用最小平方法求出a′，b′，再计算出a 和b 的值。

（4）S 形曲线。

这是一个直线方程，可用最小二乘求出a，b。