分割平均预测法是估计模型参数值最简单的方法之一。其要求是，时间序列的实际水平与理论水平离差总和必须等于零。它既可用于配合直线方程，也可配合曲线方程。其方法是，如果时间序列为直线型（各期的逐期增长量大体相同），原时间序列是偶数项时，进行等分（若是奇数项，则删去首项后等分），再分别求出各部分的平均数作为直线上的两点，代入联立直线方程式求解，得到直线趋势方程，最后用以预测；如果时间序列属抛物线型（各期的二级增长量大体相同），由于抛物线有3 个参数，则须将原序列分为首、中、尾相等的三部分，然后由各部分求出的平均数作为抛物线的3 个点，代入抛物线方程求解，得到抛物线方程，用以预测；如果时间序列属指数曲线型（各期的增长速度大体相等），仍将原数列分为相等的两部分求平均，然后将指数曲线化为对数直线求解即可。

对直线型趋势模型＝a ＋bt（t 为时间序号），参数a、b 由下面方程组求得：

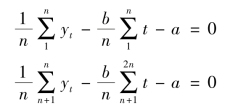
将t 和y 的实际数值代入上式，即求得参数a、b，配合一条直线方程，用以外推预测。

【例9-12】　现以A 国历年粮食产量为例，见表9-8，预测2020 年产量。

解：列表计算（表9-8）。

根据表中数据，从逐期增长量Δy 检查，产量的增长量各期大体相同，所以确定变化趋势为直线型。(www.daowen.com)

表9-8　A 国粮食产量预测计算表　单位：万吨

将表中数据分为相等的两部分，代入联立方程组，求得α＝49 684.572，b＝-363.764。则配合直线的模型为：

将各年的年次分别代入模型，即得各年趋势值（预测产量即表中第4 栏），将各年实际产量减去预测值，即得误差（表中第5 栏），其误差总和等于0。

若预测2020 年的趋势值，即将t＝12 代入模型得：