指数修匀预测法(Modified Moving Average Forecast)又称指数平滑法,是从移动平均法基础上发展形成的一种指数加权移动平均预测法,是一种特殊的指数加权法。它利用本期预测值和实际数值资料,以平滑常数α 为加权因子来计算指数平滑平均数。指数修匀预测就是以此平滑平均数为下期的预测值。其公式为:
![]()
式中,α 代表平滑常数(或修匀常数)(0≤α≤1);![]() 为下期预测值;
为下期预测值;![]() 为本期预测值;yt为本期实际值。
为本期预测值;yt为本期实际值。
α 值是一个经验数据,它的大小体现了不同时期数值在预测中所起的不同作用:α 取值大,表明近期数值的倾向性变动影响大,适应新水平敏感;α 取值小,表明近期数值的倾向性变动影响小,越趋于平滑,越能反映趋势。一般的取值规律:若重视近期数值的作用,可取大值,如0.9、0.8、0.7 等;重视平滑趋势可取小值,如0.1、0.2、0.3 等,有时也可取0.5。
【例9-10】 现以某商场月销售额为例,用指数修匀法预测如下(表9-6)。
解:列表计算如下。
表9-6 某商场月销售额预测表
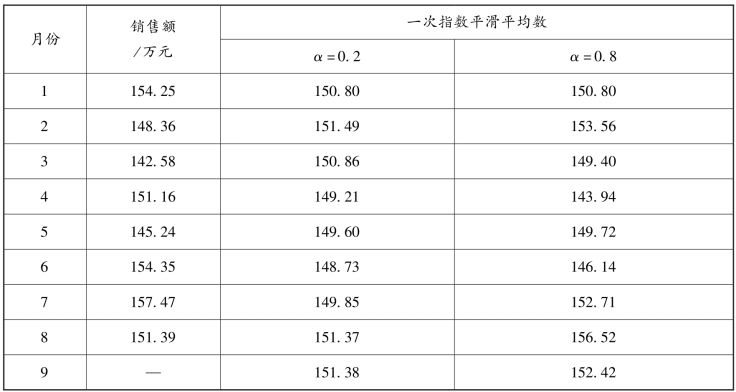
设已知1 月份预测值为150.8 万元。α 取0.2 和0.8,其预测计算见表9-6。在计算中没有初始预测值时,可用实际值来代替。
在预测中可选几个α 值进行计算,然后进行筛选,取其最适宜的指数平滑平均数为预测值。(https://www.daowen.com)
应注意,指数平滑有一次、二次与三次之别。在没有明显的长期趋势资料中,使用一次平滑即可;存在着直线趋势时,则使用二次平滑,即对一次指数平滑再进行一次指数平滑。这是因为,无论时间序列呈上升或下降趋势,一次指数平滑平均数总滞后于实际值。当实际趋势下降时,预测值高于实际数;当实际趋势上升时,预测值低于实际数。为了降低滞后误差,可用二次指数平滑法加以修正。其公式为:

在建立预测公式时,还要分析时间序列的发展趋势是直线型还是非直线型。如果为直线型,可采用下面的直线模型据以预测。
![]()
式中,at、bt为平滑系数;yt+T为第t +T 期的预测数;T 是要提前的预测期数。at、bt计算公式如下:

可见,二次指数平滑值一般都不直接用于预测,而是为了求平滑系数,建立线性时间模型来预测,以便修正指数平滑值的滞后现象。
另外,当存在曲线趋势时,则要使用三次指数平滑法,即将二次指数平滑值再做一次指数平滑,求得三次指数平滑值。三次指数平滑值也不直接用于预测,而是为了求平滑系数,以便建立二次曲线模型。
三次指数平滑法的基本公式是:
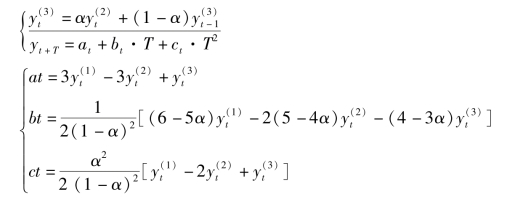
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。








