插值推算法是根据动态数列和变量数列的若干已知对应数值推算其数列未来趋势的对应数值。插值推算法主要有下面几种。

1.比例推算法（利用平均发展速度推算）

比例推算法是在本期实际值的基础上，乘以一定历史时期的平均发展速度，即可得出下期的预测值。其公式为：

式中，yt为本期实际值；为t ＋k 期的预测值；为一定时期的平均发展速度；k 为距本期（t 期）的时期数；t 为本期。

【例9-6】　某市2010—2019 年生产总值资料见表9-2。试预测该市2020 年生产总值。

表9-2　某市2010—2019 年生产总值资料　单位：万元

解：2020 年生产总值为：

2.线性插值法（Linear Interpolation Method）

前面所讲的比例推算法只是根据一个地区（单位等）的比例关系估算类似地区（单位等）的数值。但是一个地区（单位）的比例关系并不普遍适用于其他地区（单位）。如果掌握了各不相同的若干地区（单位）的比例关系，则要考虑这些比值之间的关系，就不能只用一个地区（单位）的比例关系来估算。线性插值法是根据已掌握的两项有关实际资料来推算第三项对应的未知资料。根据这两点只能确定唯一的一个直线方程，即：

【例9-7】　某贸易公司所属5 个食品厂2019 年某产品的生产量及生产费用资料见表9-3。该公司另有一个生产240 吨的食品加工厂，由于生产费用资料不全，不能及时汇总。要求：①按甲厂资料推算该食品厂的生产费用。②按甲、戊两厂资料推算240 吨食品加工厂的生产费用。

表9-3　2019 年某产品生产量及生产费用资料表(www.daowen.com)

解：（1）按甲厂资料推算该食品厂生产费用。

（2）按甲、戊两厂资料推算该厂生产费用。

如果对线性插值多项式做简单变换，则可得拉格朗日插值法（Lagrange Interpolation Method），即掌握了两个以上实际对应资料，以此来推算某项对应的未知资料。它是线性插值法的推广。

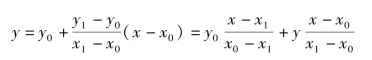
则拉格朗日多项式为：

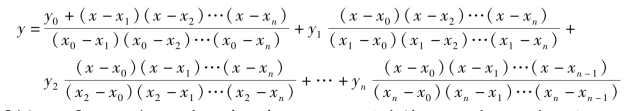
【例9-8】　设某工业部门有如表9-4 所示的资料，问该部门投资额为2 000 万元时，其产量是多少？

解：根据拉格朗日插值公式得

即当投资额为2 000 万元时，产量为23.67 千吨。

表9-4　某工业部门投资额及产量资料