若回归模型表现为曲线形式，则这就是曲线回归分析，曲线模型种类多样，不过在统计研究中常用的曲线模型主要有以下几个。

在建立曲线回归方程时，最重要的问题是选择合适的曲线类型，解决这个问题，主要是通过作图，然后凭借经验从图形显示的曲线形状来判断应当拟合的曲线。

图8-6 至图8-8 给出了以上三种曲线的图形。

在大多数情况下，曲线回归问题可以通过变量的变换，将其转化成线性回归问题，然后再用前面介绍的线性回归的方法来解决。

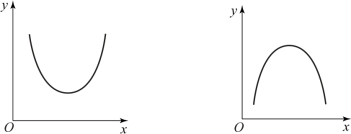
图8-6　二次抛物线

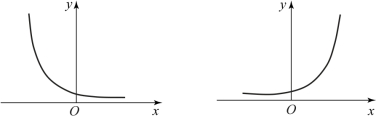
图8-7　指数曲线

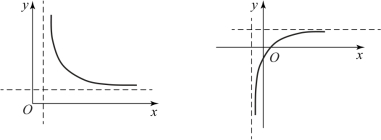
图8-8　双曲线

1.双曲线回归

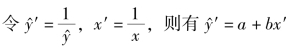
【例8-9】　已知两个变量的数据（表8-15），试建立这两个变量的回归方程。

表8-15　两个变量的数据

做出散点图，如图8-9 所示。

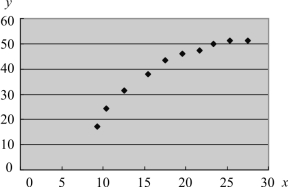
图8-9　散点图(www.daowen.com)

从图8-9 中可以看出这两个变量之间的变动关系基本上是一个递增的双曲线，则用双曲线模型去分析两个变量的关系。计算表见表8-16。

表8-16　x 和y 双曲线回归方程计算表

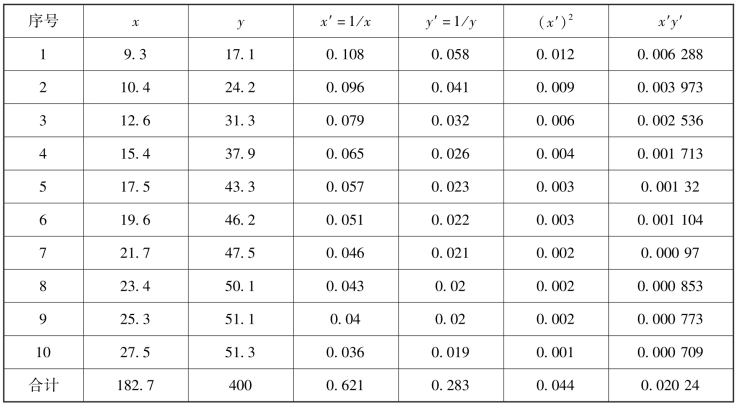
将表中数据代入以下公式：

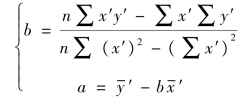
得：

于是有：

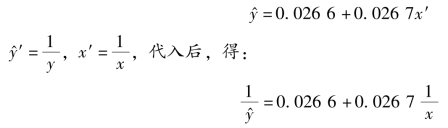
在实际操作中，一元曲线回归不用手工来完成，都是先将数据进行变换，再按照线性回归添加趋势线的方法来拟合曲线。

2.指数曲线回归和抛物线回归

（1）指数曲线方程为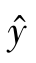＝abx。

两边取对数：ln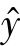＝lna ＋xlnb

令：A＝lna，B＝lnb，则得到一元线性回归模型：

（2）二次抛物线方程为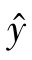＝a ＋b1x1＋b2x2。

令x1＝x，x2＝x2，原方程转化为二元线性回归模型：