在回归分析中,如果变量之间的回归模型是直线方程,则这类回归分析为线性回归分析(直线回归),该直线方程称为线性回归方程。具体地,如果直线方程中只有一个自变量和一个因变量,就称为简单线性回归分析;若存在一组自变量和多个因变量,就称为多元线性回归分析。
1.简单线性回归分析
简单线性回归分析的主要任务是在唯一的自变量x 和因变量y 之间建立一个直线函数,其表现形式为:
![]()
需要指出的是,x 是自变量,![]() 是因变量的y 的估计值,又称理论值。实际观测值y 和理论值
是因变量的y 的估计值,又称理论值。实际观测值y 和理论值![]() 的关系:
的关系:![]() 式中ε 称为离差,反映了因各种偶然因素、观察误差及被忽略的其他影响因素带来的随机误差。因此,用以下方程来表示简单线性回归方程的模型:
式中ε 称为离差,反映了因各种偶然因素、观察误差及被忽略的其他影响因素带来的随机误差。因此,用以下方程来表示简单线性回归方程的模型:
![]()
(1)一般简单线性回归方程。确定![]() =a +bx,主要是确定a 和b,那么如何选择最为满意的a 和b 呢?统计学中有最小二乘法、最大似然法等。其中最大似然法更适用于长期对事物、现象的估计和预测,故常用的是最小二乘法。
=a +bx,主要是确定a 和b,那么如何选择最为满意的a 和b 呢?统计学中有最小二乘法、最大似然法等。其中最大似然法更适用于长期对事物、现象的估计和预测,故常用的是最小二乘法。
最小二乘法的基本思想是让![]() =最小值,又称最小平方法。其原理即拟合一条最佳配置线,使得样本数据点到该直线上对应点的纵向距离和最短,也就是因变量y 的观测值yi与估计值
=最小值,又称最小平方法。其原理即拟合一条最佳配置线,使得样本数据点到该直线上对应点的纵向距离和最短,也就是因变量y 的观测值yi与估计值![]() 的差的平方和达到最小,并据此求得参数a 和b。
的差的平方和达到最小,并据此求得参数a 和b。
将![]() 根据微分求极值的原理,分别对a 和b 求偏导,令其为零。
根据微分求极值的原理,分别对a 和b 求偏导,令其为零。
得:


【例8-6】 根据【例8-1】 中的数据,建立月产量x 和单位产品成本y 之间的直线方程。并估计当月产量x=10(千件)时单位产品成本的数值,见表8-12。
表8-12 直线回归方程计算表
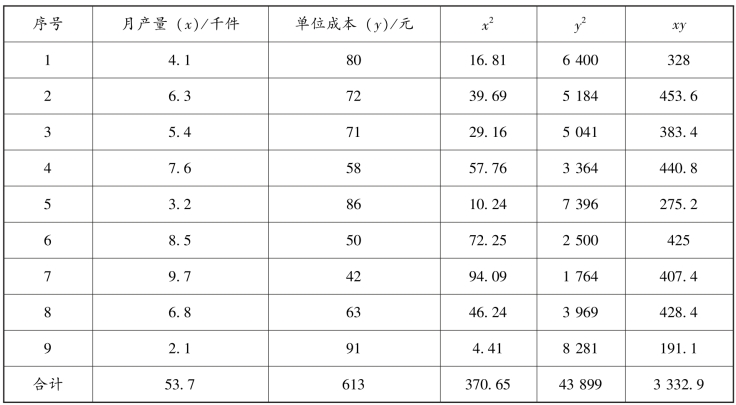
将表8-12 的有关数据代入式(8-8),得:

(2)当时间为解释变量时的简单线性回归方程。若自变量为时间,则用t 表示,此时,直线方程为![]() =a +bt。
=a +bt。

图8-5 月产量和单位成本的线性回归方程
由最小二乘法原理可得:

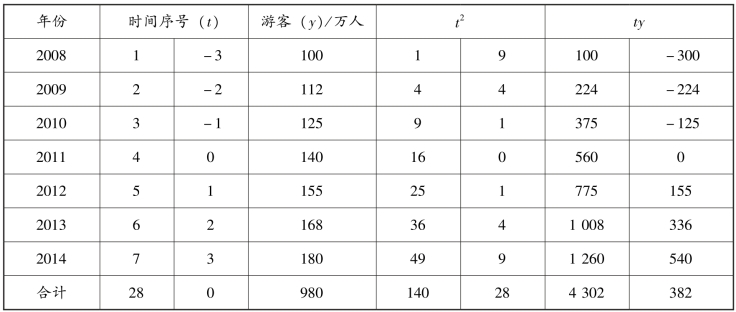
【例8-7】 某游览点历年观光游客的数量见表8-13,用最小二乘法建立直线方程,并预测2020 年的游客数量。
表8-13 游览点观光游客的数量(https://www.daowen.com)
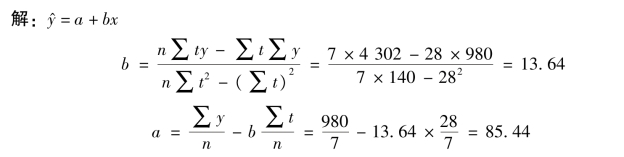
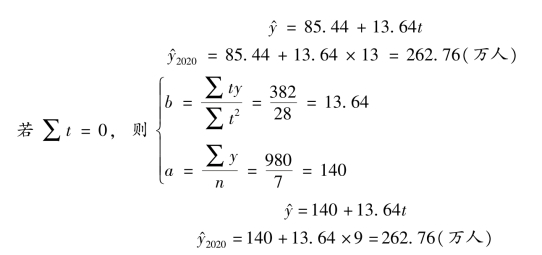
2.多元线性回归分析
简单线性回归反映的是一个自变量和一个因变量之间的关系,但是客观事物非常复杂,许多现象的变动牵扯多个影响因素。例如,一个企业的利润,受产值、成本、价格等多个因素的影响;再如,粮食产量受施肥量,同时也受温度、播种量、土壤的酸碱性、降雨量的影响。所以在现实中,经常要进行一个变量和多个自变量的多元线性回归分析。
其一般形式为:
![]()
为了叙述方便,本书以二元线性回归为例,建立一个因变量y 和两个自变x1,x2的线性回归关系,方程为:
![]()
利用最小二乘法原理,可建立如下方程组:
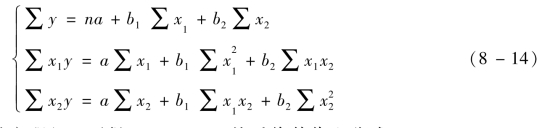
解关于a、b1、b2的方程组,可得a、b1、b2,然后将其代入公式 =a +b1x1+b2x2即可。
=a +b1x1+b2x2即可。
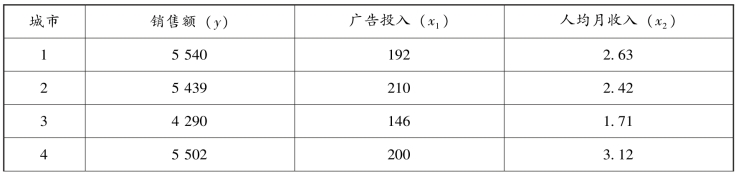
【例8-8】 某服装企业有10 家销售公司分布在不同的城市,决策者通过反复调查分析后认为,影响该企业总销售额的因素为当地的人均月收入和广告投入。经过一年的统计,有关数据见表8-14。
表8-14 企业总销售额与广告投入和人均月收入 单位:千元
续表
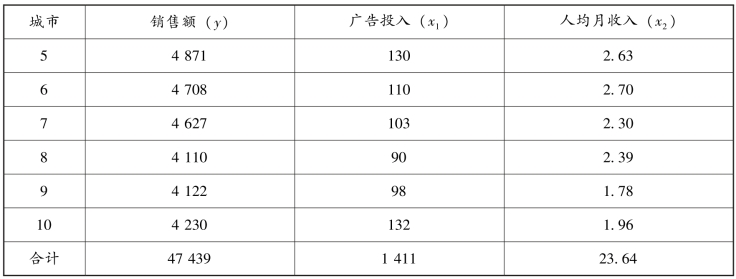
多元线性回归方程也可以按照上述的最小二乘法通过求解方程组得出,但在实际操作中不要求人工计算,可用Excel“数据分析”中的“回归”求解,得出结果如下:
所以方程为:![]() =2 116.52 +8.58x1+599.45x2
=2 116.52 +8.58x1+599.45x2
如果广告投入x1=300(千元),人均月收入x2=2.03(千元),则销售额的估计值为![]() =5 907.4(千元)。
=5 907.4(千元)。
上面的方法可以推广到n 个自变量的情况,对回归方程:
![]()
同样可用最小二乘法,建立一个(n +1)×n 阶方程组,解该方程组可求出有关参数。
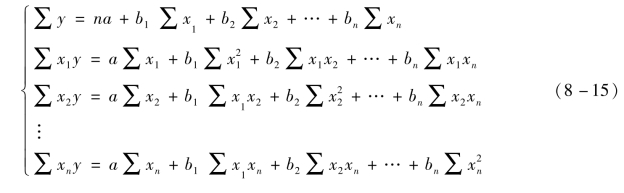
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






