通过前述相关表和相关图，我们仅可以对变量间的相关关系做出一般性的判断，这只是相关分析的开始。如果要想进一步分析变量间的密切程度，就必须用相关系数来衡量和判断。现实中，现象之间一般存在着直线和曲线两种相关关系，而且多为直线相关，这就决定了直线相关分析在实际中也最为常用。这里仅介绍直线相关系数的计算问题。

1.相关系数的含义

相关系数是指直线相关条件下，说明两种现象之间相关关系密切程度的统计指标，一般用r 表示。1890 年，英国统计学家卡尔·皮尔逊（Karl Pearson）提出了相关系数的公式。

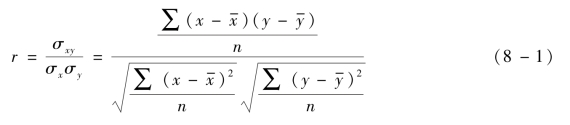
式中，r——相关系数；

σxy——变量x 与变量y 的协方差；

σx——变量x 的标准差；

σy——变量y 的标准差。

需要说明的是，σxy＞0，即为正，说明变量x 与变量y 为正相关；σxy＜0，即为负，说明变量x 与变量y 为负相关（这一点将在稍后说明）。

r 与σxy同符号，且r ＞0 时，变量x 与变量y 为正相关；r ＜0 时，变量x 与变量y 为负相关。

根据相关系数的定义公式可知，相关系数有如下含义：

（1）相关系数的取值范围：-1≤r≤1。因为协方差的绝对值最小为0，最大为σx和σy的乘积。

（2）r 的绝对值越接近于1，表明相关关系越密切；r 的绝对值越接近于0，表明相关关系越不密切。

（3）r＝1 或r＝-1，表明两变量完全相关。

（4）r＝0，表明两变量无直线相关关系。

（5）r ＞0，表明两变量呈正直线相关关系；r ＜0，表明两变量呈负直线相关关系。

实际中，人们经过长期实践，已总结出了一个判别现象间相关密切程度的一般标准，即｜r｜＜0.3，视为无相关；0.3≤｜r｜≤0.5，为低度相关；0.5≤｜r ｜＜0.8，为显著相关（中度相关）；｜r｜≥0.8，为高度相关。

2.相关系数的计算

相关系数的计算根据资料的分组情况，既可采用定义公式，也可采用简捷公式，还可采用其他计算方法。

（1）根据定义公式计算相关系数（未分组资料）。具体计算时，要用相关资料设计一个计算表，先将定义公式中的基本数据计算出来，即先列出5 个计算栏：

【例8-2】　已知某地区社会生产总值和社会商品零售总额的历史资料（表8-5），计算相关系数。

表8-5　某地区社会生产总值和社会商品零售总额资料　单位：亿元

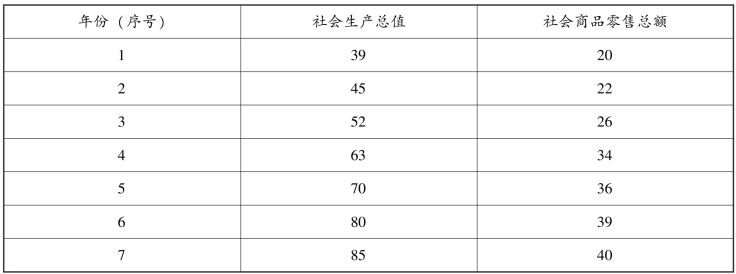
解：列表计算相关资料，见表8-6。

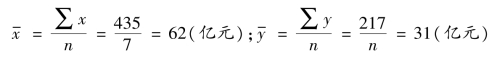
表8-6　相关系数计算表1

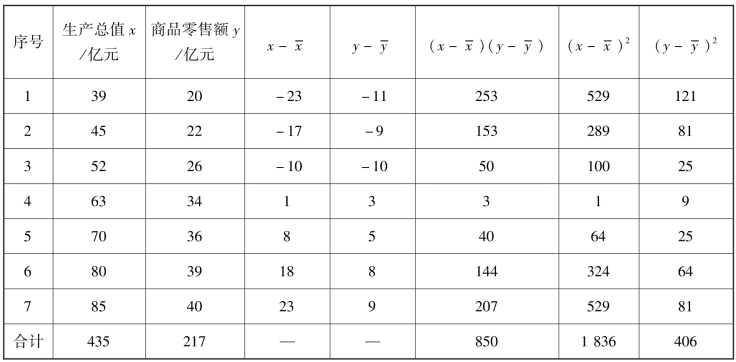
根据表8-6 中的数据计算得：

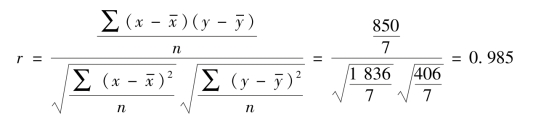
注意：由于定义公式的分子和分母中都有公因子1／n，同时约掉，相关系数的公式可写成：

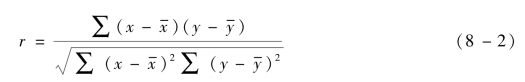
显然，定义公式是通过变量离差乘积之和的平均数来计算相关系数的，所以这个公式又称为积差法公式。

（2）相关系数的简捷计算方法。相关系数的定义公式是根据两变量的离差计算的，当为除不尽的小数时，计算既烦琐又影响准确性，实践中多采用根据定义公式推导出的简捷公式计算相关系数。公式为：

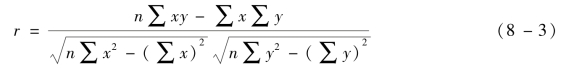
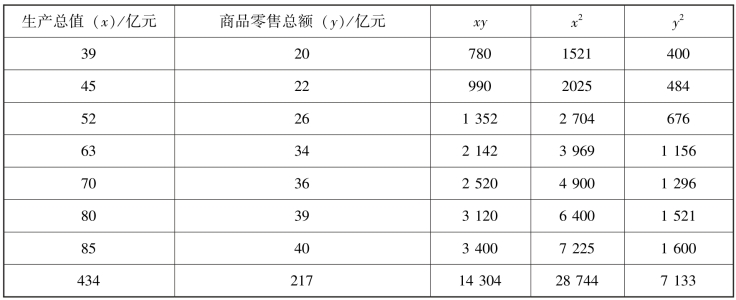
显然，按照这一公式计算相关系数，只需列3 个计算栏：xy、x2、y2，而且避免了平均数、协方差、标准差的直接计算，大大简化了计算过程。现根据表8-5 的资料，用简捷公式计算相关系数（表8-7）。

表8-7　相关系数计算表2

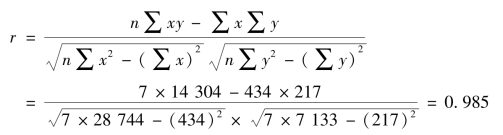
（3）相关系数的其他计算公式。根据定义法公式，还可以推导出相关系数的其他公式。

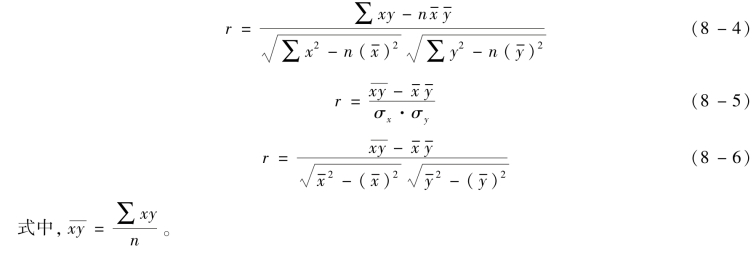
下面举例说明利用双变量分组资料计算相关系数的方法。(www.daowen.com)

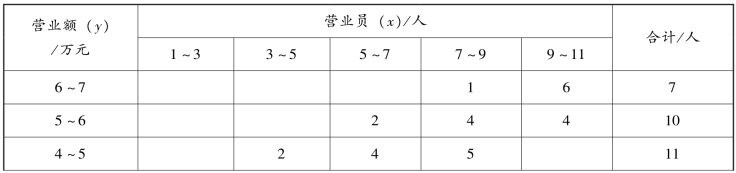
【例8-3】　表8-8 是某地40 家商店的营业员和营业额资料。试根据表中资料求相关系数。

表8-8　双变量分组相关表

续表

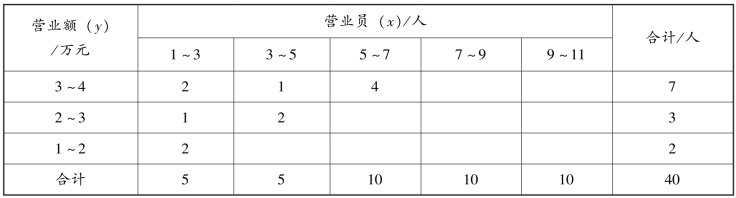
解：根据双变量分组相关表计算相关系数时，x 和y 值均取各分组的组中值，以各组频数加权计算相关系数。先列表计算（表8-9）。

表8-9　加权相关系数计算表

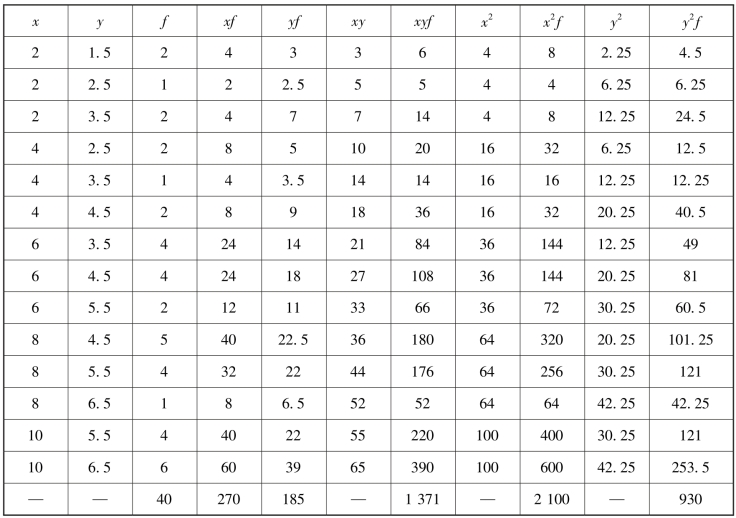
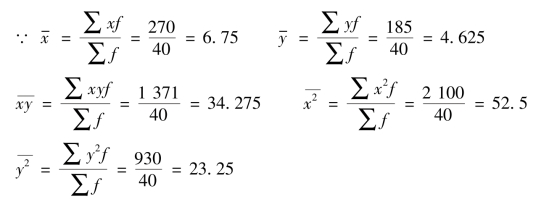
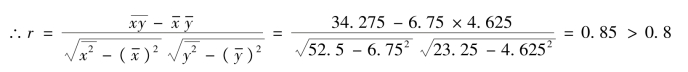
因为，r ＞0.8，所以，该商店营业人员与营业额存在高度正相关关系。

3.相关系数的显著性检验

测算两个变量的相关系数，是从二元总体中随机抽取一个样本，再用样本的相关系数去推断，因为推断误差的存在，不可能保证百分之百可靠。也就是说，因为样本是随机抽取的，根据其计算出的相关系数虽然很大，但总体可能并不具备相关性。那么总体到底有没有线性相关性，在得出结论前，还必须进行假设检验。

检验样本（相关系数为r）是否会来自一个无线性关系的总体（总体的相关系数为ρ），可以采用费舍（

R.

A.Fisher）的t 检验法。

（1）原假设：H0：ρ＝0。备择假设：H1：ρ≠0。

（2）检验统计量为t＝其中n-2 为自由度。

（3）若显著性水平为α，查t 表的临界值为

（4）若则拒绝原假设，接受备择假设，即认为样本的相关系数显著，可以说明总体两个变量间存在着线性相关，检验通过。若｜t｜＜则结论相反。

【例8-4】　根据【例8-1】 中9 家企业的产品月产量和单位成本的样本资料，计算相关系数并对其进行显著性检验（表8-10）。

表8-10　相关系数计算表3

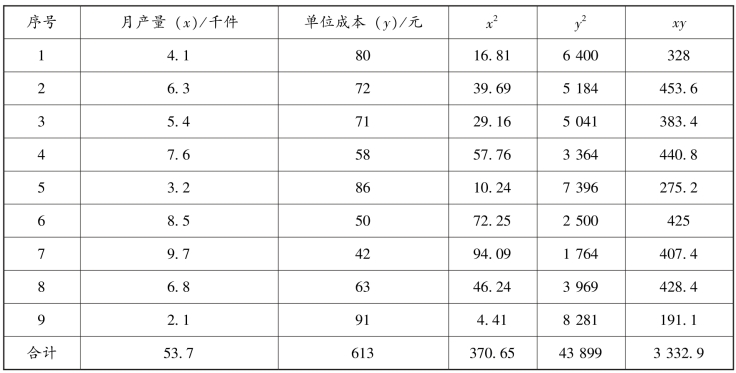
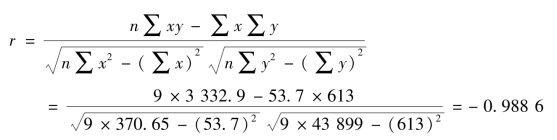
已知：r＝-0.988 6，n＝9，提出如下假设：

H0：ρ＝0；H1：ρ≠0

4.时间数列的自相关

以上我们从静态角度对两个变量的相关关系进行了讨论。但是，相关关系并不仅限于静态，在时间动态方面也可应用相关分析的方法，基本方法与静态的完全相同。比如，时间数列自相关，就是研究一个变量的发展变化对其自身将来的变化所产生的影响。这种现象在经济活动中经常存在，当年的经济状态会对下一年度、下两年度甚至更远的年份产生影响，如已经形成的工业生产水平会影响明年或后年的工业生产水平等。

进行时间数列的自相关分析，需要计算自相关系数，其方法与前面所讲的相关系数在本质上是相同的，公式为

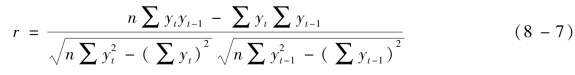
式中，t 代表时间；t-1 是t 期（年）的前一期（年）。

【例8-5】　某地区2009—2019 年的生猪收购量资料见表8-11，试计算自相关系数。

表8-11　时间数列自相关计算表

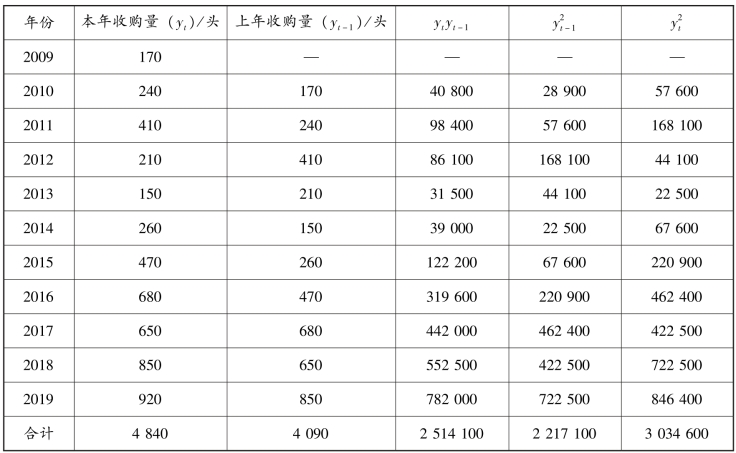
解：将上年收购量与本年收购量一一对应排列见表8-11，则可看出，随着上年收购量yt-1的增长，本年收购量yt也有增长的趋势，可初步判断两者呈正相关关系。

注：∑yt＝4 840 中不包括170。

如果根据各项资料（170，240），（240，410），…，（850，920）绘制相关图，可见本期收购量yt（纵轴）与上期收购量yt-1（横轴）之间的关系大体上接近直线（图略）。因此，通过该资料可计算直线自相关系数。

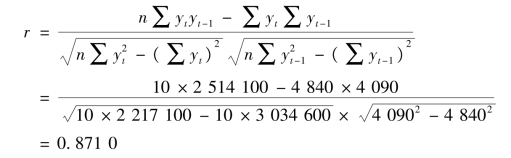
结果说明，本年收购量yt与上年收购量yt-1之间高度相关。