相关分析是对客观社会经济现象间存在的相关关系进行分析研究的一种统计分析法。其目的在于分析现象间所存在的相关关系及对其所表现出的规律性进行数量上的推断和认识，以便为回归分析提供依据。在实际工作中，有非常广泛的应用。相关分析的主要内容和程序如下。

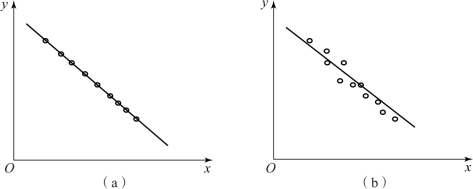
图8-2　相关关系的组合类型

（a）完全线性负相关；（b）不完全线性负相关

1.判别现象间有无相关关系

现象间有无相关关系，这是相关分析的起点和出发点。只有现象间确实存在相关关系，才可能进行相关分析。所以，进行相关分析时，首先要通过定性分析，借助相关表或散点图来判别现象间是否确实存在相关关系，相关关系表现为何种形式就用什么样的方法分析。否则，若把本属于直线相关的变量用曲线的方法来分析，就会产生认识上的偏差，做出错误的判断。

2.判定相关关系的表现形态和密切程度(www.daowen.com)

相关关系是一种数量上不严格的相互关系。只有当变量间确实存在高度密切的相关关系时，才可能进行相关分析，进而对社会经济现象进行预测、推算和决策。因此，判断现象确实存在相关关系后，就需要进一步确定相关关系的表现形态和密切程度。在统计上，一般是通过编制相关表、绘制相关图（散点图）和计算相关系数来做出判断。根据相关表可对相关关系的表现形态和密切程度做出一般判断，依据相关系数则可做出数量上的具体分析。

3.选择合适的数学模型

确定了现象间相关关系的表现形态和密切程度后，需要选择合适的数学模型对变量之间的关系做出近似描述，进而用自变量的数值去推测因变量的数值，即所称回归分析。如果变量之间为直线相关，则采用直线模型，称为线性回归；如果变量之间为曲线相关，则采用曲线模型如双曲线、抛物线方程等，称为非线性回归。用合适的数学模型表达变量之间的关系是后续统计工作中进行判断、推算和预测的依据。

4.测定变量估计值的准确程度

在相关分析中，应用数学模型对因变量进行估值。因变量的估计值和实际值之间差异的大小表明估值的准确度，一般通过计算估计标准误差来衡量与判断。差距大则误差大，可靠程度低，差距小则误差小，可靠程度高。

5.对回归方程进行显著性检验

对建立的回归模型，要进行显著性检验，即判明变量之间是否确实存在相关关系，这种关系是否是因数据选取问题而偶然形成的。这部分内容将在8.4 节详述。