在分析社会经济现象变动时，常常需要把总指数体系和平均数指数体系结合应用，用于深入地分析社会经济现象的变动情况及其变动原因。下面仍以表7-7 为例，分析该企业销售额的增长情况及其原因。

因为工资总额＝工人总数×总平均工资

所以工资总额总指数＝工人总数指数×总平均工资指数

由于总平均工资指数是可变构成指数，则有：

即：

根据表7-7 资料，该企业工资总额的变动情况及变动的原因如下：

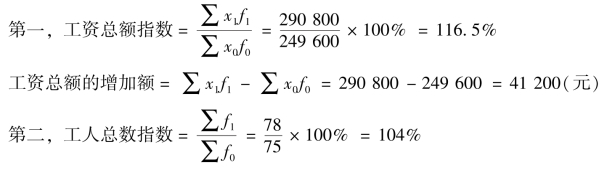
由于工人总数的增加而增加的工资总额：

由于总平均工资水平的提高而增加的工资总额：

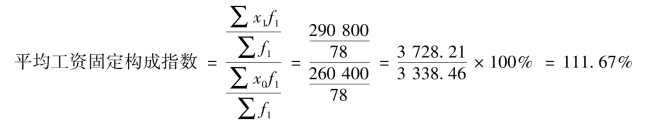
由于各组工人平均工资水平的提高而增加的工资总额：

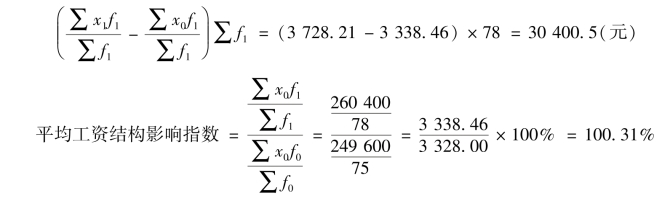
由于工人人数结构的变动，工资总额增加：

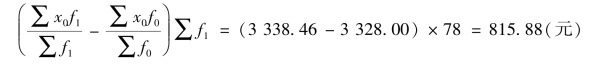
以上各指数用指数体系表示，关系如下：

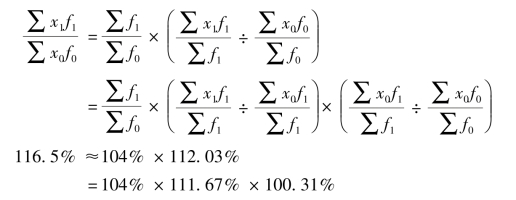
绝对数关系为：

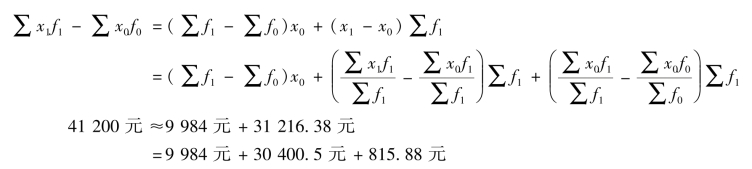(www.daowen.com)

概括分析：结果表明，该企业工资总额报告期比基期增长16.5%，是工人总数增长4%和总平均工资增长12.03%共同影响的结果。其中，该企业总平均工资报告期比基期增长12.03%，是各组平均工资增长11.67%和工人人数结构变动影响其增长0.31%的结果。

该企业工资总额增加41 200 元，一方面工人人数的增加使其增加了9 984 元，另一方面平均工资的增长使其增加了31 216.38 元。其中，因总平均工资增长而增加的31 216.38 元工资额中，各组工人平均工资水平的提高使其增加了30 400.5 元，工人人数结构的变动使其增加了815.88 元。

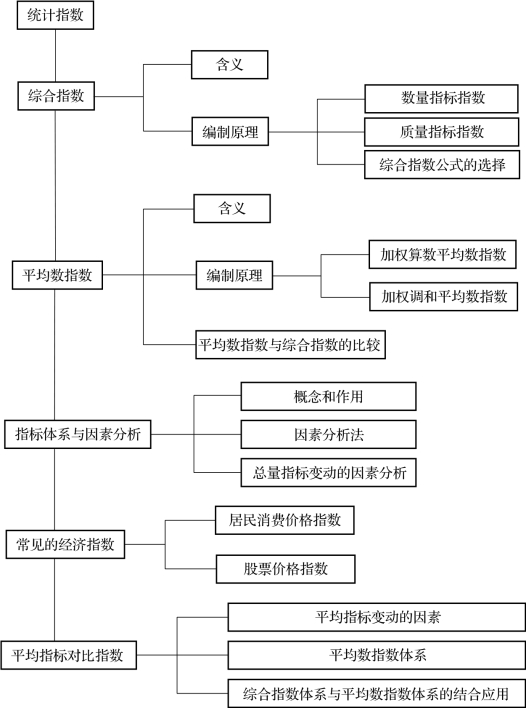
相关知识图示

本章小结

统计指数的概念有广义和狭义之分。从广义上讲，一切说明社会经济现象数量对比关系的相对数都是指数。从狭义上看，统计指数是指不能直接相加和对比的复杂现象综合变动的特殊相对数。一般来说，统计指数具有综合性、相对性和平均性的特征，即统计指数主要是用来反映和研究多种因素构成的现象的总体变动；统计指数所表明的现象的变动是相对变动；统计指数所表示的是多种现象的平均变动。

统计指数的作用主要有三方面。第一，综合反映社会经济现象总的变动方向和变动程度。第二，分析多因素影响现象的总变动中各个因素的影响大小和影响程度。第三，研究同类现象的变动趋势。

统计指数可以从不同的角度进行分类。统计指数按照说明现象的范围不同，分为个体指数和总指数；统计指数按照指数化指标的性质、内容不同，可分为数量指标指数和质量指标指数；统计指数按照指数表现形式不同，分为综合指数、平均数指数；统计指数按指数所说明的因素不同，分为两因素指数和多因素指数；统计指数按指数所反映的时间状况不同，分为动态指数和静态指数。

统计指数按其编制方法不同，可分为综合指数和平均数指数，两者都属于总指数的形式，而综合指数是总指数的最基本形式。综合指数是通过两个总量指标对比计算出来的，平均数指数则是个体指数的加权平均数。此外，在统计分析中，为了分解加权平均数中指标水平变动和单位构成两个因素的影响，而将两个不同时期同一经济内容的加权算术平均数加以对比，则形成平均数指数，其编制原理仍属综合指数。平均数指数和综合指数是计算总指数的两种形式，它们之间既有区别，又有联系。

综合指数，按其指数化指标的性质不同，可分为数量指标指数和质量指标指数两种形式。由于编制综合指数的目的是测定指数化指标的变动，因此，在对比过程中对同度量因素应加以固定。综合指数需要研究总体的全面资料，对于综合作用的同度量因素的资料要求也比较严格。有些研究对象难以取得全面资料时，可采用平均数指数法来计算总指数。

平均数指数是总指数的另一重要形式，主要有加权算术平均数指数和加权调和平均数指数两种。在每一种指数中，又由于所使用的权数不同，可再分为综合指数变形权数和固定权数两种。

在统计分析中，将三个或三个以上具有一定联系，而且具有数量上的某种对等关系的指数所构成的整体叫指数体系。利用指数体系可以对现象进行因素分析，即分析现象总变动中，各个因素的变动对总变动影响的方向和程度。利用指数体系可以进行指数间的推算。因为指数间具有数量对等关系，已知其中的其他指数，就可以推算出未知的那个指数。最后，分别介绍了居民消费价格指数和股票价格指数两种常用的价格指数的编制和应用。

指数因素分析法不仅能应用于总量指标的对比分析，还可应用于平均指标的对比分析。一般地，将两个不同时期的平均指标对比所形成的指数称为平均数指数。此外，在分析社会经济现象变动时，常常需要把总指数体系和平均数指数体系结合应用，用于深入地分析社会经济现象的变动情况及其变动原因。

思考题

1.简述统计指数的含义和作用。

2.简述因素分析的主要内容。

3.简述平均数指数和平均指标对比指数的区别。

即测即评

延伸资料